一类带非局部源项的p-Laplace方程解的整体存在与爆破
李建军,吕雅婷
(辽宁工程技术大学理学院,辽宁 阜新123000)
1.绪论及主要结论
本文研究了以下带非局部源项的p-Laplace方程解的整体存在与爆破
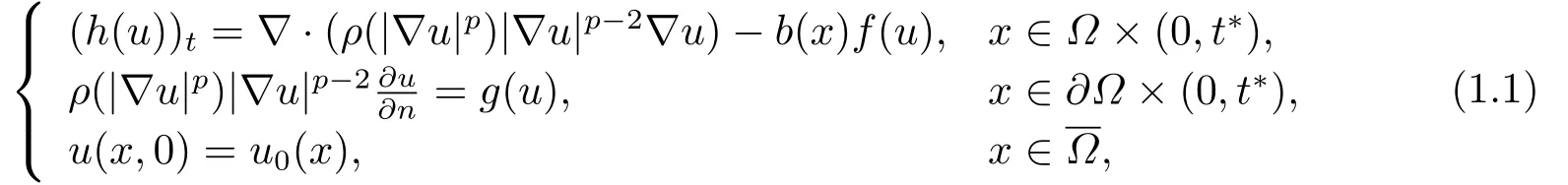
其中Ω是RN中具有光滑边界∂Ω的有界区域,n是边界∂Ω上的外法向量,u0(x)是非负函数,,当s >0 时,h′(s)>0,f,g ∈C1(R+),且f,g >0.t∗为(1.1)的解的爆破时间,即解存在的最大时间.
非线性反应扩散方程的研究涉及化学反应、传热、爆破动力学、电流变液等多个领域.在过去的几十年里,许多学者对非线性反应扩散方程(组)解的整体存在和爆破问题做了大量的研究[1–3],其中有很多作者对函数h(u)的时间导数的问题进行了研究.早在1991年,Imai和Kiyoshi[4]研究了以下拟线性退化方程
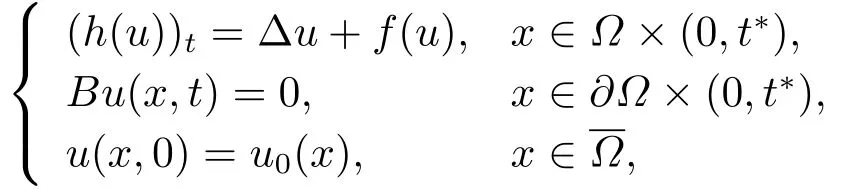
的初边值问题的爆破问题以及接近爆破时间方程解的渐近行为,其中边值条件Bu(x,t)包含Dirichlet、Neumann、Robin三种边值条件.作者对辅助函数进行假设使其满足相关条件,利用Friedman-McLeod方法来证明方程的解在有限时间内爆破.
在文[5]中,作者借用辅助函数的方法,研究了在Robin边界条件下带梯度项的非线性抛物方程解的整体存在和爆破问题,最终得到了整体解存在的充分条件和上界估计,爆破时间的上界估计和爆破速率的上界估计.文[6]的作者研究了以下带有p-Laplace方程解的整体存在和爆破问题,通过构造一些辅助函数,并且利用极值原理和微分不等式技术,证出了方程在有限时间内爆破的条件和解整体存在的条件,同时还给出爆破的上界估计.
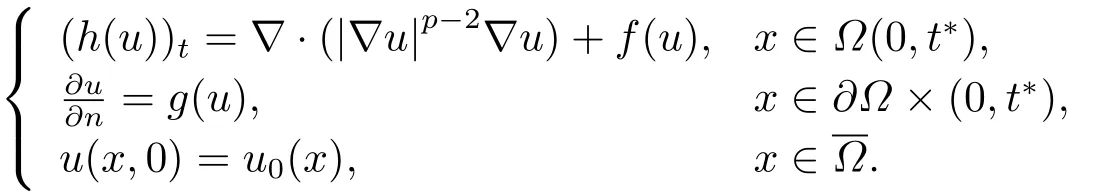
在此基础上,文[7]研究了以下带有Dirichlet边界条件的非线性反应扩散方程,通过构造辅助函数并对辅助函数中的相关参数假设,利用微分不等式技巧不仅给出了方程解整体存在的条件和解在有限时间内爆炸的结论,而且还计算了爆破时间的上下界估计.

文[8] 研究了在非局部边界条件下的p-Laplace方程的爆破问题,在微分不等式技术的帮助下,利用Soblev不等式,证明了在一定的条件下爆破解的存在.并且还得到了爆破时间的上界和下界估计.赵阳洋和崔泽建[9]研究了当问题(1.1)中的参数p=2时,方程解的整体存在性和爆破性,并给出了爆破时间的上下界估计.
受到以上文献的启发,本文对问题(1.1)解的整体存在性和爆破性进行研究.通过构造不同的辅助函数,利用Young不等式、Sobolev不等式等微分不等式来证明解整体存在和爆破.
2.解的整体存在性
在本节中主要的研究内容为问题(1.1)解的整体存在性.为了证明方程解的整体存在性,需要建立如下辅助函数:

先给出本节的主要结论:
定理2.1设u是方程(1.1)的非负古典解,并且满足
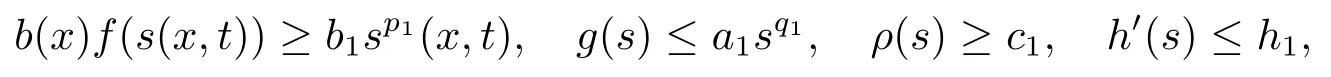
证将函数Φ(t)对时间t求导,得到
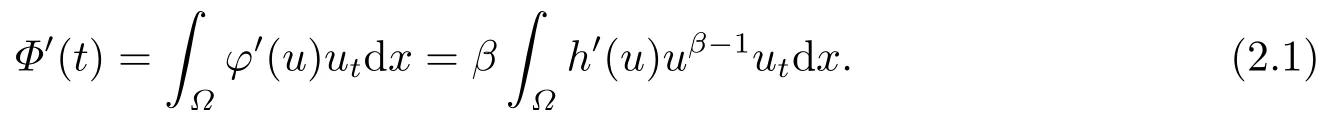
由定理2.1中的相关条件,将问题(1.1)的第一个式子代入(2.1)中,则有
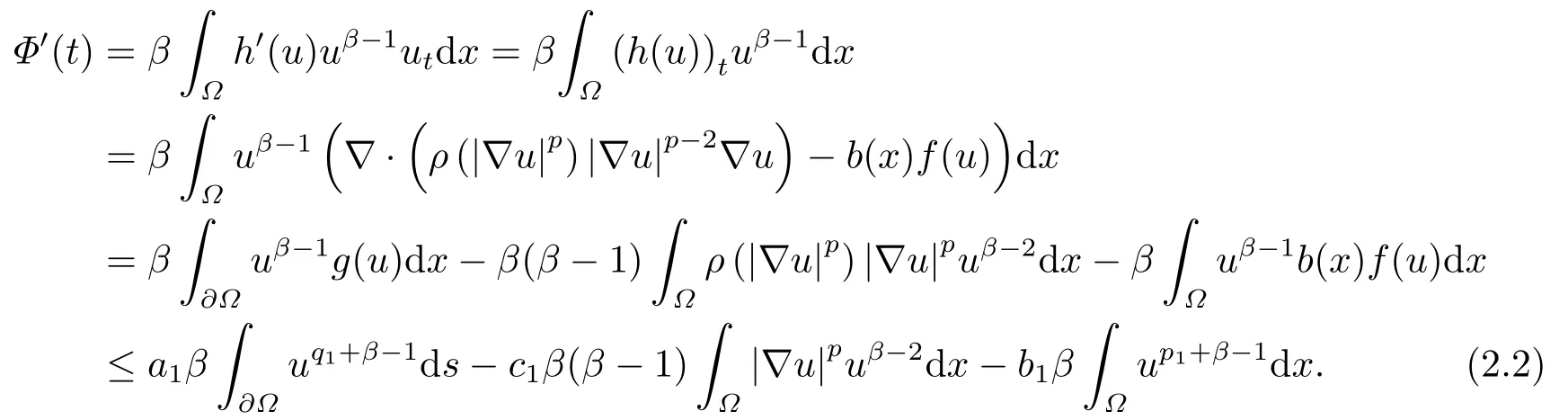
由散度定理[10],可知式(2.2)的右端第一项有:

接下来利用微分不等式技巧对式(2.3)右端的两项进行分析.将(2.3)右边的第一项和第二项利用Young不等式
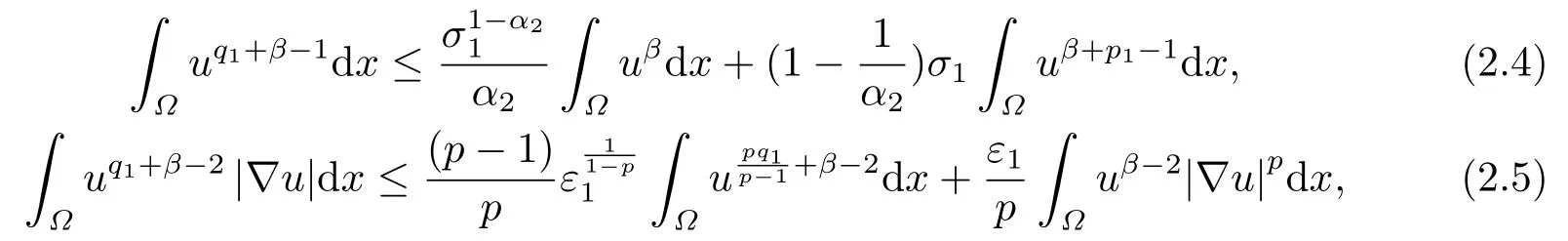
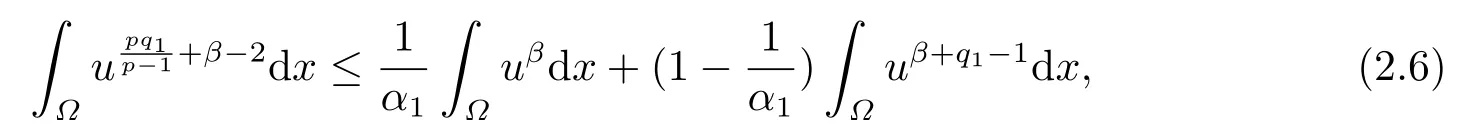

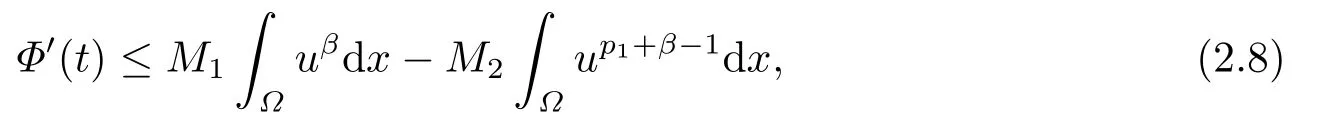
其中
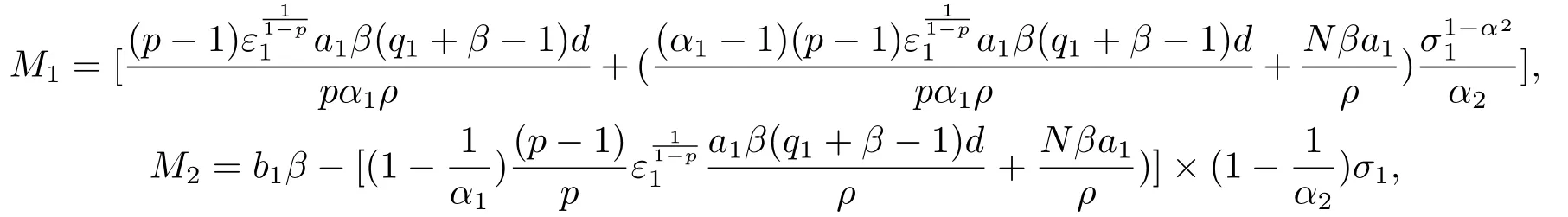
且M1>0,取
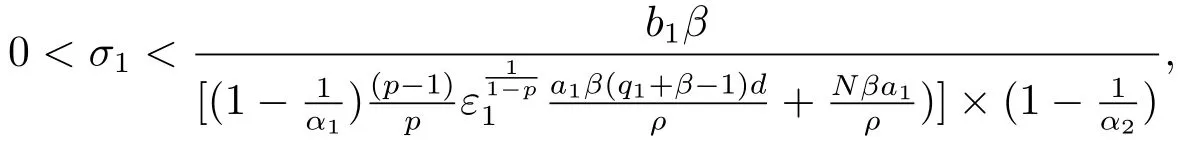
使得M2>0.
由Hölder不等式,有
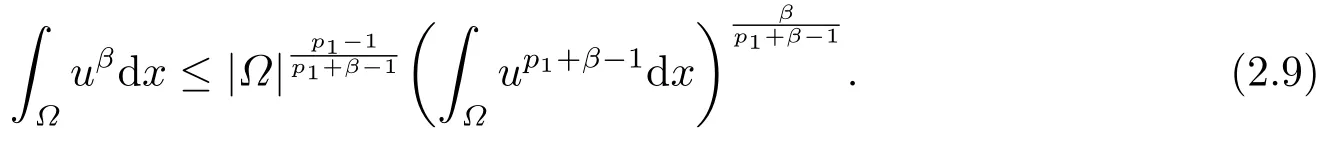
对上式进行变换,可得

将式(2.9)带入式(2.8),可得
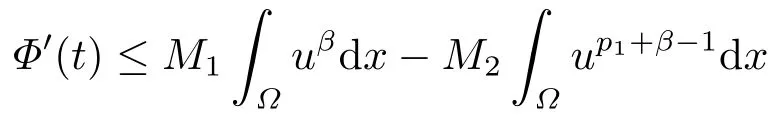
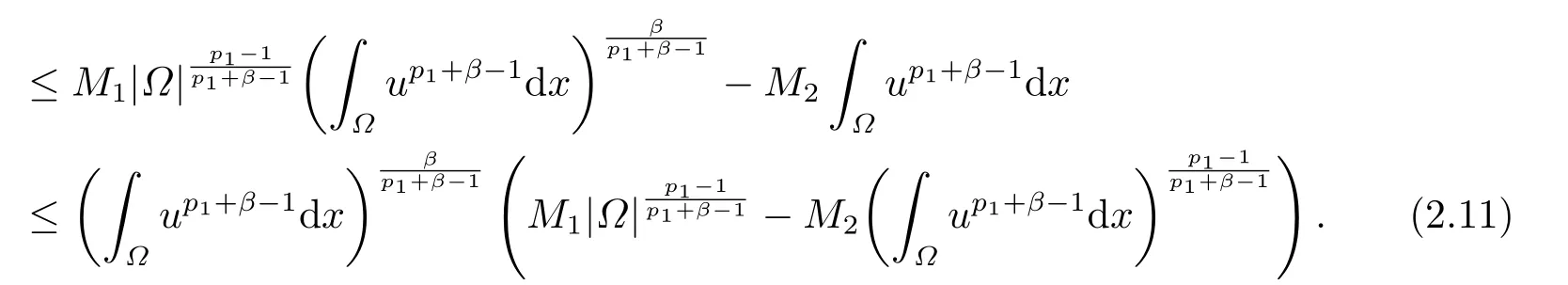
由定理2.1中的假设条件对辅助函数进行估计
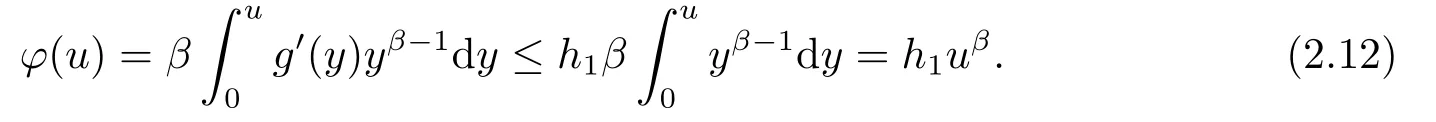
对式(2.12)两端求积分,可得

即

结合式(2.10)、(2.11)、(2.13),计算可得
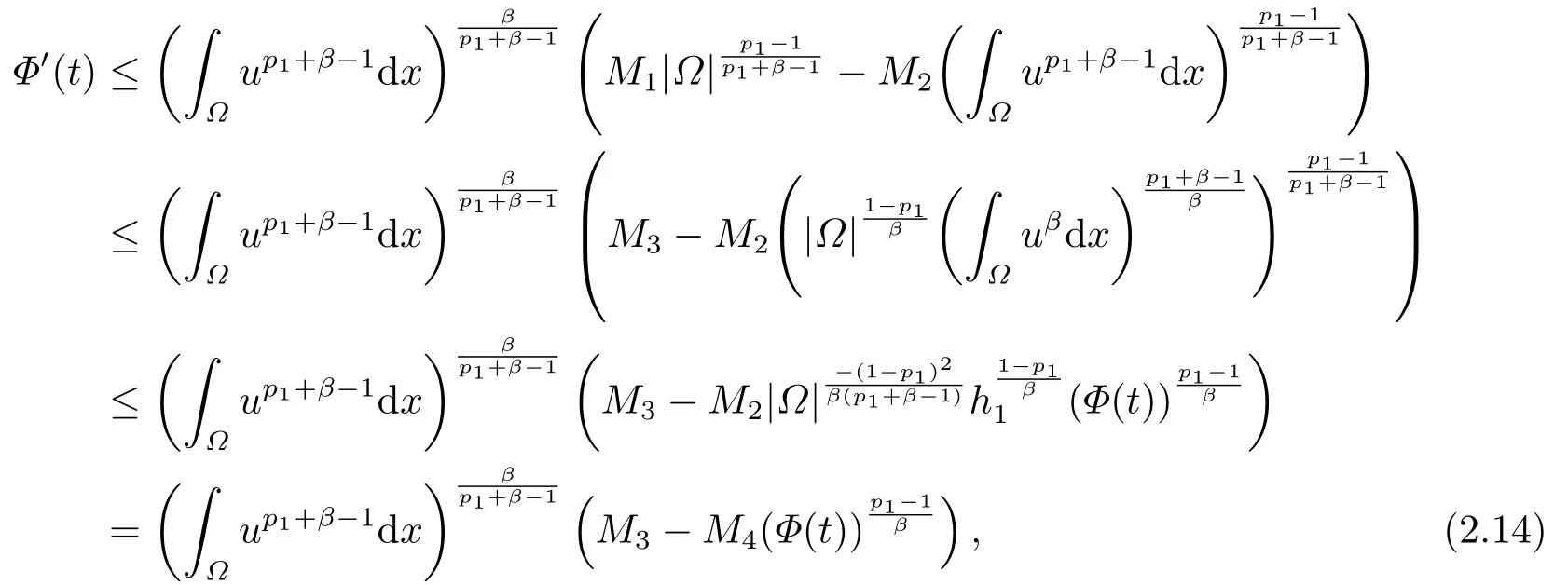
接下来,我们利用反证法来证明定理2.1的成立.假设以上的结论是错的,即一定存在时间t∗使得函数在函数Φ(t)的意义下爆破,即
令t →t∗−,可以得到所以,一定存在一个时间t1 对上式两边取极限,即令时间t →t∗−,我们可以得到以下不等式 这与结论产生矛盾,所以定理2.1成立. 本节的主要内容是方程(1.1)的解在有限时刻爆破的充分条件以及解爆破时间的上界估计.为了得到结果,第2节给出的辅助函数已经不能继续使用,需要重新构造如下的辅助函数: 先给出本节的主要结论: 定理3.1设u是方程(1.1)的非负古典解,并且满足 且初始值Ψ(0),Φ1(0)>0,则方程(1.1)的解u在函数Φ1(t)的意义下在有限时间爆破,当p >2,时,Φ1(t)→∞;当0 接下来证明方程(1.1)的解u在函数Φ1(t)的意义下爆破. 证对辅助函数Φ1(t)关于时间t进行求导,则可以得到下式 根据定理3.1中的相关条件,将式(1.1)的第一个式子带入式(3.1)中,则上式为 再对辅助函数Ψ(t)关于时间t进行求导,则有 利用分部积分对辅助函数H(u)进行分析,可得 结合式(3.3)和式(3.4)以及Hölder不等式可得不等式 也就是说 将不等式(3.6),从0到t进行积分,有 将式(3.2)带入上式,可得 1)当p>2时,将(3.7),从0到t进行积分,得到 2)当0 本节的主要内容为问题(1.1)的解爆破时间的下界估计.为了得到本节的研究内容建立如下的辅助函数: 在证明结论之前,先给出本节的主要结论: 定理4.1假设u是方程(1.1)的非负古典解,且在t∗处爆破,函数满足 其中,r1,r2,r3,r4由(4.17)-(4.20)给出. 为了得到方程(1.1)的解爆破时间的下界估计,我们利用下面两个不等式: 由文[11]中推论9.14,可以得到当N >2时,则有下列Sobolev不等式 证将函数Φ2(t)对时间t求导,得到 根据定理4.1中给出的假设条件,上式为 将式(4.6)带入式(4.4)中,则有 下面重复过程(2.3)、(2.5)、(2.6),可得如下不等式 其中C是Sobolev指数,且依赖于N和Ω的值.由Young不等式计算(4.10)等式右边第二项可得 其中ε3待定.利用Young不等式对(4.10)右端第一项进行估计 其中ε4待定,在后面会给出具体的数值.结合式(4.7)-(4.13),得到 接下来将函数积分项转化成辅助函数Φ2(t)的指数形式.由定理4.1中的条件计算可得 即 将ε1,ε2,ε3,以及式(4.15)代入(4.14)中,可得 其中 如果方程(1.1)的解在函数Φ2(t)意义下有限时间爆破,即,对式(3.37)关于时间t在[0,t∗]上进行积分,整理后可得 本节通过几个例子来说明定理2.1-4.1的结果. 例5.1设u(x,t)是下列方程的非负古典解: 其中Ω ⊂R3,且Ω是一个单位球,h(u)=,f(u)=u3,p=4.通过对例5.1的分析,可知定理2.1中的假设条件方程(5.1)满足,取β=3,则函数Φ(t)为 由定理2.1可知,例5.1中方程的解在函数Φ(t)的意义下整体存在. 例5.2设u(x,t)是下列方程的非负古典解: 其中Ω ⊂R3,Ω是一个半径为0.5的球. 分析式(5.2),有 下面计算各个辅助函数: 通过以上的计算,很显然,定理3.1中的假设条件满足,所以 所以,由定理3.1可知方程(5.2)的解的爆破时间上界为: 例5.3设u(x,t)是下列方程的非负古典解: 其中Ω ⊂R3,且Ω是一个单位球,|∂Ω|= 4π,h(u)=u+ln(u+1),ρ(∇u|4)= e|∇u|4,g(u)= eu2,b(x)f(u)= 由定理4.1,可知a2= e,b2= 0.5,p2= 3,q2= 2,c2= 1,m= 1,h2= 1,β1= 4,d0= 1,ρ0= 1通过查询文[12],可以得到Sobolev指数C= 7.5931.很容易可以计算得到上述参数满足定理4.2的条件,则 由定理4.1,可以得到若解发生爆破时方程的解爆破时间的下界为 本文通过构造辅助函数,以及微分不等式得出问题(1.1)解整体存在和爆破解的充分条件,以及方程解的爆破时间上界和下界的估计,并通过三个具体的例子进行说明.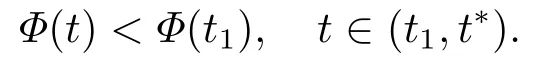
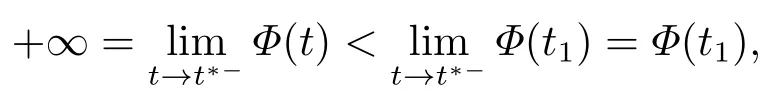
3.解爆破时间的上界估计

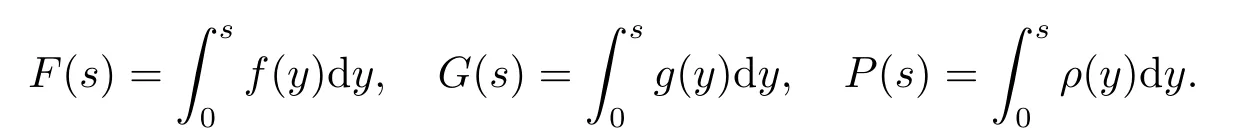
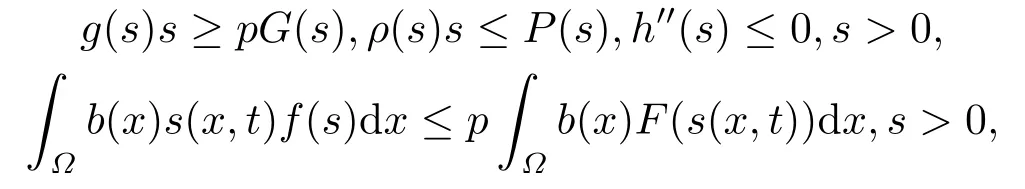
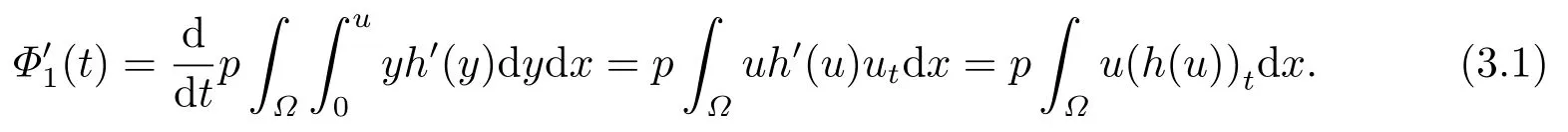

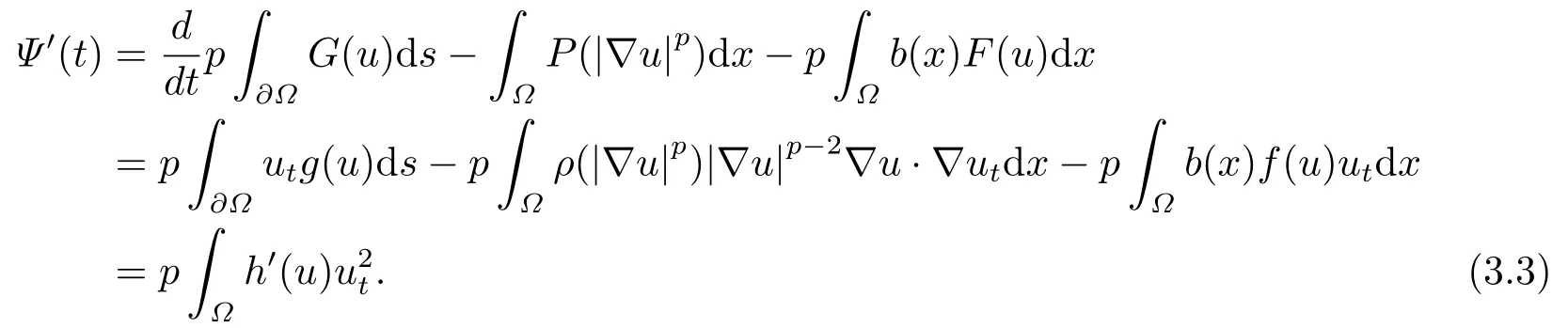

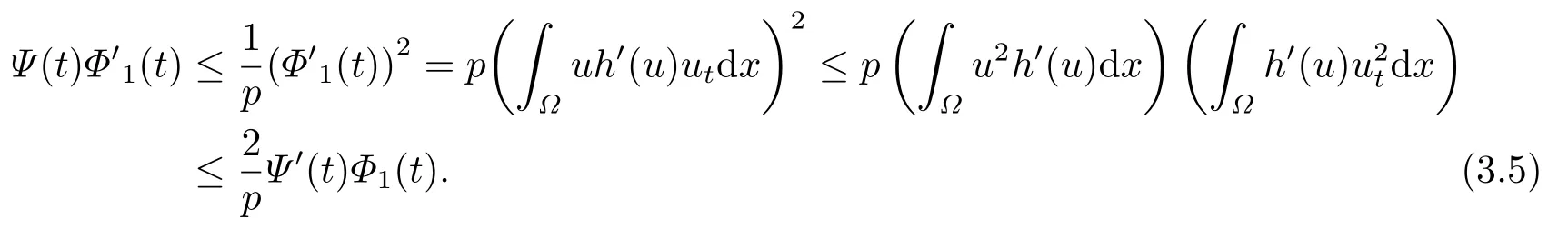

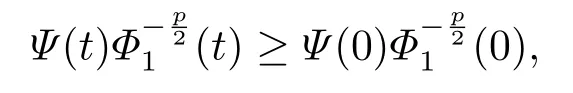


4.解爆破时间的下界估计
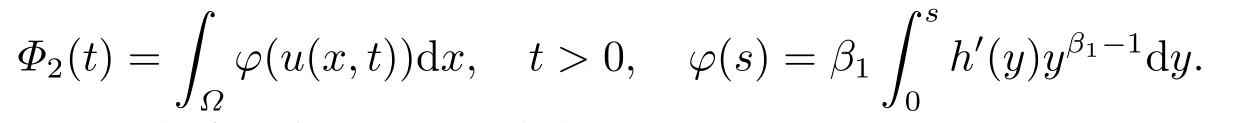
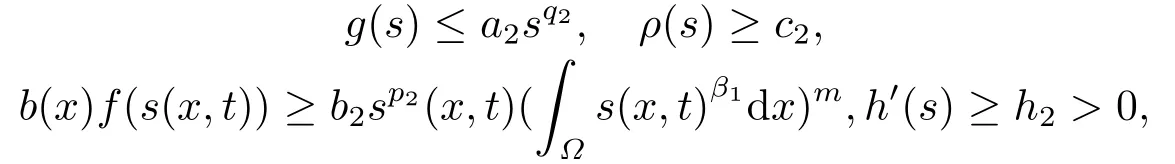


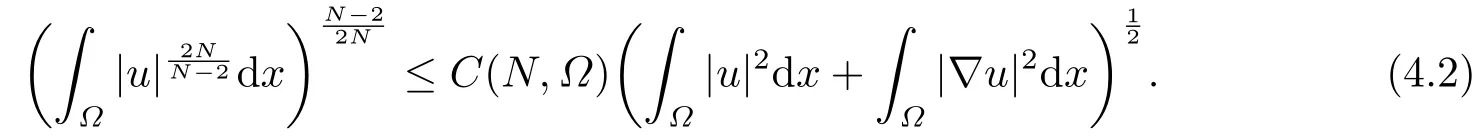
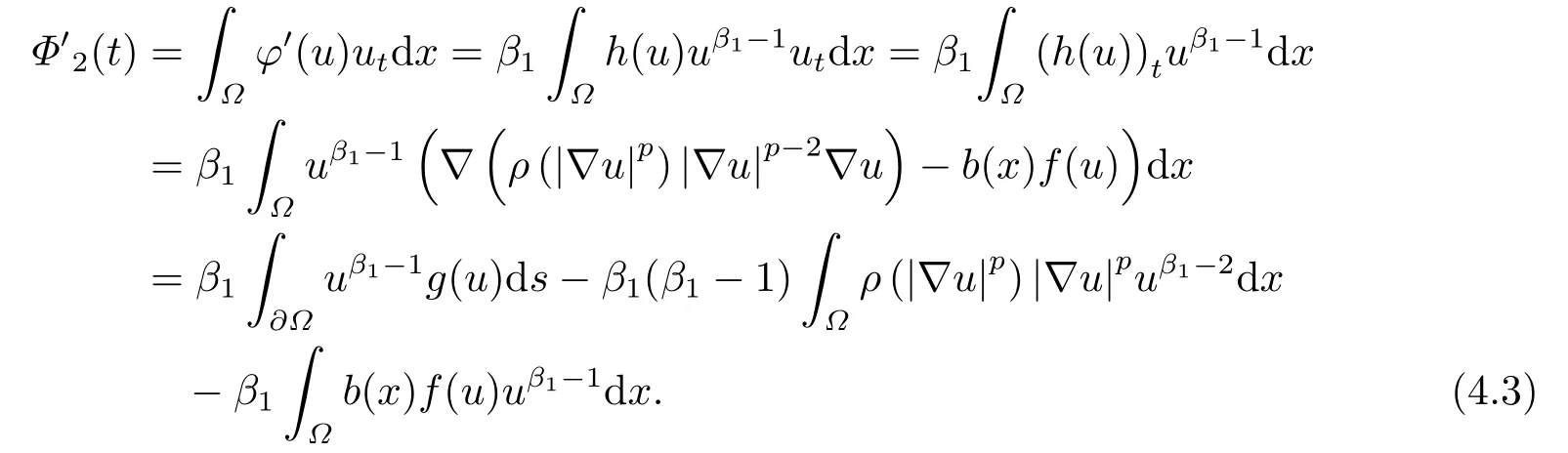



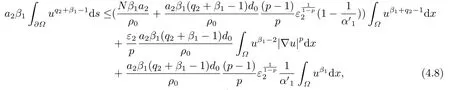

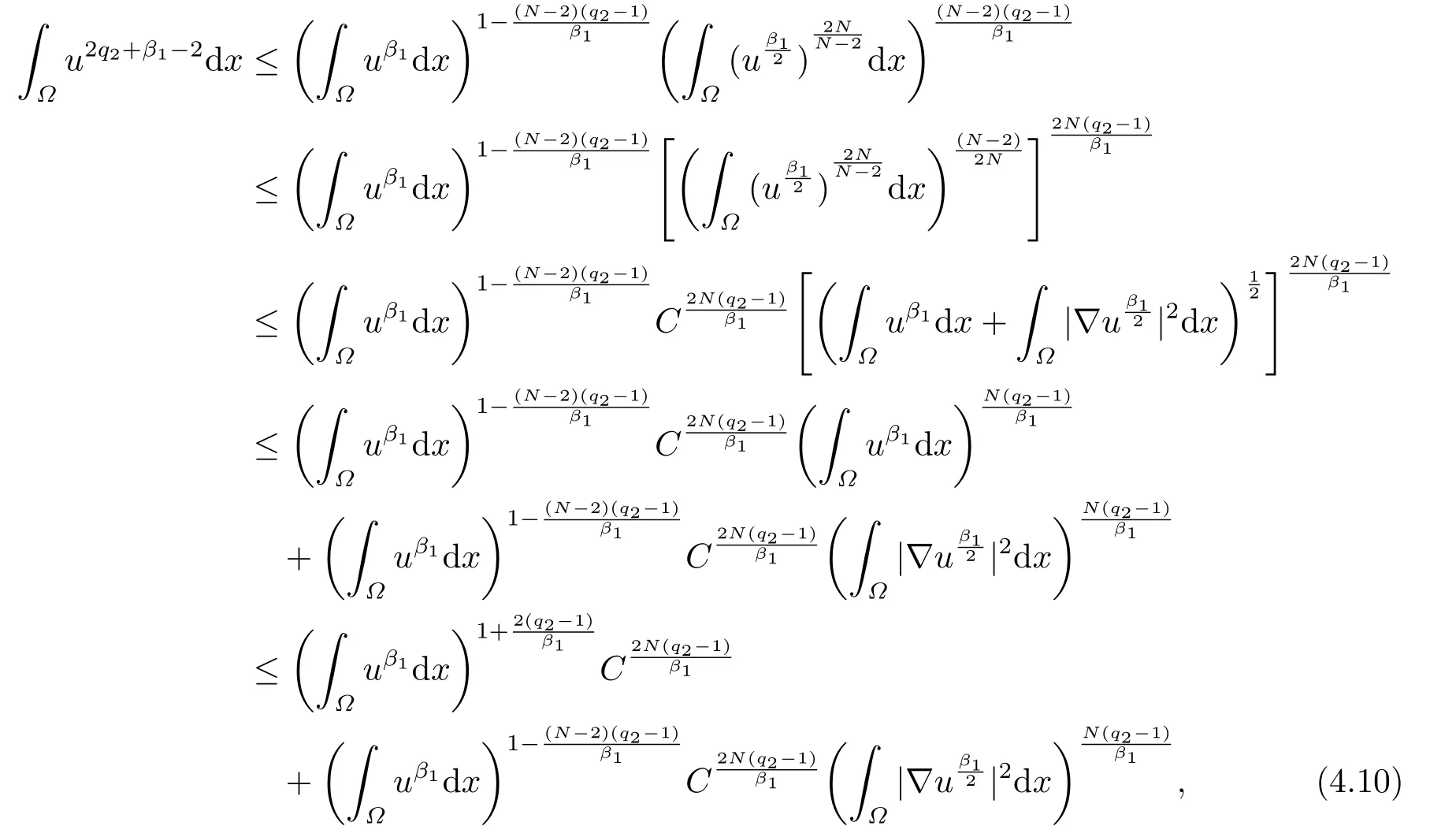

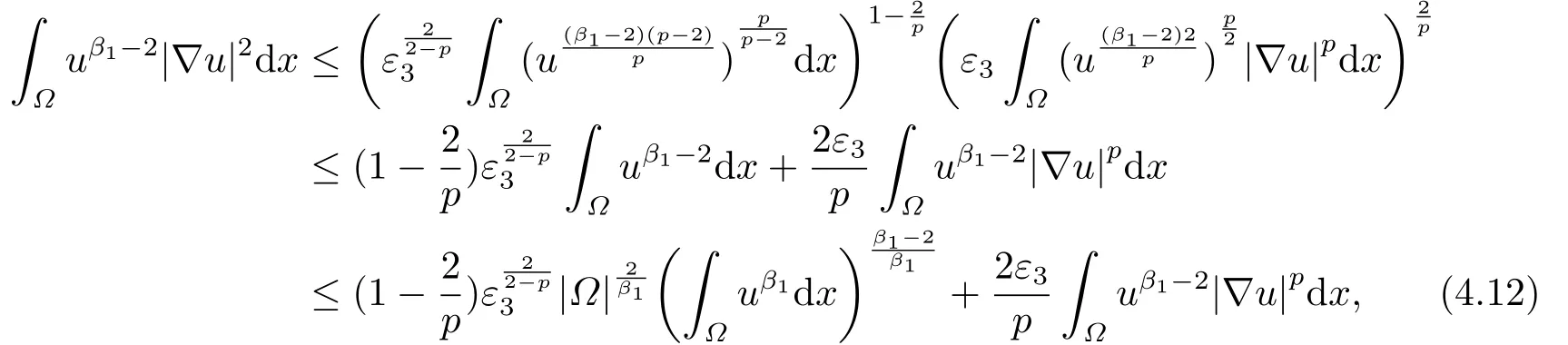


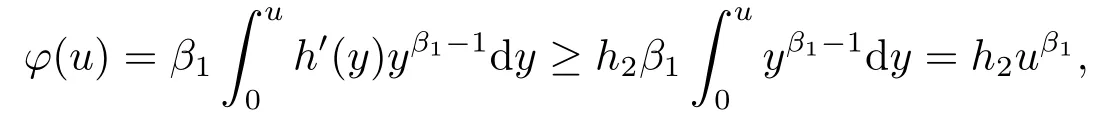

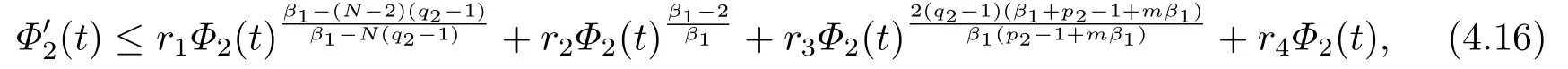

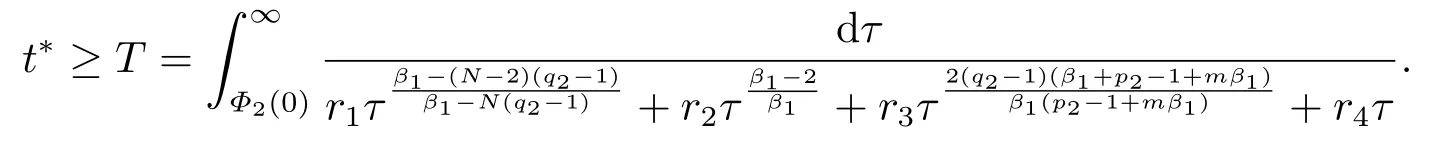
5.应用

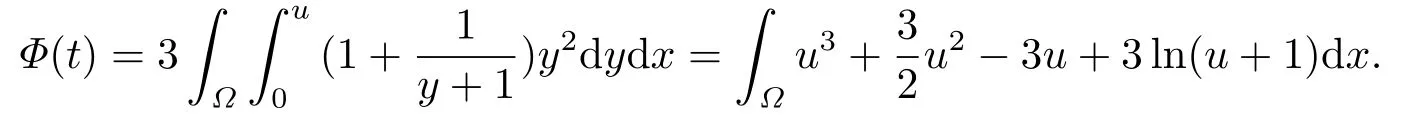

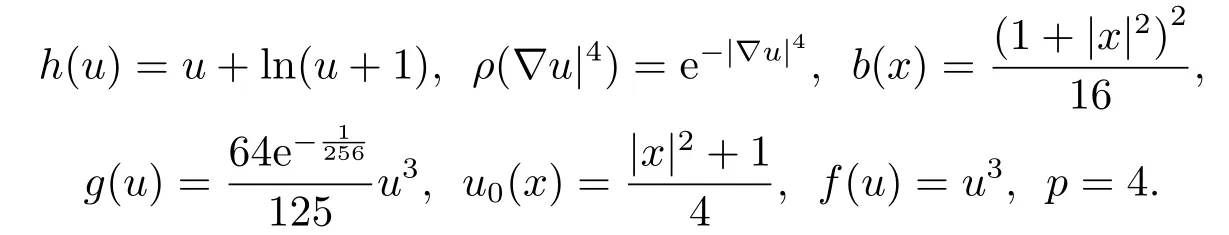
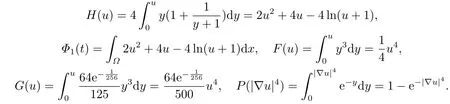

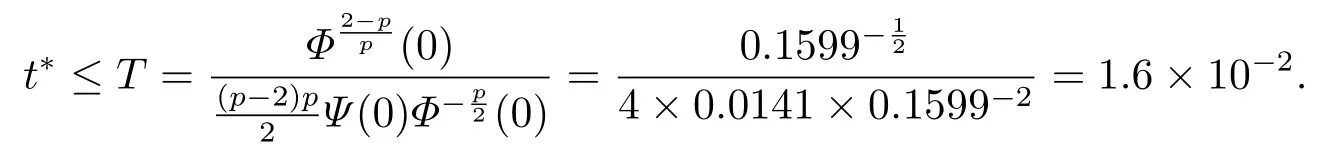
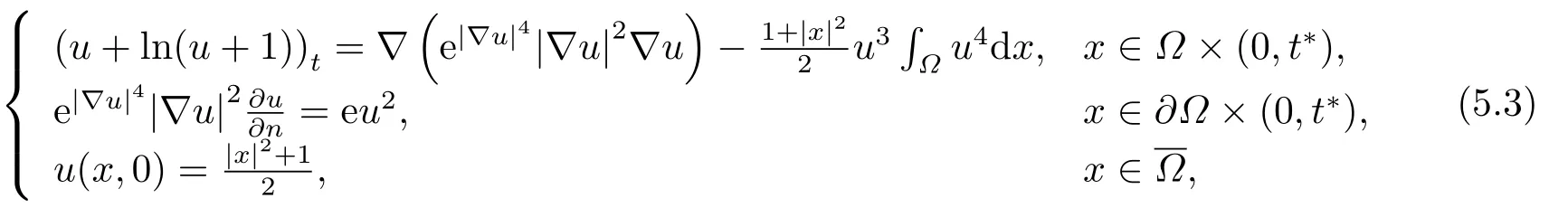


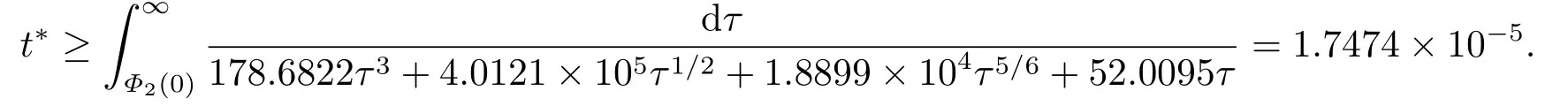
6.总结

