数学命题教学中的问题链设计
任燕巧


摘要:数学命题教学可以利用数学问题链,引导学生充分经历数学命题的探究发现过程,同时,体会其中的数学思想方法,发展数学核心素养。具体设计问题链时,应该注意从猜想到证明、从特殊到一般(有时还包括从直观到抽象)、从发现到应用的一般研究过程。此外,还应特别关注有关概念和命题及其形成和发现过程中可以類比迁移的重要思想方法,助力学生猜想和证明结论。以“平面与平面平行的判定定理”教学的问题链设计为例来说明。
关键词:数学命题教学;问题链设计;面面平行的判定定理
数学命题(包括定理、公式等结论)是数学知识的重要组成,是数学思维的重要节点。自然地,数学命题教学是数学教学的重要类型。同为数学知识教学,数学命题教学与数学概念教学类似,也存在“一个结论(对数学概念教学而言,是一个定义),几点注意,大量练习”的现象。这样的教学忽视了命题的探究发现过程,直接影响了学生对命题的完整认知和深度理解。
数学问题链是教师在课外预设并在课上以多种方式呈现给学生的、有序的主干数学问题序列,可以驱动学生的数学探究,体现数学思维的脉络。数学命题教学可以利用数学问题链,引导学生充分经历数学命题的探究发现过程,同时,体会其中的数学思想方法,发展数学核心素养。具体设计问题链时,应该注意从猜想到证明、从特殊到一般(有时还包括从直观到抽象)、从发现到应用的一般研究过程。此外,还应特别关注有关概念和命题及其形成和发现过程中可以类比迁移的重要思想方法,助力学生猜想和证明结论。
下面,以“平面与平面平行的判定定理”教学的问题链设计为例来说明。
一、总体教学思路
“平面与平面平行的判定定理”是人教A版高中数学教材(2019年版)必修第二册“8.5.3平面与平面平行”中的内容。教学这一内容时,除了体现从猜想到证明再到应用、从特殊平面(比如长方体中的平面)到一般平面、从直观(实物)到抽象(模型)的基本研究框架之外,分析知识的前后关联以及学生的学习困难可知,还要引导学生类比迁移直线与平面平行判定定理发现过程中的降维转化思想和反证法,猜想和证明平面与平面平行的判定定理;并且,特别注意引导学生运用平面与平面平行的判定定理,寻找与已知平面平行的平面。
二、具体问题链设计
问题1如图1,正方体ABCDA1B1C1D1中,E为DD1的中点,判断BD1与平面AEC的位置关系?你的依据是什么?
问题1旨在唤醒学生对线面平行判定定理(方法)的记忆:连接BD,交AC于O,连接OE,通过面外线BD1与面内线OE平行证明线面平行。对此,引导学生体会把线面平行问题转化为线线平行问题过程中的降维思想。进而,引导学生回顾依据定义和判定定理判定线面平行这两种方法,并且体会判定定理方法的便捷性。这是学生后续类比探究面面平行判定定理的基础。
问题2如果要判定平面α与平面β平行,你会怎么想?
问题2是一个开放性问题,旨在激活学生对面面平行判定定理(方法)的猜想。课堂上,学生结合已有经验,借助长方体模型,类比线面平行判定定理的猜想,首先指出了定义方法(判定两个平面没有公共点)操作上的麻烦;接着想到了将面面平行问题降维转化为线面平行问题的方法,提出了“若一个平面内的一条直线与另一个平面平行,则这两个平面平行”的猜想;之后又发散思维,提出了“垂直于同一条直线的两个平面平行”“平行于同一个平面的两个平面平行”等猜想。
对此,教师肯定了降维转化的思路,同时引导学生结合长方体模型,否定了“若一个平面内的一条直线与另一个平面平行,则这两个平面平行”的猜想;肯定了“垂直于同一条直线的两个平面平行”“平行于同一个平面的两个平面平行”等猜想的正确性,同时指出线面垂直的判定方法还没有学习,面面平行的判定正是目前需要解决的问题,从而否定了这两个猜想作为面面平行判定定理的合理性。由此,自然引出问题3。
问题3类比线面平行判定定理的猜想,要把面面平行问题降维转化为线面平行问题,该如何操作?
问题3是一个聚焦性问题,旨在明确学生对面面平行判定定理(方法)的猜想。课堂上,学生在否定“若一个平面内的一条直线与另一个平面平行,则这两个平面平行”猜想的基础上,自然联想提出了“若一个平面内的两条直线与另一个平面平行,则这两个平面平行”的猜想。由此,教师分平行和相交两种情况,提出了两个子问题:
问题31如图2,矩形硬纸片两条对边所在直线a、b与桌面平行,矩形硬纸片所在平面与桌面平行吗?
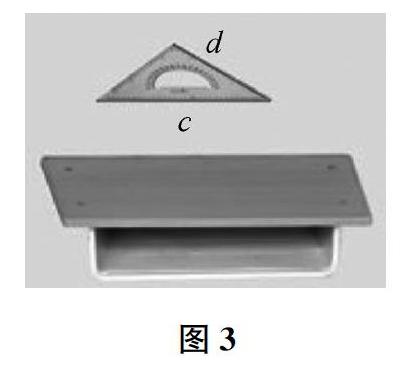
问题32如图3,三角尺两边所在直线c、d与桌面平行,三角尺所在平面与桌面平行吗?
这两个子问题旨在引导学生通过观察实物,获得对面面平行判定定理(方法)充分的直观感知,明确提出“若一个平面内的两条相交直线与另一个平面平行,则这两个平面平行”的猜想。
问题4如图4,请证明:若平面β内的两条相交直线a、b与平面α平行,那么α与β平行。
问题41如图5,你能结合长方体模型证明上述结论吗?
有了猜想,问题4自然要求学生证明面面平行的判定定理(方法)。当然,学生即使类比线面平行判定定理的证明,想到反证法,实际证明也会感到困难。因此,设计了问题41这个辅助性的子问题,让学生借助长方体模型,尝试证明上底面内的两条相交直线与下底面平行时上下两个底面平行。由此深化,学生能借助图6,完成一般情况的证明。
问题5面面平行的判定是通过将面面平行降维转化为线面平行来解决的,那么是否存在进一步降维转化为线线平行的方法呢?
问题5是对问题3的进一步延伸,即进一步把面面平行问题降维转化为线线平行问题来探讨,可以引导学生得到面面平行判定定理的推论;也是对问题4探究过程,即线面平行情况证明过程中所使用的思路与方法的进一步应用与巩固,因为这里如何寻找可以用来判定面面平行的直线、如何借助反证法证明等问题的解决过程都与问题4中的一致。
问题6判断对错,并说明原因。
(1)如果一个平面内有两条直线平行于另一个平面,那么这两个平面平行。
(2)如果一个平面内有无数条直线平行于另一个平面,那么这两个平面平行。
(3)如果一个平面内任意一条直线平行于另一个平面,那么这两个平面平行。
问题7如图7,现实生活中,建筑工人、木工师傅等会将气泡式水平仪在桌面上交叉放置两次,通过水平仪的气泡是否都在中央,判定桌面与水平面是否平行。你能解释其背后的数学原理吗?
问题6是对面面平行判定定理条件的进一步辨析,帮助学生把握面面平行判定定理的本质。问题7是面面平行判定定理的实际应用,引导学生运用面面平行的判定定理解释生活现象,体会数学与生活的联系,提高解决问题的能力。
问题8如图8,已知正方体ABCDA1B1C1D1,求证:平面B1AD1∥平面BC1D。
问题9如图9,已知正方体ABCDA1B1C1D1,点E、F、M分别为A1B1、AA1、B1C1的中点。在此正方体中,是否存在过点E、M且与平面BFD1平行的平面?若存在,请作出并证明;若不存在,请说明理由。
问题8是面面平行判定定理的直接应用,引导学生运用面面平行的判定定理及推论证明数学结论,体会定理运用的关键,掌握规范的解题过程。问题9引导学生运用面面平行的判定定理,寻找与已知平面平行的平面(结合已知条件,这里还需找到一个点,可取BB1靠近B1的一个四等分点),然后证明,具有开放探索性,是学生学习的难点。此题需要留给学生足够的思考时间,帮助学生形成完整、清晰的解题思路。
问题10平面与平面平行有哪些判定方法?这些方法之间有什么联系?我们已经知道平面与平面平行的判定方法,反之,还能研究什么?
问题10对本节课的回顾总结与拓展延伸,可以引导学生回顾面面平行的判定定理,体会类比迁移、降维转化的思想方法和“猜想—证明—应用”的研究过程,并进一步体会“判定—性质”的研究拓展。
三、几点教学反思
纵观本节课的教学,有这样几个特点:
(一)层层递进,给予脉络化思考
问题链中的主干问题是有序的、层进的,不仅能够驱动学生探究,而且能够引导学生体会数学思维的脉络。本节课中,问题1为学生类比迁移探索线面平行判定定理的思路与方法提供了支架;问题2—问题5引导学生经历猜想的自由发散与合理聚焦、证明的严谨推理与深化推论,体验定理及推论的发现过程;问题6—问题9引导学生体验定理及推论的各类应用,真正获得完整认知和深度理解;问题10则是对全课的总结延伸。层层递进的问题给予学生脉络化的思考,促进学生掌握解决一类问题、学习一类知识的基本框架。
(二)直观感知,赋予情境性理解
美国著名教育心理学家布鲁纳说过,当基本概念以正规形式出现在儿童面前时,他们如果没有事先从直觉上加以理解,对这些概念则将无能为力。本节课中,问题31、问题32、问题41等子问题从实物到长方体模型,为探究抽象的一般性问题提供直观感知的基础,帮助学生形成情境性理解。
(三)留有余地,指向深度的学习
数学教学要设置具有一定挑战性的问题,为学生的思考留有余地(空间),激发学生的探究欲望,发展学生高水平的数学思考。本节课中,有关定理猜想、证明、应用的问题2、问题4、问题9便是如此,学生在思考中很容易出现错误、缺憾、求而不得、悬而未决等情况。相应的教学处理则是延迟解决,促使学生努力寻求解决方案,得到完整、清晰的思路,实现深度学习。
*本文系全国教育科学规划课题教育部重点课题“指向深度理解的‘问题链教学研究”(编号:DHA200318)的阶段性研究成果。
参考文献:
[1] 唐恒鈞,黄辉.数学问题链教学设计与实施的三个关键[J].中学数学,2020(5).
[2] 周丕芬.类比为桥自然生成——“平面向量的实际背景及基本概念”教学设计、实践与反思[J].中学数学教学参考,2020(1/2).
[3] 丁益民.以立体几何教学为例谈理性精神的培育[J].教育研究与评论(中学教育教学),2019(10).

