凸多面体不确定Delta算子切换系统的二次D-稳定性*
李 娟,肖民卿,王佑恩
(1. 福建师范大学 数学与信息学院, 福建 福州 350007;2. 三明学院 信息工程学院, 福建 三明 365004)
近年来,Delta算子理论在自动控制和信号处理等方面起着越来越重要的作用.Delta算子方法[1]克服了高速采样时前向位移算子引起的数值不稳定问题,并且当采样周期趋于零时,Delta算子系统的模型参数趋于相应的连续时间模型参数,因此,Delta算子离散化方法能够统一处理连续和离散时间系统的控制问题.
另一方面,切换系统能够有效地描述许多由单一模型无法刻画的复杂系统,故其应用领域越来越广[2].典型的切换系统是由一组连续(或离散)时间子系统和一组决定子系统间如何切换的切换规则组成的.许多实际的系统,例如大规模电力系统、计算机控制系统,都可以用切换系统建模.目前,在切换系统的稳定性、控制器设计等方面,已有学者取得了成果[3,4].
在实际的工程控制中,为达到期望的控制效果,不仅要求系统具有较好的稳态特性,还需要良好的暂态性能.由于模型的不确定性和各种扰动的存在,将闭环系统的极点配置在复平面上的一个适当区域内,就可以确保闭环系统的暂态响应[5].若线性时不变系统的极点都落在稳定域内指定的圆形区域中,则称该系统是D-稳定的[6].国内外学者对在系统D-稳定性下的控制问题的研究已经有了大量的成果.文献[7]研究了Delta算子系统的D-稳定可靠控制.文献[8]研究了线性切换系统的D-稳定性.文献[9]研究了Delta算子切换系统的非脆弱可靠D-稳定问题.文献[10]通过算例验证了将切换系统子系统的极点约束在稳定域的圆盘内时,系统的收敛速度变快,振荡的次数与幅度也会变小.因此,子系统的极点约束对于切换系统而言,具有重要的理论意义和实践价值.关于由多面体不确定子系统组成的切换系统的二次稳定问题,考虑到大多数不确定控制系统都可以用多面体不确定性系统来近似,翟[11]等人通过状态反馈实现了由多面体不确定子系统组成的连续时间和离散时间切换系统的二次稳定.
本文基于Lyapunov二次稳定的方法,研究了不确定Delta算子切换系统的二次D-稳定问题.给出了不确定Delta算子切换系统在状态依赖切换律下的二次可稳定的充分条件,同时将系统的极点配置在给定的圆盘区域内.
符号说明:上标T表示矩阵的转置.T为离散化采样周期.W>0(<0)表示W是对称正(负)定矩阵,W1>W2即W1-W2>0.W≥0(≤0)表示W是对称半正(负)定矩阵,W1≥W2即W1-W2≥0.I是单位矩阵.
1 问题描述
考虑下述不确定Delta算子切换系统模型:
δx(t)=Aσ(t)x(t),
(1)
其中t=kT,k=0, 1, 2, …,T,为采样周期,x(t)∈n是n维状态向量(初始状态x(0)=x0),σ(x,t):n×T→{1,2} (T={0,T, 2T, 3T, …}) 是系统的切换律, 在后面将会给出定义.Delta算子(或δ算子)的定义如下:
其中T为离散化采样周期, 当T=0时系统为连续时间系统,当T≠0时为离散系统.Delta算子和前向位移算子q之间的关系为:δ=(q-1)/T,T≠0.

Delta算子切换系统(1)是由下面两个子系统组成的:
δx(t)=A1x(t),
(2)
δx(t)=A2x(t).
(3)
本文考虑子系统(2)和(3)是凸多面体描述的不确定系统, 具体定义如下:
(4)
其中, 凸多面体Ωi的顶点Aij为n阶常数矩阵,j=1,2,…,Ni,Ni是凸多面体Ωi的顶点个数.
下面给出系统二次稳定的定义, 以及在证明中需要用到的结论.

δV(x)<-εxTx
成立, 则称不确定Delta算子切换系统(1)是状态依赖二次D-可稳定的.
引理1(Cauchy不等式)
等号成立的充分必要条件是向量(a1,a2, …,an)与(b1,b2, …,bn)线性相关.
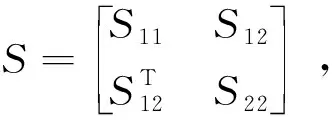
(1)S<0;


2 主要结论

λij[(A1i-αI)TP(A1i-αI)-r2P]+(1-λij)[(A2j-αI)TP(A2j-αI)-r2P]<0,
i=1, 2, …,N1,j=1, 2, …,N2;
(5)
(A1k-αI)TP(A1l-αI)+(A1l-αI)TP(A1k-αI)-2r2P≤0,
k,l=1,2,…,N1,k≠l;
(6)
(A2u-αI)TP(A2v-αI)+(A2v-αI)TP(A2u-αI)-2r2P≤0,
u,v=1,2,…,N2,u≠v,
(7)
成立, 则不确定Delta算子切换系统(1)是状态依赖二次D-可稳定的.
证明由不等式(5)可知, 存在正标量ε0使得
λij[(A1i-αI)TP(A1i-αI)-r2P]+
(1-λij)[(A2j-αI)TP(A2j-αI)-r2P]<-ε0I.
(8)
于是, 由不等式(8)可知, 对系统的状态x(t)有
λijxT(t)[(A1i-αI)TP(A1i-αI)-r2P]x(t)+
(1-λij)xT(t)[(A2j-αI)TP(A2j-αI)-r2P]x(t)<-ε0xT(t)x(t).
(9)
由于0≤λij≤1, 因此若有某个i0∈{1, 2, …,N1}, 使得
xT(t)[(A1i0-αI)TP(A1i0-αI)-r2P]x(t)≥-ε0xT(t)x(t),
则由(9)知,λi0j≠1,j=1,2,…,N2, 且
(1-λi0j)xT(t)[(A2j-αI)TP(A2j-αI)-r2P]x(t)<
-(1-λi0j)ε0xT(t)x(t),j=1, 2, …,N2.
因此
xT(t)[(A2j-αI)TP(A2j-αI)-r2P]x(t)<-ε0xT(t)x(t),j=1, 2, …,N2.
所以, 下列两个不等式组(10)和(11)至少有一个成立:
(10)
(11)
又由不等式(6)可以得到
xT(t)[(A1k-αI)TP(A1l-αI)]x(t)+
xT(t)[(A2u-αI)TP(A2v-αI)]x(t)+xT(t)(-2r2P)x(t)≤0.
于是有
xT(t)[(A1k-αI)TP(A1l-αI)-r2P]x(t)≤0,k,l=1, 2, …,N1,k≠l.
(12)
同理, 由(7)可得
xT(t)[(A2u-αI)TP(A2v-αI)-r2P]x(t)≤0,u,v=1, 2, …,N2,u≠v.
现在给出切换律如下:
σ(x,t)∈{p|xT(t)[(Apq-αI)TP(Apq-αI)-r2P]x(t)<
-ε0xT(t)x(t),q=1, 2, …,Np}.
(13)
若σ(x,t)=1,则有下列不等式成立:
xT(t)[(A1i-αI)TP(A1i-αI)-r2P]x(t)<-ε0xT(t)x(t),i=1, 2, …,N1.
(14)
由式(4)得
于是当切换律作用于第一个子系统时,有
xT(t)[(A1-αI)TP(A1-αI)-r2P]x(t)=
(15)
又由不等式(12)和(14)可得
(16)
将(16)代入(15)得

即

(17)
同理,当σ(x,t)=2时,有
(18)

xT(t)[(Aσ-αI)TP(Aσ-αI)-r2P]x(t)<-εxT(t)x(t).
于是
(Aσ-αI)TP(Aσ-αI)-r2P<0.
(19)
根据引理2,由式(19)得
(20)

(21)
于是由不等式(20)和(21)可得
(22)
再由引理2得, 不等式(22)等价于
TAσTPAσ+AσTP+PAσ<0.
(23)
现在考虑Lyapunov函数V(x)=xT(t)Px(t).根据δ算子的定义, 有
xT(t)Pδx(t)+(δx(t))TPx(t)+T(δx(t))TPδx(t)=
再由不等式(23)可得
δV(x)=xT(t)(TAσTPAσ+AσTP+PAσ)x(t)<-εx(t)Tx(t),
即不确定Delta算子切换系统(1)是状态依赖二次D-可稳定的.
3 数值算例
考虑如下Delta算子切换系统(1)的两个子系统:
取N1=N2=2,



下面用这两个特殊的子系统来观察Delta算子切换系统在切换律(13)下的状态轨迹.
A1的极点为-3.333和0.333,A2的极点为-3.078和0.078, 所以子系统S1和S2都不是稳定的.
设置初始条件为x0=[3,2]T, 取ε=0.0001, 取切换律如图1所示.在此切换律下, 系统状态能很快收敛到零, 如图2所示.

图1 切换律

图2 系统的状态轨迹
4 总结
本文考虑了由多面体不确定子系统组成的Delta算子切换系统的二次D-稳定问题.基于Lyapunov稳定性理论, 找到了Delta算子切换系统(1)在任意切换律的作用下是二次D-稳定的的充分条件.最后, 通过数值算例验证了结论的有效性.

