Adaptive Extended Isogeometric Analysis for Steady-State Heat Transfer in Heterogeneous Media

Weihua Fang,Tiantang Yuand Yin Yang

1Nanjing Automation Institute of Water Conservancy and Hydrology,Ministry of Water Resources,Nanjing,210012,China

2Department of Engineering Mechanics,Hohai University,Nanjing,211100,China

3Lake Research Institute,Hydraulic Research Institute of Jiangsu Province,Nanjing,210017,China

ABSTRACT Steady-state heat transfer problems in heterogeneous solid are simulated by developing an adaptive extended isogeometric analysis(XIGA)method based on locally refined non-uniforms rational B-splines(LR NURBS).In the XIGA,the LR NURBS,which have a simple local refinement algorithm and good description ability for complex geometries,are employed to represent the geometry and discretize the field variables;and some special enrichment functions are introduced into the approximation of temperature field,thus the computational mesh is independent of the material interfaces,which are described with the level set method.Similar to the approximation of temperature field,a temperature gradient recovery technique for heterogeneous media is proposed,and based on the Zienkiewicz–Zhu recovery technique a posteriori error estimator is defined to automatically identify the locally refined regions.The convergence and performance properties of the developed method are verified by using three numerical examples.The numerical results show that(1)The convergence speed of the adaptive local refinement is faster than that of the uniform global refinement;(2)The convergence rate of the high-order basis functions is faster than that of the low-order basis functions;and(3)The existing inclusions change the local distributions of the temperature,and the extreme values of the temperature gradients take place around the inclusion interfaces.

KEYWORDS Heterogeneous media;steady-state heat transfer;adaptive XIGA;LR NURBS;heat dissipation

1 Introduction

Heat transfer in heterogeneous media widely exist in many fields.Numerical simulation is an efficient method for solving the common heat transfer problem,and heat transfer problem in heterogeneous media has been investigated with various numerical methods,such as meshless method[1],discrete element method[2],finite element method[3–6]and lattice Boltzmann method[7–9].

Most of the numerical methods used for the heat transfer are based on the finite element method(FEM).However,owing to the requirement of element edges to be lined up with the discontinuity(e.g.,crack,material interface,hole boundary),mesh generation of heterogeneous structure is very time-consuming.In order to overcome the issue,the extended FEM(XFEM)[10]was developed by introducing some special enrichment functions into the FEM approximation,thus the computational mesh is not related to the internal discontinuities.Yu et al.[11]solved steady and unsteady temperature fields in heterogeneous materials using the XFEM.Yvonnet et al.[12]proposed a simple and effective numerical procedure for simulating the Kapitza thermal resistance at an arbitrarily shaped interface using the XFEM combined with the level set method,and high accuracy and robustness can be obtained.Zuo et al.[13]obtained the thermal field in concrete with cooling pipe using the XFEM.Stapór[14]solved nonlinear transient problems with a phase change using the XFEM.The XFEM is a very effective numerical method for modeling the discontinuity,however,it has several drawbacks,for instance,discretization errors exist for complex-shaped structures;onlyC0-continuity of shape function exists;and mesh generation is still required.In order to overcome the above-mentioned shortcomings,the extended isogeometric analysis(XIGA)[15]was introduced by taking the spline functions used in the computer-aided design(CAD)as the shape functions in the XFEM.The XIGA possesses some desirable features besides those in the XFEM,for example,arbitrarily complex structure can be exactly represented,the higher-order continuity of shape functions can be easily obtained,and the traditional mesh generation process is avoided.Due to such excellent characteristics,the XIGA has been applied to solve various discontinuities[16–23].

The adaptive technique can enhance the computational efficiency and the accuracy.Recently,the adaptive XIGA for modeling the discontinuity has received much attention.In order to locally refine,the researchers proposed some splines with local refinement ability,such as T-splines[24,25],Hierarchical B-splines[26],PHT-splines[27],Hierarchical NURBS[28],and LR B-splines[29,30].Nguyen-Thanh et al.[31,32]presented an isogeometric analysis based on PHTsplines which facilitates adaptive refinement,and solved two-dimensional solids and thin shell.Later,they presented a multi-patch isogeometric large deformation thin shell formulation based on RTH splines,and developed a stress recovery technique to drive the adaptive h-refinement procedure[33].Recently,we proposed the adaptive LR B-splines based XIGA and successfully simulated inclusions[34],holes[35],and cracks[36–38].Yang et al.[39]developed an adaptive XIGA based on the PHT-splines for cracked thin plates and shells.

The existing studies reveal the efficiency of the adaptive XIGA in modeling discontinuous problems.Studies on modeling heat transfer problems in heterogeneous media using an adaptive XIGA have not be found in literature.The purpose of this study is to solve the steady-state heat transfer problems in heterogeneous media using an adaptive XIGA.We modeled the steadystate heat transfer problems using an adaptive LR B-splines based IGA[40],so this work is an extension of our previous work[40].The methods based on LR B-splines possess the adaptable and diversified local refinement scheme,however,the LR B-splines can not exactly represent some complex geometries.LR NURBS[41]by combining NURBS with the LR B-spline theory can effectively overcome this issue.Hence,the adaptive LR NURBS based XIGA is adopted in this work.The LR NURBS basis functions are utilized for the structure discretization and the approximation of field variables.The smoothed temperature gradient field[42]is constructed,and according to the Zienkiewicz–Zhu recovery technique[43],a posteriori error estimator is evaluated to guide the local refinement.The main advantages of the proposed method include:(a)The geometry can be exactly described,i.e.,without the discretization error;(b)The computational mesh is not related to the material interfaces,so mesh generation for heterogeneous media is very simple,and good shape elements can be obtained;(c)Only the required regions are automatically and locally refined;(d)The accuracy and the computational cost can be concurrently taken into account;and(e)Fast convergence rate is achieved.

The organization of this article is as follows:The main equations for steady-state heat transfer in heterogeneous media are described in Section 2;Section 3 presents the adaptive LR NURBS based XIGA for steady-state heat transfer in heterogeneous media;Section 4 demonstrates the accuracy and the effectiveness of the proposed method;and some main concluding remarks are given in Section 5.

2 Problem Description

An isotropic heterogeneous media is considered.According to the theory of heat transfer,the temperatureTin isotropic solid satisfies the following differential equations and boundary conditions:

with

wherek,k1andk2denote the thermal conductivity parameter;qvis the heat source;andqnare the prescribed temperature and heat flux density on the boundary,respectively;Twis the ambient temperature,whilehis the convective heat transfer coefficient;T1andT2are the temperatures of two materials on the interface;ndenotes the outward normal on the boundary.

The first and the second class boundary conditions(Eqs.(2a)and(2b))mean that the temperature function and the heat flux density on the boundary of the object are known,respectively.The third class boundary condition(Eq.(2c))refers to the convective or radiative heat transfer on the boundary of the object.Assumed the perfect contact between two different solids,continuous temperature and heat flux exist on the interface,which is known as the fourth class boundary condition(Eq.(2d)).

Based on the variational principle,the steady-state heat transfer problem in heterogeneous media may be changed into solving the extreme-value problem of the following function:

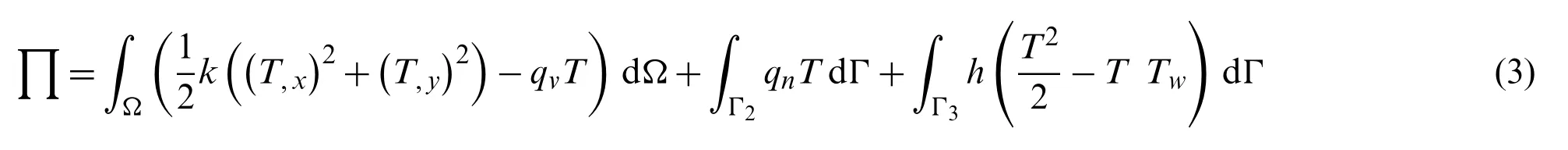
3 Adaptive LR NURBS Based XIGA for Heat Transfer Problem

3.1 XIGA for Steady-State Heat Transfer in Heterogeneous Media

From Eq.(2),we can find that the temperature is continuous across the material interface,but the temperature gradients are discontinuous.According to the XFEM theory,the XIGA approximation for the temperature field can be written as[11]

with

whereRiandRjdenote the LR NURBS basis functions[41],which are defined with the local coordinates(ξ,η)in the parametric domain;Tiandajare the temperature and the enrichment variable at control pointiandj,respectively;I1andI2are the set of control points in the discretized domain and the set of control points whose supports are intersected by the material interface,respectively;ψis the enrichment function,andφidenotes the level set function value at theith control point.

Combining Eq.(3)with Eq.(4)and applying variation rule lead to

whereTis the global temperature vector.KandFare the global heat transfer matrix and temperature load vector,respectively.In addition,the element contributions toKandFare written as

where

with

For elements without any enriched control point,the numerical integration is conducted with(p+1)×(q+1)integral points,wherepandqare the order of LR NURBS basis function in theξandηdirections,respectively.For elements containing the material interface,the sub-triangle scheme[36]is used,and seven integration points are applied in each sub-triangle element.

Taking into account the first class boundary condition(Eq.(2a)),the temperatures and enrichment variables of control points are solved with Eq.(6).It is noted that the temperature approximation presented in Eq.(4)can directly satisfy the fourth class boundary condition[11],thus the fourth class boundary condition in this method does not need special treatment.

3.2 Error Estimation

According to the Zienkiewicz and Zhu method[43],we can use the smoothed temperature gradients instead of the exact value to conduct the error estimation.The temperature gradients across the material interface are discontinuous,similar to the temperature approximation,the approximation of the smoothed temperature gradients can be expressed as

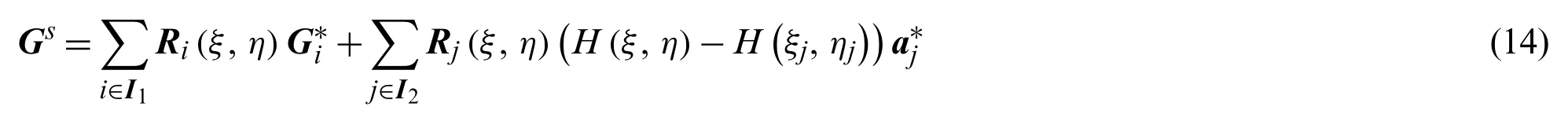
with

whereHequals 1 on one side of a material interface and −1 on the other side,andare the smoothed temperature gradient vector and the corresponding enrichment variable vector at the control pointi,respectively.

Eq.(14)is rewritten in a matrix form,i.e.,

Through a least square fit between the temperature gradientsGhobtained from the XIGA and the smoothed temperature gradientsGs,the following equation can be obtained

Minimizing Eq.(17)about the unknown variable vectorg∗yields

where

The previous studies[40,44]show that the error in heat dissipation can effectively evaluate the accuracy of the numerical method for the heat transfer problems.According to the Zienkiewicz and Zhu error estimation[43],the posteriori error estimator is calculated with the smoothed temperature gradients instead of the exact value.For one element with areaΩe,theL2error norm in the heat dissipation and the heat dissipation norm of the smoothed temperature gradient field are given by

The relative error for each element is evaluated with the following equation:

4 Numerical Results

Three numerical examples are analyzed to demonstrate the accuracy and the effectiveness of the present method.The first example,whose exact solution is available,is used to test the accuracy of the method.The second example considers a plate with one circular inclusion.The third example simulates a plate with four circular inclusions.The quadratic-order LR NURBS basis functions are used if not special specified in the following examples.

4.1 A Bi-Material Ring

Consider a bi-material ring with fixed temperatures on the inner and outer surfaces,as shown in Fig.1a.r1=2m,r2=4.2m,r3=6m,T1=0◦C,andT3=20◦C.The materials of the inner and outer rings are ordinary concrete and foamed concrete,and the thermal conductivity coefficients of the ordinary concrete and the foamed concrete are 10 KJ/(mh◦C)and 0.377 KJ/(mh◦C),respectively.Due to the symmetry,a quarter of the bi-material ring is taken into account for the analysis,and the adiabatic boundary condition is imposed on the symmetry faces,as shown in Fig.1b.

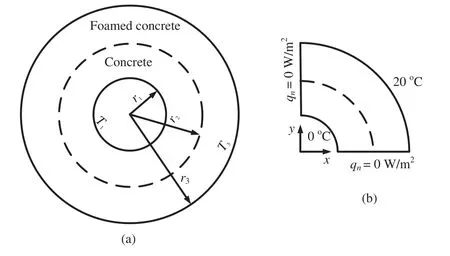
Figure 1:Problem definition for a bi-material ring

The exact temperatures in the bi-material ring are expressed as[45]:

in whichris the radius.

Fig.2 shows the uniform mesh and the corresponding control points labeled with circles for the original analysis.The orders of LR NURBS basis functions along the circumferential and radial directions are 2 and 1,respectively.It is noted that the computational mesh is independent of the material interface labeled in red line.

Figure 2:Original computational mesh and control points

Fig.3 shows the four subsequent meshes in terms of the adaptive procedure.The local refinement first occurs around the material interface,then near the outer surface of the ring,finally around the inner surface of the ring and the material interface.These refined regions are as expected.

Figs.4–6 show the distribution contours of the temperature and the temperature gradients obtained from the present method and the exact solution after four refinement steps,and the absolute errors are also plotted.From Figs.4–6,it is found that the adaptive XIGA offers highly accurate results.

The temperatures along the radial direction are plotted in Fig.7.The results obtained by the adaptive XIGA match well with the exact solution,which again verifies the excellent accuracy of the proposed method.

Fig.8 presents the convergence curves of theL2error norm in the heat dissipation for both refinement schemes.It is obvious that the convergence speed of the adaptive local refinement(ALR)is faster than that of the uniform global refinement(UGR),and the same conclusion was obtain in the steady-state heat transfer problems in homogeneous media[40].

Figure 3:Locally refined meshes based on the error estimator at the Step 1(a),Step 2(b),Step 3(c)and Step 4(d)

Figure 4:Temperature contours for the adaptive XIGA solution(a),the exact solution(b)and the absolute error(c)

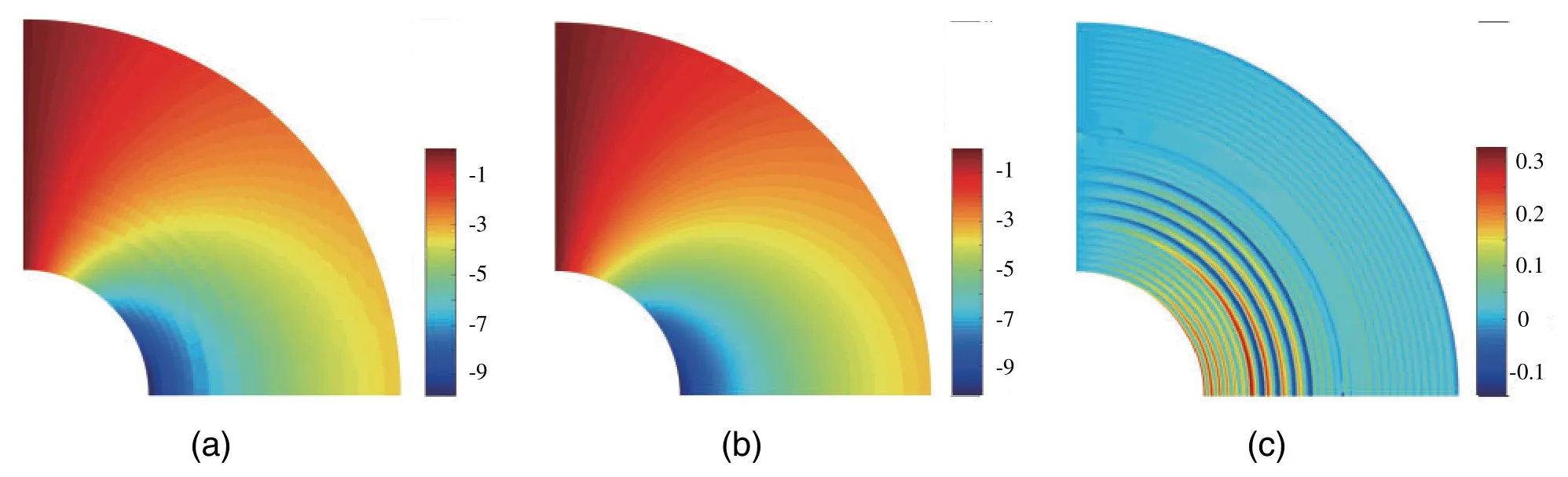
Figure 5:Temperature gradient contours in x-direction for the adaptive XIGA solution(a),the exact solution(b)and the absolute error(c)

Figure 6:Temperature gradient contours in y-direction for the adaptive XIGA solution(a),the exact solution(b)and the absolute error(c)

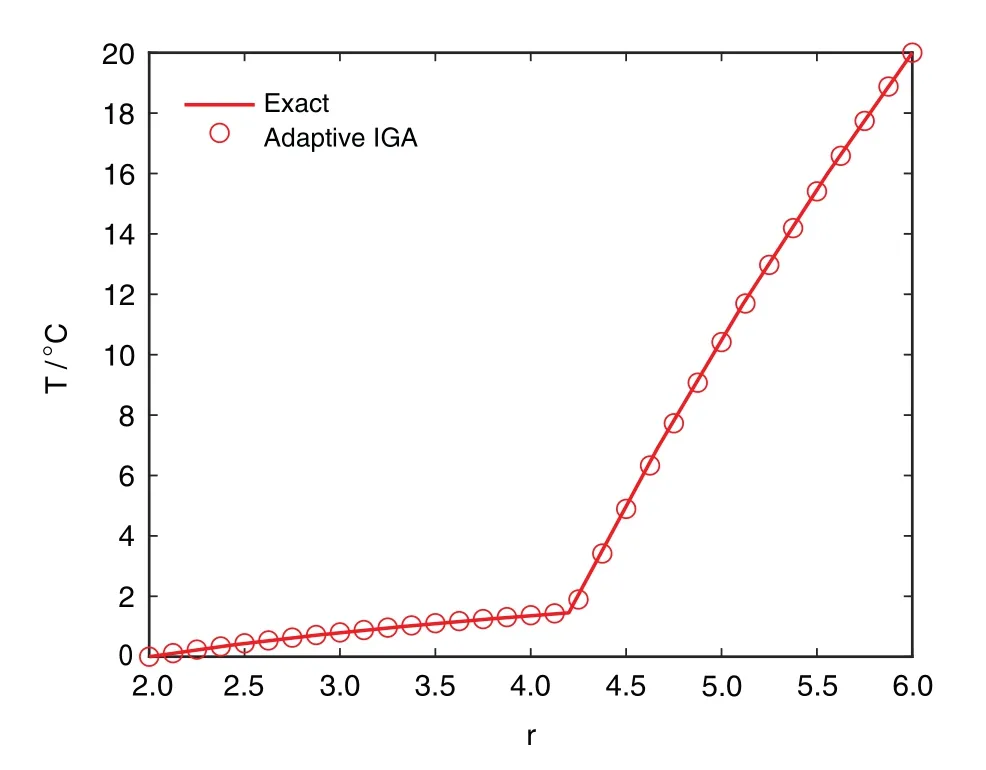
Figure 7:Temperatures along the radial direction

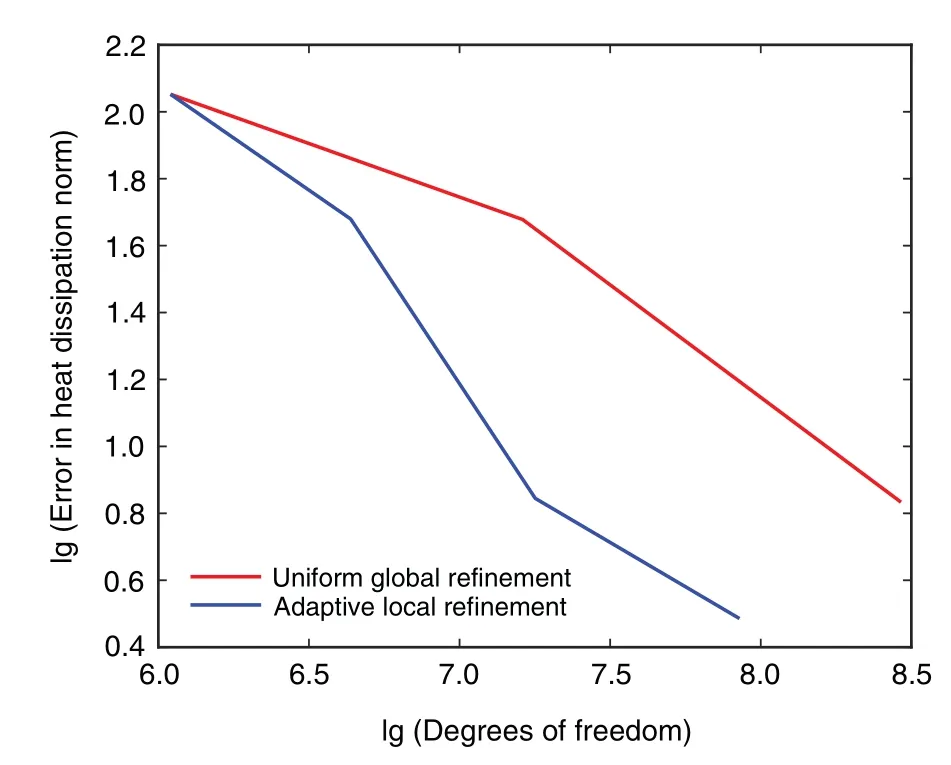
Figure 8:Comparison of convergence results between the ALR and the UGR

4.2 A Square Plate with One Circular Inclusion

The second example considers a square plate with one circular inclusion with a radius of 2 m,as shown in Fig.9.The upper and lower surfaces are assumed to be adiabatic.Prescribed temperature on the left boundary is 400◦C.The ambient temperature on the right side is 85◦C,and the convective heat transfer coefficient equals 160 W/(m2·◦C).The thermal conductivity coefficients of materials B and A are 100 W/(m·◦C)and 200 W/(m·◦C),respectively.

Figure 9:Problem definition for a square plate with one circular inclusion

Fig.10 presents the initial mesh and the corresponding control points.

Figure 10:Original computational mesh and control points

Fig.11 shows the three subsequent meshes in terms of the adaptive procedure.From Fig.11,it is found that the local refinement takes place around the material interface,and the refined zone gradually approaches to the material interface with increasing the number of refinements.This shows that big error exits around the inclusion interface,as expected.

Figure 11:Locally refined meshes based on the error estimator at the Step 1(a),Step 2(b)and Step 3(c)

The distribution contours of the temperature and the temperature gradients inxandydirections after three refinement steps are shown in Figs.12 and 13.The existing inclusion changes the local distribution of the temperature,and the extreme values of the temperature gradients take place around the inclusion interface.

Figure 12:Temperature contours

Figure 13:Temperature gradient contours in x-direction(a)and in y-direction(b)

Fig.14 shows the variation of the relative error in heat dissipation norm with increasing the degrees of freedom(i.e.,increasing the refinement step number)obtained with the adaptive XIGA with different basis orders.Forp=q=1,the present method becomes the standard extended finite element method.It is found that the convergence rate of the quadratic basis function is faster than that of the linear basis function with increasing the refinement step number.

4.3 A Square Plate with Four Circular Inclusions

In order to demonstrate the effectiveness of the present method for simulating the steady-state heat transfer in complex heterogeneous media,a square plate with four identical circular inclusions with a radius of 1.2m is taken into account,as shown in Fig.15.The upper and lower boundaries are assumed to be adiabatic,and the prescribed temperatures on the left and right boundaries are 400◦C and 100◦C,respectively.In addition,the thermal conductivity coefficient of matrix is 100 KJ/(mh◦C),while the thermal conductivity coefficient of inclusions is 1000 KJ/(mh◦C).

Figure 14:The variation of the relative error with the refinement step number

Figure 15:Problem definition for a square plate with four circular inclusions

The computation is first conducted on the uniform starting mesh,as shown in Fig.16.The three subsequent meshes in Fig.17 are generated according to the adaptive procedure.The refined regions are the same as those in the previous example,i.e.,the local refinement takes place around the material interface,and the refined zone gradually approaches to the material interface with increasing the refinement steps.

Figure 16:Original computational mesh and control points

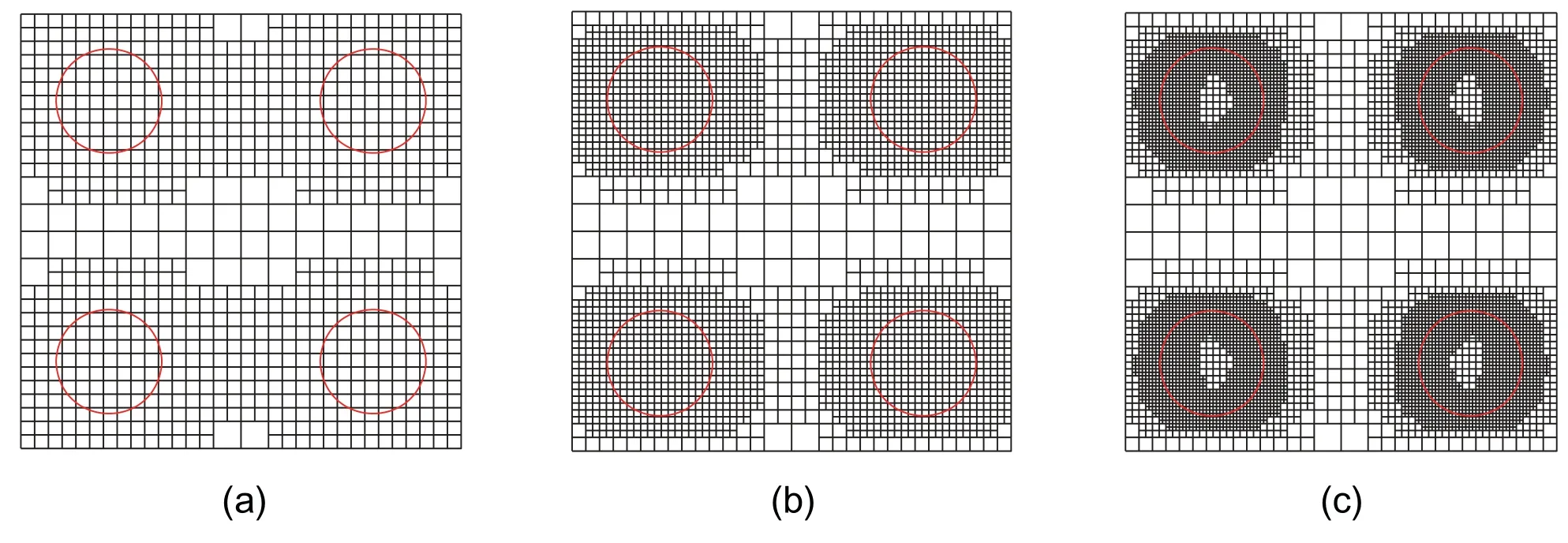
Figure 17:Locally refined meshes based on the error estimator at the Step 1(a),Step 2(b)and Step 3(c)

In addition,we plot the temperature contours in Fig.18 and the temperature gradient contours in Fig.19 on the final mesh.From Figs.18 and 19,it is found that the existing inclusions change the local distributions of the temperature,the extreme values of the temperature gradients take place around the inclusion interfaces,and the distributions of the temperature gradients are almost the same around each inclusion.

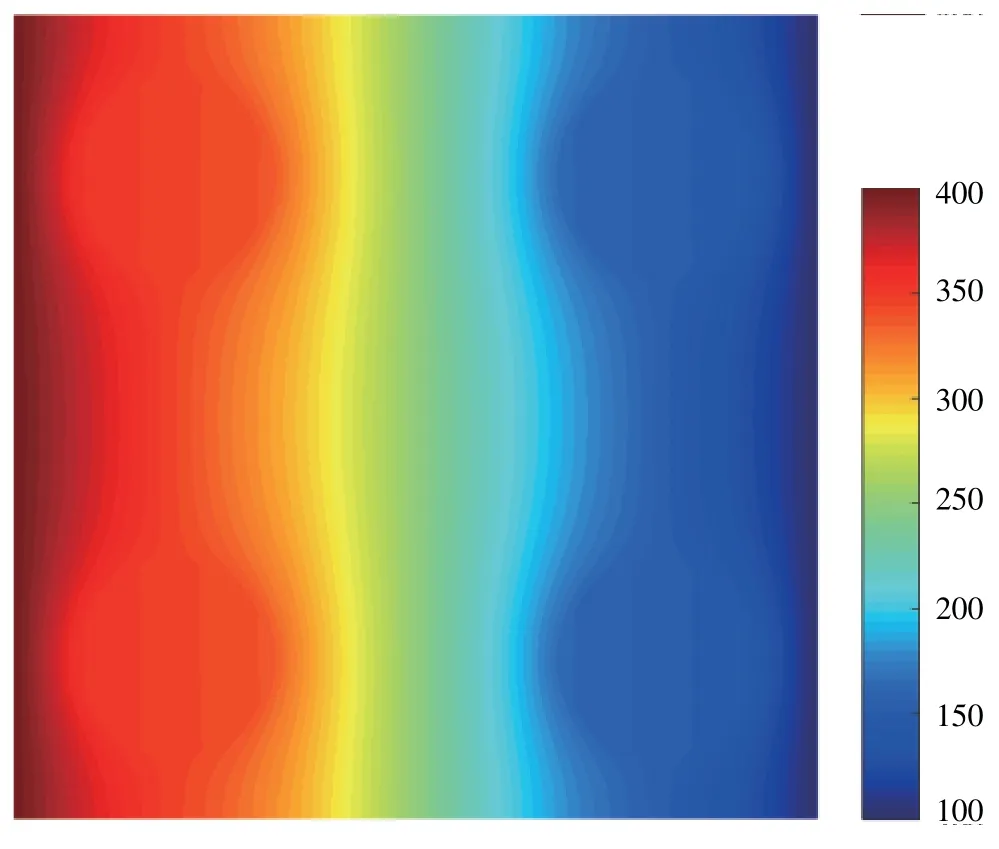
Figure 18:Temperature contours

Figure 19:Temperature gradient contours in x-direction(a)and in y-direction(b)

5 Conclusions

An adaptive LR NURBS based XIGA for steady-state heat transfer problems in heterogeneous media is proposed.Because of the adaptable and diversified local refinement scheme and the exact description of complex geometry,the LR NURBS are adopted in the XIGA.The mesh is not related to the material interfaces by introducing special enrichment functions into the approximation of temperature field.A temperature gradient recovery technique for heterogeneous media is proposed,and the local refinement is automatically conducted based on the error estimator,which is constructed with the recovered temperature gradient field.Numerical results verify the excellent performance of the developed method.

The present approach owns some desirable features and its further developments include unsteady-state heat transfer and thermoelastic problems in heterogeneous media.In addition,the computation cost of the present method will be compared with that of conventional method by solving the large scale heterogeneous media.

Acknowledgement:The authors wish to express their appreciation to the reviewers for their helpful suggestions which greatly improved the presentation of this paper.

Funding Statement:The authors received no specific funding for this study.

Conflicts of Interest:The authors declare that they have no conflicts of interest to report regarding the present study.