分数阶随机时滞微分方程解的存在唯一性

王苗苗，丁小丽，李佳敏

(西安工程大学 理学院，陕西 西安 710048)

0 引 言

分数阶微积分在流体力学[1]、控制论学[2]和生态学[3]等学科领域中有较为普遍的应用,国内外学者对相关问题进行了大量的研究。在许多实际应用中,干扰因素或不确定因素是不可避免的,例如人口的出生与死亡,如果不考虑随机因素的干扰,就有可能出现人口剧增的现象，不符合实际情况。在随机事件中,可以根据大量的试验数据确定某个随机变量,并附加初始条件建立随机微分方程的数学模型,从而推断出整体的发展变化规律。因此,人们将随机现象与分数阶微分方程结合进行研究。文献[4]建立了多时间尺度分数阶随机微分系统的数学模型,利用Picard逐步逼近法证明了该系统解的存在唯一性,同时求解了It-Doob型线性和非线性多时间尺度分数阶随机微分方程的闭式解；SAKTHIVEL等利用不动点定理，研究了一类带有脉冲的分数阶随机微分方程温和解的存在性[5]；BENCHAABANE等运用半群理论和Picard型近似序列,得到了一类非线性Sobolev型分数阶随机微分方程存在唯一温和解的充分条件[6]；DOAN等利用一个时间加权范数,在Caputo意义下考虑了分数阶随机微分方程解的整体存在性和唯一性,其中分数阶系数满足全局Lipschitz条件[7]。

随着研究的深入,人们发现，对于一些相对复杂的现象时,可能有滞后现象的出现,应考虑未来的状态不仅依赖于现在的状态,还依赖于先前的历史状态。文献[8-9]表明用分数阶时滞微分方程比一般的微分方程来刻画更符合实际,使得问题的描述更加真实准确；YAN等给出了HIV病毒传播的分数阶时滞微分模型，并讨论了该模型的稳定性[10]；CUI等研究了Hilbert空间中一类具有无限时滞的分数阶随机微分方程温和解的存在性[11]；SAKTHIVEL等利用随机分析理论和不动点定理,研究了一类分数阶随机微分方程线性和半线性情形的均方伪几乎自守弱解的存在唯一性[12]；杜思嘉运用Banach不动点定理以及在特定条件下区间值分数阶时滞微分方程的关系,证得区间值Caputo一阶分数阶时滞微分方程解的存在性和唯一性[13]。ZHAGN等研究了一类有限时滞的分数阶随机微分方程,利用Picard迭代法和广义Gronwall不等式,给出了分数阶随机微分方程解存在唯一的充分条件；在同一思路下,讨论了分数阶q>1的有限时滞随机微分方程解的存在性和唯一性[14]。吴艾卿等通过使用Lyapunov稳定性分析方法,研究了一类具有高度非线性系数的中立型混杂随机微分方程解的存在唯一性[15]。在以上研究的基础上,LU等利用Banach收缩原理,给出了变时滞非线性Caputo分数阶中立型随机微分方程平凡解均方渐近稳定的一个充分条件,而且不要求时滞的有界性[16]。此外,文献[17-18]给出了脉冲分数阶随机微分方程解的存在性结果。这些研究成果为研究分数阶随机时滞微分方程解的适定性提供了理论基础。

微分方程解的存在唯一性是研究微分方程解的适定性的一个关键问题。由于缺乏求解分数阶和随机微积分控制的非线性动力系统的通用技术,在采用离散化方法获得近似解之前,研究解的存在唯一性是前提与基础。常用研究方法有Picard逐步逼近法和运用Banach不动点定理,其中Picard逐步逼近法是较为重要的近似计算方法。文献[4]和[19]均是利用Picard逐步逼近法,研究了不同类型的分数阶随机微分方程初值问题解的存在唯一性。可见,关于分数阶随机微分方程和分数阶时滞微分方程解的存在唯一性已经有了一些研究成果,但关于分数阶随机时滞微分方程解的研究结果较为少见。本文将分数阶随机微分方程和时滞微分方程的理论结合并延伸,将Picard逐步逼近法推广到分数阶随机时滞微分方程,并运用积分算子理论,研究分数阶随机时滞微分方程解的存在唯一性问题,分析该方程解对初值的连续依赖性。

1 分数阶积分及相关引理

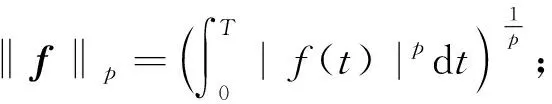
定义1[4]设0<α<1,∀t∈Ω,函数f(t)∈L1(Ω;Rn)的α阶Riemann-Liouville型分数阶积分定义为

其中Γ(·)是Gamma函数,

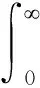
定义2[4]设0<α≤1,f(t)∈L1(Ω;Rn),f(t)关于(dt)α的积分定义为

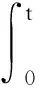
引理1[20]设0<α<1,a(t)是在时间区间Ω上的一个局部可积的非负函数,b(t)和g(t)是在Ω上的非负非减且有界的连续函数。如果v(t)非负,在Ω上局部可积,且满足

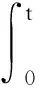
则

推论1[20]假设满足引理1中的条件,且a(t)在Ω上非减,则

其中Eα为Mittag-Leffler函数,

2 解的存在性与唯一性

考虑如下形式的分数阶随机时滞微分方程

(1)

式中：x(t)=ξ={ξ(θ):-τ≤θ≤0};τ>0，为给定的时滞量；b,σ2∈C(Rn×Rn×[t0,T];Rn),σ1∈C(Rn×Rn×[t0,T];Rn×m),是Borel可测函数；B(t)=(B1(t),B2(t),…,Bm(t))T是在完备概率空间{Ω,F,P}上的m维布朗运动;ξ∈C([-τ,0];Rn),且E|ξ(θ)|2<∞。

为了证明方程(1)解的存在性,定义2个算子J1、J2,分别为

式中：0<α≤1;φ(t)∈C(Ω;Rn)。

引理3 设0<α≤1,φ(t)∈C(Ω;Rn),则

(J1J2φ)(t)=(J2J1φ)(t)

证明由算子J1、J2的定义,可得

引理4 设0<α≤1,φ(t)∈C(Ω;Rn),i=1,2,3,…,有下列关系成立:

(2)

(3)

证明当i=1时,显然

设式(3)∀i∈N+成立,验证式(3)对i+1也成立。根据归纳假设可以得到

使用变量代换s=δ+ω(t-δ),有

式中：B(·,·)是Beta函数,

基于以上的结果,得到

因此∀i∈N+,

特别地,当α=1时,

即式(2)成立。

1) Lipschitz条件:

2) 线性增长条件:

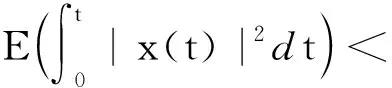
证明1) 设x(0)(t)=ξ(0),根据定义2,方程(1)可变形为

2) 对于k=0,1,2,…,构造Picard迭代序列{x(k)(t)},即

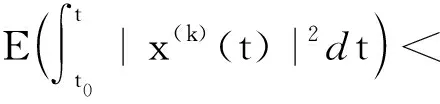
由于ξ(0)∈M2([t0-τ,T];Rn),x(k)(t)∈M2([t0-τ,T];Rn),因此x(k+1)(t)∈M2([t0-τ,T];Rn),即x(k)(t)∈M2([t0-τ,T];Rn)。

3) 证明Picard迭代序列{x(k)(t)}在区间[t0,T]上均方一致收敛。

利用(a+b+c)2≤3(a2+b2+c2)及Hölder不等式、It积分的等距性、Lipschitz条件,有

E|x(k+1)(t)-x(k)(t)|2≤

|σ2(x(k)(s),x(k)(s-τ),s)-

E|x(k)(s)-x(k-1)(s)|2ds

(4)

为了方便起见,定义

e(k+1)(t)=E|x(k+1)(t)-x(k)(t)|2

根据算子J1、J2的定义,式(4)可以表示为

e(k+1)(t)≤((A1J1+A2J2)e(k))(t)

由文献[21]中的性质2.2,可以得到,J1与J2对φ(t)∈C(Ω;Rn)是非递减的。对k进行数学归纳,则

e(k+1)(t)≤((A1J1+A2J2)ke(1))(t)

(5)

当k=1时,

e(2)(t)≤((A1J1+A2J2)e(1))(t)

结果显然成立。假设式(5)∀k(k=1,2, 3,…)成立,验证式(5)对k+1也成立。根据归纳假设,可以得到

因此e(k+1)(t)≤((A1J1+A2J2)ke(1))(t)成立。

由文献[21]中的性质2.1可以得到,J1和J2是C(Ω;Rn)上的紧算子; 由引理3知,J1和J2可交换,又σ(J1)=σ(J2)={0},其中σ(·)表示算子的谱。因此,{x(k)(t)}是Cauchy序列,所以序列{x(k)(t)}在区间[t0,T]上均方一致收敛。

4) 证明序列{x(k)(t)}的极限是原方程的解。

5) 证明方程(1)解的唯一性。

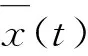
根据引理1,得到

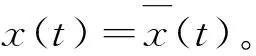
3 解对初值的连续依赖性

讨论当初值条件发生微小变化时,对方程的解造成怎样的影响。为此,设存在一个充分小的正数ε,使得|ξ-η|<ε。给出下列方程

(6)

式中：z(t)=η={η(θ):-τ≤θ≤0}。这里假设方程(6)已经满足解的存在唯一性条件。

定理2 设z(t)是方程(6)的解,那么∀t∈[t0,T],有

其中Eα为Mittag-Leffler函数,

证明根据方程(1)和方程(6)的解

由引理1和推论1,可得

由此不难发现,当初值条件有一个微小的变化时,解也有一个相应的微小变化,即解对初值具有连续的依赖性。定理2得证。

4 结 语

研究了带有时滞变量的分数阶随机微分方程解的存在唯一性和解对初值的连续依赖性。利用Picard逐步逼近法的思想并结合积分算子理论,减小了传统迭代方法的计算复杂度。给出了分数阶随机时滞微分方程所满足的Lipschitz条件和线性增长条件,在此条件下证明了方程存在唯一解。通过使初值条件发生微小的变化，研究了解的连续依赖性。然而，对于文中这类分数阶随机时滞微分方程,即使满足了解的存在唯一性定理,也很难找到其解析解，需要求解它的数值解。关于其数值解法有待进一步研究。