谐波齿轮传动机构不同参数柔轮的装配应力分析*
张育玮,姚廷强,杨 斌
(昆明理工大学 机电工程学院,云南 昆明 650504)
0 引 言
工业机器人的研究与发展是评价国家工业科技创新能力的一个标志。而谐波减速器作为工业机器人中的重要功能部件,其特点为:高减速比、轻量化、高定位精度、高传动效率等。目前,在我国对工业机器人的研究中,其中的谐波减速器方面还存在着技术瓶颈。因此,国内许多科研人员一直致力于谐波齿轮传动技术的研究。
在谐波齿轮传动技术的研究中,对柔轮的变形及应力分布的探索通常是研究中的重点。我国的学者沈允文[1]对柔轮的位移及变形做了大量的研究,他在研究中采用光滑圆柱壳体对柔轮进行了应力分析。同时,为了减少计算成本,学者们对此采用了一些简化。阳培等人[2]将齿圈等效成当量圆环,建立了柔轮四分之一有限元模型,得到了柔轮在波发生器作用下的变形及应力分布情况。余飞鹏等[3]采用有限元软件,分别对不同负载状态下柔轮壁厚对其应力及变形的影响情况进行了仿真分析,得到了柔轮壁厚对其力学性能的影响规律。张立勇等[4]采用有限元的方法,得到了谐波传动径向变形量对啮合特性的影响规律,为合理选择变形量得到更好的啮合性能提供了参考。邹创[5]通过实验计算出了啮合的边界条件,分析结果表明,柔轮变形及应力分布主要受波发生器的作用影响。李志刚[6]通过对柔轮热与结构耦合的有限元分析,得到了柔轮的最佳工作条件。杨建[7]考虑了不同轴承的作用下柔轮的应力分布。邢静忠等[8]分别计算了不同工况下柔轮最高应力分布规律,及不同参数对柔轮不同工况负载应力的影响规律。董慧敏等[9,10]研究了不同参数对柔轮应力的影响,从而实现了对柔轮的优化设计。李志刚[11]以柔轮体积为目标函数,对柔轮几何参数进行了优化设计。
谐波齿轮失效原因主要在于柔轮齿应力过高,以及柔轮结构参数引起的应力和应变等,因此,对柔轮的应力分布规律的研究是十分重要的课题。
本文基于ANSYS有限元软件,分析不同设计结构参数对柔轮内部各部分应力变化规律,为柔轮的参数设计及优化提供参考。
1 有限元建模及求解
1.1 谐波减速器的几何模型
本文以某杯型谐波减速器为研究对象,建模时以控制变量的方法,根据柔轮的结构特性以不同齿形、柔轮的长径比、齿圈宽度、筒体厚度、筒体与法兰的过渡圆弧建立柔轮模型。
其几何模型如图1所示。

图1 渐开线谐波减速器的柔轮结构示意图da2—齿顶圆直径;dn2—柔轮内壁直径;df2—柔轮外壁直径;B—齿圈宽度;R4—筒体与杯底过渡圆角半径;C1—柔轮筒壁厚度;C2—凸缘厚度;dt—杯底凸缘直径;d—杯底圆孔直径
其几何参数如表1所示。

表1 渐开线谐波减速器结构参数表
其中,柔轮材料为55Si2Mn,弹性模量E=197 GPa,泊松比μ=0.254 8;减速器为凸轮式波发生器,宽度为B1=15 mm,长轴直径为a=97.75 mm,短轴直径为b=96.75 mm。
笔者通过UG构建柔轮与波发生器三维数字化装配模型,并转化成Parasolid,逐一导入ANSYS19.0有限元仿真平台;装配时,采用绝对坐标系定位,在三维软件中不需要其他的装配约束。
柔轮的有限元模型如图2所示。

图2 柔轮有限元网格模型
1.2 网格划分
由于柔轮的齿数量较多,且柔轮筒体属于薄壁构件,变形量相对柔轮壁厚而言属于大挠度的非线性变形,高质量的网格会大幅度提高结果的准确性。考虑网格的合理性及连续性,根据柔轮结构特点及从划分合理规则的网格出发,在网格划分前,笔者先对柔轮进行体分割。
柔轮切分示意图如图3所示。

图3 柔轮切分示意图Ⅰ—齿圈前沿;Ⅱ—齿圈;Ⅲ—筒体;Ⅳ—筒体与法兰过渡圆弧;Ⅴ—法兰凸缘
此处,体分割的目的就是将柔轮分割成可以用sweep方式进行规则的六面体网格划分。
1.3 边界条件的定义
在未装配前,柔轮的原始剖面呈圆形,波发生器的最大直径比柔轮内圆直径略大;把波发生器装入柔轮内时,迫使柔轮发生变形。
为了更好地贴近实际的工况,本研究把波发生器外柱面定义为理想刚性目标面,将柔轮的内柱面定义成柔性接触面;接触类型采用的是“刚—柔”面面接触,根据谐波减速器实际装配情况施加边界条件,并将柔轮底部法兰面上的所有节点上的位移进行全约束。
2 空载下柔轮接触分析
2.1 柔轮的变形分布规律
理论上,波发生器装入柔轮中时,柔轮在预应力作用下会被挤压成椭圆形状,柔轮长轴被挤压变长,柔轮在短轴方向被拉伸向圆心收缩。
筒体外壁沿轴向方向的变形曲线如图4所示。

图4 筒体外壁沿轴向的变形曲线
由图4可以看出:从柔轮的杯口到杯底,柔轮的变形量逐渐减小;柔轮波发生器长轴方向的变形量大于同一位置其他方向上的变形量;最大变形量位于杯口长轴处,最大变形量为0.796 34 mm。
笔者对柔轮齿圈的截面1(即Z=0)和截面2(即Z=15)进行仿真分析,其结果如图5所示。

图5 筒体外壁各截面变形量
由图5可知:在波发生器的作用下,柔轮的齿圈截面变形呈上下左右对称,最大等效变形量在波发生器长轴处,等效变形量最小均处在与长轴夹角45°处;因为柔轮齿圈的等效变形量从波发生器的短轴,沿着周向方向一直到波发生器的长轴,遵循先降低后增大规律;波发生器工作一周,柔轮上的变形量要从小到大变化4次;其中截面1的变形量最大,截面2的变形量最小。
2.2 柔轮的应力分布规律
柔轮筒体外壁轴向应力分布情况如图6所示。

图6 筒体外壁轴向应力分布曲线
波发生器装配后,谐波减速器筒体长轴处等效应力大于短轴处等效应力;筒体上的等效应力在整体上先增大后减小,最后又增加少许。这种等效应力变化的原因是波发生器柔轮受到波发生器集中载荷和过渡圆角的影响;在齿圈位置变化幅度较大,而在筒体位置变化幅度较小,说明谐波减速器装配后,齿圈位置为危险截面,沿波发生器长轴方向筒体齿圈位置最大应力达到192 MPa。
柔轮齿圈截面周向应力分布情况如图7所示。
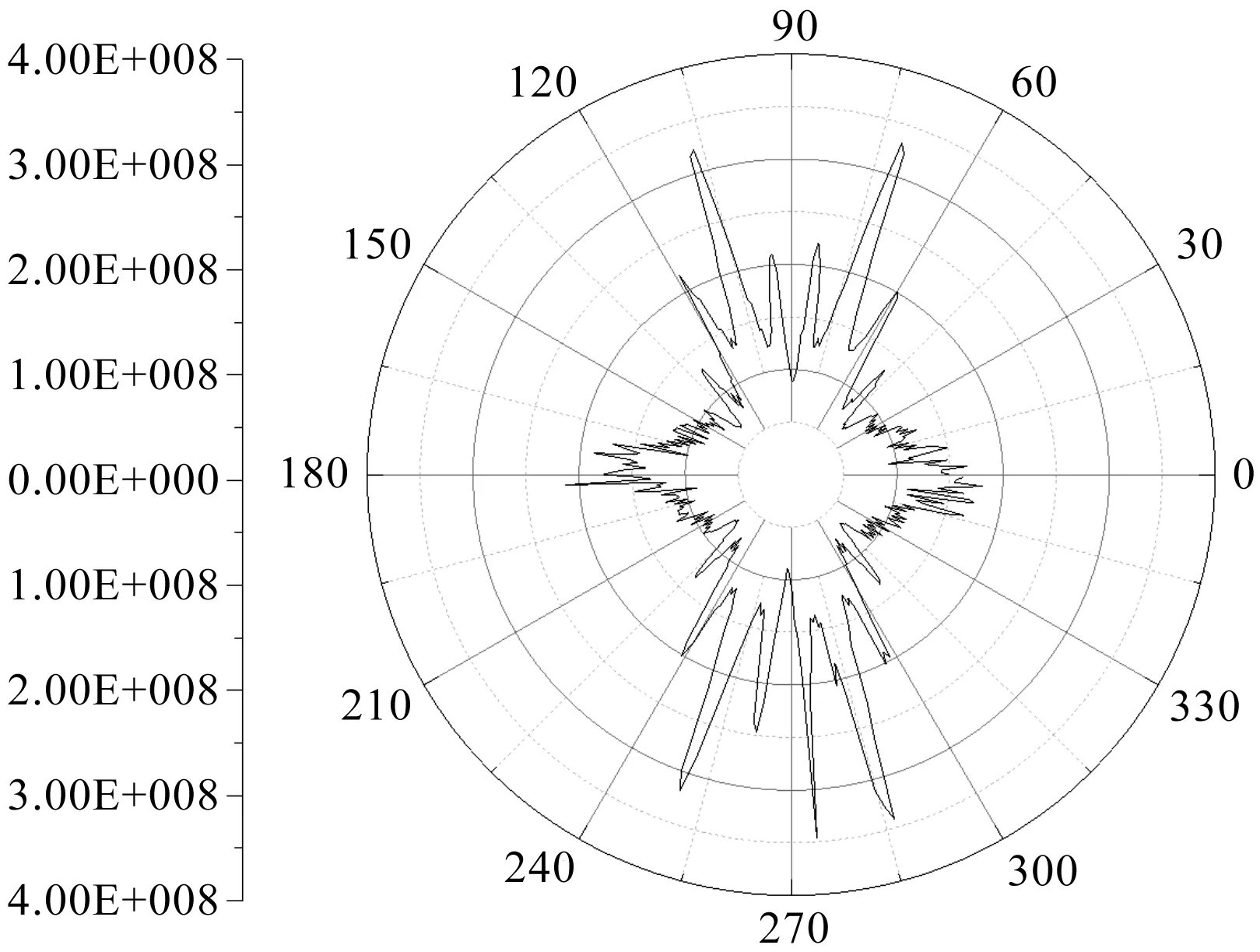
图7 齿圈截面周向应力分布曲线
由图7可以看出:无论是波发生器长轴处还是波发生器短轴处,柔轮的齿圈截面周向应力分布波动比较明显;齿圈截面长轴处应力波动比短轴处更加剧烈,幅值也更大;等效应力最大值达到了300 MPa。
3 不同负载下柔轮的应力分析
在有限元模型参数不变的情况下,笔者利用有限元技术,通过改变其负载的大小,对柔轮进行仿真分析。
柔轮在节圆位置处与刚轮发生啮合,为了模拟扭矩,笔者在柔轮长轴的轮齿节圆处施加切向力,并提取此处齿宽方向上的两排节点,在节点上施加集中力与轮齿节圆相切,其中,切向力、节点数量和节圆半径的乘积为扭矩大小。
笔者分别取负载为0 N·m、40 N·m、80 N·m进行仿真分析。
其中,0 N·m时柔轮应力的分布情况如图8所示。
由图8可以看出,在空载时,柔轮应力分布关于X、Y轴对称。
当负载为40 N·m时,柔轮的应力分布情况如图9所示。
当负载为80 N·m时,柔轮的应力分布情况如图10所示。

图8 0 N·m时柔轮应力云图

图9 40 N·m时柔轮应力云图

图10 80 N·m时柔轮应力云图
由图(9,10)可以看出:在负载为40 N·m、80 N·m时,扭矩方向上柔轮最大应力发生偏移。这是因为柔轮的应力主要集中在齿圈位置处,筒体应力比齿圈应力小,当轮齿沿着扭矩方向啮合时受载更大;同时可以发现,负载越大,柔轮的整体应力也越大。
4 空载下不同参数柔轮的应力分析
4.1 长径比对柔轮应力分布的影响
柔轮长径比是柔轮设计的重要参数,其值的大小将直接影响柔轮结构紧凑性,从而影响谐波减速器轻量化设计要求;同时,对柔轮应力影响也不可忽视。
此处笔者取柔轮长径比在0.5~1范围内的柔轮,在保持其他参数不变的前提下,分析6组不同数值下柔轮的应力变化规律,其结果如图11所示。

图11 长径比对柔轮应力影响
从图11中可以看出:随着柔轮长径比的增大,柔轮的等效应力呈现逐渐减小的趋势。其中,长径比在0.7~0.8时,柔轮应力下降更加明显;长径比从0.5增加到1时,柔轮的应力从1 050 MPa下降到631 MPa,下降了39%。
4.2 壁厚对对柔轮应力分布的影响
筒体的壁厚太大会导致柔轮局部应力变大;而当筒体的壁厚太小时,柔轮在工作过程中也容易发生疲劳断裂。
在保证柔轮其他参数不变的前提下,笔者仅仅通过改变柔轮的壁厚,建立起壁厚范围在0.7~1.2内的谐波减速器有限元模型。
筒壁厚度对柔轮应力影响的仿真结果如图12所示。

图12 筒壁厚度对柔轮应力的影响
从图12可知:随着柔轮的壁厚值逐渐增大,柔轮的等效应力也逐渐增大,但增加的趋势逐渐变小,最后趋于稳定在960 MPa左右。
由此可见,在实际工作中,在避免壁厚太小易断裂前提下,应当适当选择壁厚的数值。
4.3 齿宽对柔轮应力分布的影响
柔轮的齿宽是设计谐波减速器重要的一部分,增大齿宽能适当增加柔轮整体刚度,但齿宽的设计同样对波发生器的宽度存在影响,齿圈宽度的设计需要在设计范围之内。
在保持柔轮其他参数不变的基础上,笔者建立谐波减速器不同齿宽的有限元模型。
齿宽对柔轮应力影响的仿真结果如图13所示。

图13 齿宽对柔轮应力的影响
由图13可知:随着齿宽的增加,柔轮的等效应力随之增大;当齿圈从10 mm增加到15 mm,应力由550 MPa增加到967 MPa,增加了43%。该结果说明,齿圈的宽度对柔轮等效应力影响比较大。
5 结束语
本文针对渐开线谐波齿轮装配下的接触展开了分析,对不同参数装配下的柔轮应力进行了仿真分析,为谐波减速器柔轮的优化设计提供了参考。研究结论如下:
(1)柔轮装配波发生器后,柔轮筒体受到的变形主要在波发生器长轴处,沿轴向方向筒体变形量逐渐减小;在空载情况下,柔轮应力的分布及大小主要和波发生器有关,且齿圈处所受的应力最大,筒体所受的应力随着轴向方向逐渐减小;
(2)柔轮空载时,其应力上下左右对称,柔轮负载时最大应力发生偏移,方向为扭矩方向;且负载越大,柔轮整体应力越大;
(3)柔轮空载情况下,随着长径比的增大,柔轮的应力逐渐减小,而柔轮长径比越小,柔轮结构紧凑越符合轻量化设计要求;随着齿宽和筒体厚度的增大,柔轮的应力也逐渐增大,但筒体厚度与齿宽的值也不宜选择太小,应适当取值。
由于国内对工业机器人谐波减速器的研究尚处于发展阶段,此次相关的实验装置还在研究中,未进行实验测试。下一阶段的工作,即要采用相关实验装置进行实验测试。

