矿井电力线对信号电缆串扰的不确定度量化

刘 青， 丁 楠， 李艾娣， 杨佳仪， 周宁馨

(西安科技大学电气与控制工程学院， 陕西 西安 710054)

1 引言

煤矿井下空间狭小、机电设备相对集中，导致井下动力线和监控系统信号电缆间距离较近。当井下机电设备产生电磁骚扰或有雷电波入侵时，电力线上的各种骚扰会在信号电缆上感应出电流和电压，甚至可能完全覆盖来自各传感器的安监信号，从而导致信息失真，造成严重后果[1-3]。

针对矿井下电磁兼容的问题，多位学者展开了相关研究。文献[4]应用时域有限差分法(FDTD)对矩形巷道内传输线上的浪涌脉冲产生的电磁辐射场进行了建模研究；文献[5]建立了煤矿井下动力线与信号电缆的多导体传输线模型，应用FDTD方法研究了设备正常工作及开关操作瞬间安监信号回路的干扰数值；文献[6]建立了煤矿钢丝绳监测系统的多导体传输线模型，并进行了耦合规律研究。上述研究中，信号电缆多使用裸导线模型，实际上煤矿井下的信号电缆多采用屏蔽电缆。在建模方法上屏蔽电缆与裸导线有很大的不同，从而使计算结果也会与实际有所偏差，因此研究屏蔽电缆串扰问题有着实际应用价值。

此外，针对屏蔽电缆串扰的建模求解问题也有一些相关研究。文献[7，8]应用传输线理论对电缆结构进行等效处理，视电缆屏蔽层为多导体传输线中的一根子导线。文献[9]将屏蔽电缆场线耦合模型等效为两个通过转移阻抗和转移导纳建立联系的内、外传输线系统。但上述文献大都集中研究确定输入参数下的屏蔽电缆串扰响应结果。实际上，随着煤矿井下电磁环境和屏蔽信号电缆结构的复杂化，屏蔽信号电缆串扰响应中变量的不确定性总是存在的，因此固定变量对串扰的影响规律不够全面。

对于不确定性问题的分析，传统的方法是蒙特卡罗方法(MC)，该方法计算效率低，近年来产生了随机配点法(SC)、随机降阶法(SROM)、多项式混沌展开法(PCE)等高效方法对各种电磁兼容问题进行不确定度量化[10-12]。

本文将针对典型的矿井电力线和信号电缆的布置情况，应用FDTD方法计算电力线浪涌对信号电缆的串扰(信号电缆上的电压响应)。基于多项式混沌展开方法对串扰信号进行不确定度量化。本文中的不确定度量化充分考虑了输入参数变化对结果的影响，相对于固定输入条件下的输出结果，得到的规律更全面。本文中的方法相对于传统的蒙特卡洛方法，计算效率更高，而且能够和方差分解法相结合，分析输出结果对输入变量变化的敏感度。本文研究结果可对煤矿井下信号电缆的电磁干扰建模计算及防护提供参考。

2 电力线对信号电缆的串扰模型

电力线和信号电缆的传输线串扰模型分成内、外两个传输线系统。信号电缆屏蔽层外表面、电力线和大地构成外传输线系统，信号电缆屏蔽层内表面和芯线构成内传输线系统，内、外传输线系统通过转移阻抗和转移导纳建立联系。

2.1 外传输线系统

电力线对信号电缆的传输线串扰模型如图1所示。在外传输线系统中，将屏蔽信号电缆视为一根实心导体传输线。

图1 电力线对信号电缆的传输线串扰模型Fig.1 Transmission line model for crosstalk of power line to signal cables

在忽略分布电阻和分布电导的情况下传输线方程表示为：

(1)

(2)

式中，VS、IS分别为屏蔽层外表面上的电压(V)和电流(A)；L、C分别为传输线单位长度的分布电感(H)和分布电容(F)。

末端条件表示为：

V1=VS-RSIS

(3)

VNdz+1=VL+RLIL

(4)

式中，RS和RL分别为首端和末端的阻抗(Ω)；结合电力线与信号电缆的末端条件可得电力线和信号电缆屏蔽层外表面末端响应迭代公式：

(5)

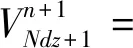
(6)

式中，VSS为电力线上的集总电压源(V)；V1为近端的电压响应(V)；VNdz+1为远端的电压响应(V)。

2.2 内传输线系统

将感应分布电压通过转移导纳等效为内传输线系统的分布电流源，转移导纳非常小，对计算结果影响较小，此处忽略不计。因此可以得到内传输线系统传输线方程：

(7)

(8)

式中，VSi为单位长度等效电压(V)；Li、Ci分别为屏蔽电缆芯线的单位长度电感(H)和电容(F)参数，计算公式参考文献[13]。

电缆内传输线的激励可以由式(9)确定。

Vsi=ZtIS

(9)

式中，IS为通过外传输线系统求解得到的屏蔽层外表面上的电流(A)；Zt为屏蔽电缆编织层的转移阻抗(Ω)。

本文引用了文献[14]中转移阻抗的模型：

Zt=Zd+jω(Mh±Mb)

(10)

式中，Zd为转移阻抗的散射部分，表示瞬态电磁场辐射到编织层上的低频特性；Mh为小孔电感，由小孔耦合引起；Mb为网孔电感，由编织束编进编出，切割编织层间隙的磁力线引起。

3 单个变量对串扰的影响规律分析

3.1 计算条件

3.1.1 矿井浪涌骚扰的来源及标准

浪涌(冲击)骚扰是国家电磁兼容标准中对电子设备危害较大的典型瞬态电磁骚扰之一。一般分为外部浪涌和内部浪涌两种。由于煤矿供电系统在电源入井口处采取了防雷措施，所以雷电产生的外部浪涌基本上不会对井下的电力系统造成影响。而与矿井电力系统内部的设备开关动作和供电网络运行的故障有关的内部浪涌才是矿井浪涌骚扰的主要来源。

根据国际标准IEC 61000-4-5和国家标准GB/T 17626.5的相关规定，同时结合实际井下设备电力线对安监信号电缆干扰的具体情况，选取标准的1.2/50 μs的浪涌电压作为干扰源。

VSS(t)=AVp(1-e-t/τ1)e-t/τ2

式中，τ1=0.407 4 μs；τ2=68.22 μs；A=1.037。

3.1.2 矿井电力线和信号电缆的布局

煤矿井下电力线与信号电缆通常采用单端布局和双端布局两种情况，如图2所示。

图2 电力线与信号电缆布局示意图Fig.2 Schematic of layout of power lines and signal cables

布局不同导致在两种布局情况下电缆单位长度电容求解方式不同。两端布局下电缆间单位互电容求解表达式如式(11)，但是单端布局下电缆间单位互电容求解表达式如式(12)所示。

(11)

(12)

式中，hg为动力电缆离地高度(m)；hr为信号电缆离地高度(m)；d为两电缆间间距(m)。

3.1.3 参数设定

考虑实际情况，设定浪涌脉冲幅值Vp为1 000 V。图1中电力线、信号电缆长度均为8 m；电力线和信号电缆芯线末端均接匹配电阻50 Ω；信号电缆屏蔽层两端通过匹配电阻50 Ω接地；电力线直径为0.8 mm；信号电缆选用MSYV同轴电缆，其屏蔽特性参数见文献[15]。

信号电缆首末端有无屏蔽层干扰电压幅值如图3所示。从仿真结果可以看出无屏蔽层的感应电压比有屏蔽层明显大近一个数量级，因此针对裸导线的分析结论对实际的指导作用不足。

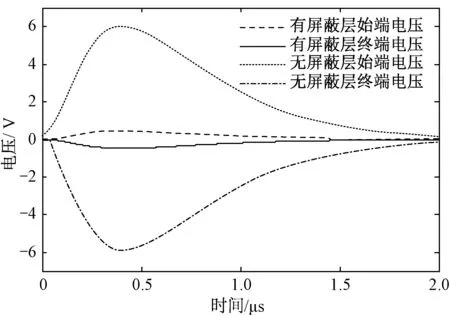
图3 信号电缆首末端有无屏蔽层干扰电压对比图Fig.3 Comparison of interference voltage of braided layer at beginning and end of signal line

3.2 给定单变量规律计算

3.2.1 编织层夹角对响应电压的影响

屏蔽层编织角的不同会影响屏蔽电缆的转移阻抗，进而影响串扰响应结果。改变信号电缆屏蔽层编织角，计算结果如图4所示。可见，两种布局情况下响应电压(为表述方便，以下用VNEXT、VFEXT分别表示信号电缆首末端电压)随着屏蔽层编织角的增加先变小后增大，在65°到70°出现最小拐点。这是因为当编织层夹角约为65°时转移阻抗为最小值，即式(9)信号电缆芯线上感应的分布电压源最小，最终导致响应电压最小。

图4 不同编织线夹角下VFEXT幅值Fig.4 Magnitudes of VFEXT under different braided wire angles

3.2.2 电力线离地高度对响应电压的影响

改变电力线离地高度，计算结果如图5所示。可见，信号电缆末端响应电压会随着电力线离地高度的增加而增加；两种布局增加的趋势略有不同。这是因为两种布局下电容参数计算公式虽略有不同。但其整体都是随高度增加而增加，所以结果呈现略有不同的递增趋势。

图5 不同离地高度下VFEXT幅值Fig.5 Magnitudes of VFEXT under different ground heights

3.2.3 线间间距对响应电压的影响

考虑到实际巷道尺寸不固定，两端布局中将电力线与信号电缆的间距取巷道的宽度范围，单端布局中间距取巷道的高度范围。间距变化对电压响应的影响如图6所示。可见，两端布局时，串扰电压峰值随电缆间间距的增加线性减少；单端布局时，串扰响应电压峰值随电缆间间距递减的程度呈现递减趋势，与两端布局的变化规律不同。

图6 不同信号电缆与电力线间距下VFEXT幅值Fig.6 Magnitudes of VFEXT under different spacing

可见，信号电缆串扰响应随着动力电缆离地高度的增加而增加；随电缆间间距的增加而减小；随着编织层夹角的增大而先减小后增大，在65°～70°出现最小拐点。两种布局下由于相关参数计算公式的不同使得影响规律略有不同，但两者之间无关联。

4 屏蔽电缆串扰的不确定度量化

本节针对屏蔽层编织角、电力线与信号电缆的间距以及信号电缆对地高度三个不确定输入变量同时变化情况进行计算研究。

4.1 屏蔽电缆串扰的混沌多项式展开

多项式混沌展开法是利用一组正交多项式方程代理原模型的响应函数。将屏蔽信号电缆编织层夹角、线间间距和传输线离地高度看作三维随机输入变量，用ξ={ξ1,ξ2,ξ3}表示，将屏蔽电缆串扰电压时域峰值的绝对值作为输出变量，基于PCE方法，输出变量可表示为：

(13)

式中，Y为拟合函数输出响应(即信号电缆串扰响应最大值)；ai(i=0,1,2,…,p)是多项式混沌展开系数；ξ={ξ1,ξ2,ξ3}为3维随机变量；ψi(ξ)是以随机变量ξ为参量的3维正交多项式基底；p为截断阶数。

步骤1：根据屏蔽信号电缆编织层夹角、线间间距和传输线离地高度服从的分布类型，确定该分布类型下的正交多项式基底。

对于服从常见标准分布类型的随机变量，根据Askey方案可以查找到最优基底函数。本文随机变量分布类型设定为标准均匀分布，使用Legendre多项式(L)一维正交多项式基底：

(14)

多维正交多项式ψi(ξ)可以表示为多个一维正交多项式的乘积，对于“全阶展开法”相应的d阶PCE模型中ψi(ξ)可以表示为：

(15)

步骤2：利用随机响应面法，求解混沌多项式展开系数。

对于“全阶展开法”相应的d阶PCE模型中PCE系数的个数Q随着PCE模型的阶数d和随机变量ξ的维数n的增长而增加，设定变量ξ的维数n=3。具体函数关系由式(16)确定。

(16)

最后利用最小二次回归估计PCE系数：

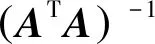
(17)

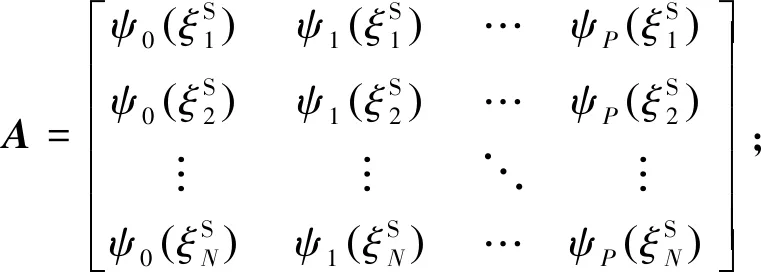
式中，A是3维正交基底函数。

步骤3：结合正交多项式基底ψi(ξ)和PCE系数αi得到屏蔽电缆串扰响应代理模型，将随机变量的样本数据直接输入代理模型中对串扰响应进行统计分析。

4.2 不确定度量化分析结果

算例参数：动力电缆、信号电缆长度均为8 m，动力电缆和信号电缆芯线末端均接匹配电阻50 Ω，信号电缆屏蔽层两端通过匹配电阻50 Ω接地，动力电缆直径为0.8 mm，信号电缆选用MSYV同轴电缆，同时考虑线间间距、电缆离地高度和信号电缆编织层夹角的不确定性，线间间距、电缆离地高度和信号电缆编织层夹角服从表1的分布区间。

表1 两种布局下串扰模型不确定参数的分布区间Tab.1 Distribution interval of uncertain parameters of crosstalk model under two layouts

当线间间距、电缆离地高度和信号电缆编织层夹角同时为不确定性参数时，两端布局下信号电缆末端响应电压幅值的累积概率分布曲线如图7所示。可见，当PCE采样点为20个时，信号电缆末端响应电压的累积概率分布曲线与MC计算结果的吻合度较好，采样点为40、70时可以看到与MC方法的吻合度更好。

图7 两端布局下VFEXT幅值的累积概率密度曲线Fig.7 Cumulative probability density curve of magnitudes of VFEXT under layout of both ends

表2为两端布局下信号电缆末端电压的统计信息。可见，对于内存为4 GB，64位操作系统的计算机，传统蒙特卡罗方法10 000采样点MATLAB程序运行时间为21 163 s，统计得到信号电缆末端电压幅值的均值和标准差为0.343 4 V、0.005 8 V；而3阶40采样点的PCE方法MATLAB程序运行时间为152 s，计算得到信号电缆末端电压幅值的均值和标准差为0.344 2 V、0.076 4 V。因此说明PCE方法在满足计算结果的精确度条件下计算效率远大于MC方法。同样情况下，单端布局时信号电缆末端电压的累积概率密度曲线如图8所示。两种布局情况下响应电压的统计信息如表3所示。

表2 末端电压幅值的统计信息(两端布局)Tab.2 Statistics of voltage amplitude at first end (layout at both ends)

图8 单端布局下VFEXT幅值的累积概率密度曲线Fig.8 CDF of magnitudes of VFEXT under single-ended layout

表3 信号电缆首末端电压幅值的统计信息Tab.3 Statistics of terminal voltage amplitude

图9给出了不同布局情况下，信号电缆末端响应电压的频次图。可见，两端布局下最易出现的末端电压幅值为0.363 9 V附近的区域，单端布局下最易出现的末端电压幅值为0.927 7 V附近的区域。

图9 不同布局下VFEXT幅值频次图Fig.9 Frequency diagram of VFEXT under different layouts

4.3 敏感度分析

为了定量分析各随机输入变量对信号电缆串扰响应的影响程度，基于方差分解法对参数的敏感度进行分析。d阶多项式混沌展开式如下：

(18)

式中，ξ=(ξ1,ξ2,…,ξn)；ψi1,…,id(ξi1,…,ξid)是以不确定参数ξi1,…,ξid为变量的d阶正交多项式基底；αi1,…,id为与之对应的多项式混沌展开式系数。

对式(18)左右两边求方差，并结合方差分解法可得到参数xi的总敏感度指标SiT：

(19)

利用式(19)计算得到信号电缆浪涌脉冲响应对三维输入变量的敏感度指标，其柱状图如图10所示。

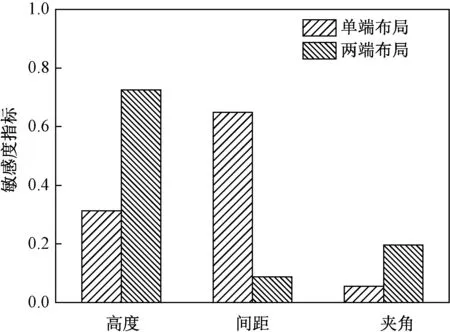
图10 VFEXT幅值对不同参数的敏感度Fig.10 Sensitivity of magnitudes of VFEXT to different parameters

从图10中可以看出编织层夹角在单端布局下对信号电缆浪涌脉冲响应的影响较小，线间间距在两端布局下对信号电缆浪涌脉冲响应的影响较小，传输线离地高度在单端布局下对信号电缆浪涌脉冲响应影响较小。即编织层夹角在单端布局下对信号电缆浪涌脉冲响应的影响较小，可将其取为确定值，从而降低不确定参数的维度，化简多维不确定度量化问题的复杂度；同理，线间间距在两端布局下对单端布局下监测信号电缆浪涌脉冲响应的影响较小，可将其取为确定值，从而降低不确定参数的维度，化简多维不确定度量化问题的复杂度。

为验证上述结果的正确性，在单端布局情况下，图11分别对输入变量的四种处理方法进行仿真计算。可以发现，忽略编织层夹角的不确定性同考虑三维变量之间的累积概率分布区别最小，因此验证单端布局情况下编织层夹角的敏感度较小的结论。

图11 单端布局情况下累积概率分布对比图Fig.11 Comparison of cumulative probability under single-ended layout

5 结论

本文建立了矿井下电力线对信号电缆的串扰计算模型，考虑到输入变量的不确定性基于PCE方法对信号电缆上的串扰电压进行了不确定度量化。得到以下结论：

(1)信号电缆末端响应电压随线间距增大而减小，随传输线离地高度增大而增大，随编织层夹角的增加先减小后逐渐增大，在65°～70°出现一个最小干扰极值拐点。

(2)PCE方法能准确有效地反映输入变量变化引起的串扰响应的不确定度，且计算效率明显高于MC方法。

(3)通过不确定度量化分析，可得到信号电缆末端响应的均值、标准差和置信区间等统计信息，同时发现单端布局下的串扰电压要高于两端布局的串扰电压。

(4)单端布局时，信号电缆末端响应电压对电缆线间距最为敏感，对电力线高度次之，对电缆编织层夹角最不敏感；两端布局时，信号电缆末端响应电压对电力线高度最为敏感，对电缆间距最不敏感。