关于丢番图方程（24n）x＋（143n）y＝（145n）z

冉银霞

（陇南师范高等专科学校数信学院，甘肃 成县742500）

引言

设a，b，c为两两互素的正整数且满足a2＋b2＝c2。对于任意的正整数n，丢番图方程

显然有正整数解（x，y，z）＝（2，2，2）。当n＝1时，在文献［1-2］中，证明了当

（a，b，c）＝（3，4，5），（5，12，13），（7，24，25），（9，40，41）或（11，60，61）时，方程（1）都仅有整数解

（x，y，z）＝（2，2，2）的结论。当n为任意正整数时，在文献［3-16］中，证明了当

（a，b，c）＝（3，4，5），（5，12，13），（7，24，25），（9，40，41），（11，60，61），（13，84，85），（15，112，113），（8，15，17），（12，35，37），（20，21，29），（28，45，53），（36，77，85），（65，72，97），（44，117，125），（22r-1，2r＋1，22r＋1）（r∈N*），（48，55，73），（60，91，109），（56，33，65），（80，39，89）或（20，99，101）时，方程（1）都仅有正整数解（x，y，z）＝（2，2，2）的结论。至此，max｛a，b，c｝＜130，n为任意正整数的情形已全部解决。

另外，针对方程（1），胡邦群［17］对a-b＝m（m≡7，3，5（mod8）），n＝b，m■n这些情况，找到了一些Jesmanowicz猜想成立的n。苟莎莎［18］对a-b＝m（m≡7，3，5（mod8））的情形，证明了若m≡3，5（mod8），m含模8余3的因子，则当2n＋m不含4k＋1型素因子时，Jesmanowicz猜想成立。杨海等［19］证明了方程（1）没有满足max｛x，y｝＞min｛x，y｝＞z及n＞1的解，尤其a＝p（p为奇素数），b＝2时，方程（1）没有满足x＞z＞y及n＞1的解；杨海等［20］证明了

定理1对任意的正整数n，丢番图方程

仅有正整数解（x，y，z）＝（2，2，2）。

1 若干引理

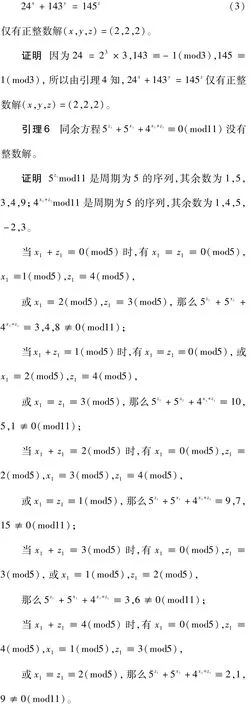
综上，同余方程5z1＋5x1＋4x1＋z1≡0（mod11）没有整数解。

2 定理的证明

143y＝nz-y（145z-24xnx-z） （4

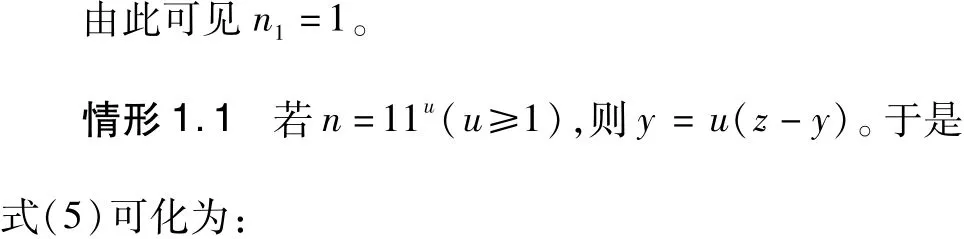
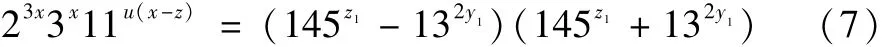
对式（8）取模4，有1-（-1）y≡0（mod4），得y≡0（mod2）；

23x3x13v（x-z）＝（1452z1-112y1）（1452z1＋112y1）（9）

若z＞3x，则2z-3x≡1（mod143），于是120｜（z-3x）且x为偶数，则6｜z.设x＝2x1，z＝6z1，因此

3 结束语

学者们已对n为任意正整数，max｛a，b，c｝＜130的情形，证明了Jes＇manowicz猜想成立。实际上，经简单计算可知，当130＜max｛a，b，c｝＜150时，可讨论的情形只有5种，即（a，b，c）＝（44，117，125），（88，105，137），（24，143，145），（140，51，149）或（144，17，145）这5种。本文证明了其中之一，即当（a，b，c）＝（24，143，145）时，Jesm＇anowicz猜想成立。