铜期权隐含波动率曲面拟合方法比较

张不凡

摘 要：本文以上海期货交易所的铜期权为研究对象，对不同隐含波动率曲面模型的拟合精度和不同市场情况下的适用性进行了实证对比。从实证结果来看，SABR模型的拟合精度最高且对不同市场情况都有较好地刻画，而二次多项式模型和VGVV模型的拟合误差相对较大。SSVI模型的拟合精度略低于SABR模型，但在拟合速度和參数稳定性上更有优势且对于数据要求相对较低。在实际应用中，可根据实际市场情况和数据质量，结合SABR和SSVI两种模型得到适合的隐含波动率曲面。

关键词：铜期权 隐含波动率曲面 拟合精度

一、引言

近年来，我国商品期货市场陆续推出了多个商品期货、期权，为广大投资者提供了更多套期保值和投资工具。期权非线性的价格蕴含着丰富的市场预期信息，其中最为重要的是期权的隐含波动率。与基于期货历史数据外推预测的波动率相比，期权隐含的波动率信息更具前瞻性和真实性。在同一剩余期限上，不同在值程度的隐含波动率的变化反映了标的资产收益率分布的非正态性，形成了通常所说的波动率微笑或偏斜;而相同在值程度的隐含波动率在不同剩余期限上的变化则反映了不同期限收益率非正态性分布的变化，形成了隐含波动率期限结构。隐含波动率在不同在值程度和剩余期限的变化，即形成所谓的隐含波动率曲面。

在实务中，期权做市商需要根据隐含波动率曲面对期权进行报价，而其作为度量波动率风险的重要工具，也是期权交易者对冲波动率风险以及风险管理者构建风险压力场景所必需的。因此拟合构建合理的隐含波动率曲面，对于期权的定价、交易和风险管理都有着重要的意义。本文以上海期货交易所的铜期权为研究对象，对几个主要的隐含波动率曲面拟合方法进行实证比较和适用性探讨。

二、隐含波动率曲面拟合方法

目前在学术研究和业界的实务应用中，构建隐含波动率曲面的常用模型方法主要有二次多项式模型、SABR（Stochastic-Alpha-Beta-Rho）模型、SSVI（Surface Stochastic Volatility Inspired）模型和VGVV（Vega-Gamma-Vanna-Volga）模型。下面首先对这四种模型分别进行介绍，然后选取铜期权数据进行隐含波动率曲面拟合。

（一）二次多项式模型

二次多项式模型是在波动率曲面早期研究中一种简单且应用较为广泛的参数模型，该模型直接对隐含波动率的对数建模，将其表示为在值程度和剩余期限的代数多项式形式。具体地，二次多项式表示的隐含波动率曲面通常具有如下的形式（Dumas et al，1998）。

lnσt（k，τ）=β1+β2k+β3k2+β4τ+β5kτ（1）

其中，k=ln（K/F）为期权的对数化在值程度，τ为剩余期限，σt（k，τ）即为在值程度为k、剩余期限为τ的期权隐含波动率。二次多项式模型为波动率曲面模型，共有5个参数{β1，β2，β3，β4，β5}，可以用每日各期限、各行权价的隐含波动率作为输入变量，进行线性最小二乘校准参数，参数值并不依赖初始值，参数估计过程简便、稳定。但值得注意的是，二次多项式模型并不保证满足任何无套利条件。

中国证券期货2021年3月

第1期铜期权隐含波动率曲面拟合方法比较

（二）SABR模型

SABR模型由Hagan等（2002）提出，由标的远期在远期测度下的随机过程出发，通过期权定价公式推导出隐含波动率公式，模型天然无套利，不必额外施加无套利约束条件。模型最一般的随机过程假设为dFt=σtFβtdzFt，在实际使用中通常假设标的资产遵循几何布朗运动，即令β=1，dFt=σtFβtdzFt，模型简化为

其中，k=ln（K/F）为对数化在值程度，τ为剩余期限，z=-ναk，χ（z）=log1-2ρz+z2+z-ρ1-ρ。模型中共有3个待估参数{α，ρ，ν}，其中α为随机过程假设的波动率初始值，ρ为标的资产与波动率的相关系数，ν反映的是波动率的波动。参数约束条件为α>0，-1≤ρ≤1，ν>0。

SABR模型本质上是波动率微笑模型，需要在期限结构上对总方差进行插值得到波动率曲面。可以用每日给定期限的期权的隐含波动率作为输入变量，进行非线性最小二乘校准参数。校准参数时需要进行最优化寻找全局最优解，参数值一定程度上依赖于初始值的设定。

（三）SSVI模型

SSVI模型是由SVI（Stochastic Volatility Inspired）模型拓展而来。SVI模型在波动率曲线拟合方面有着广泛的应用，但也有较为显著的缺点，即模型设定中缺少无套利约束条件。Gatheral和Jacquier（2014）针对该问题对SVI模型进行了改进，在模型设定中增加了无套利约束条件，并对整个隐含波动率曲面进行建模，由此提出了SSVI模型，其对隐含总方差w（k，θτ）的参数表达式的设定如下。

其中，k=ln（K/F）为对数化在值程度，θτ=σ2t（0，τ）τ为平价期权的隐含总方差，而w（k，θτ）为隐含总方差，反映了不同在值程度和剩余期限下的隐含总方差，从而刻画了整个隐含波动率曲面。在满足极限limτ→0θτφ（θτ）存在的条件下，通过对φ（·）设定不同的函数形式可产生具有不同性质的隐含波动率曲面，其中较为常用的函数形式为φ（θ）=ηθγ（1-θ）1-γ，本文的实证即采用该函数形式。SSVI模型共有三个参数{η，ρ，γ}，可以用每日各期限、各行权价期权的隐含波动率作为输入变量，进行非线性最小二乘校准参数。校准参数时需要进行最优化寻找全局最优解，参数值一定程度上依赖于初始值的设定。参数约束条件为η>0，-1≤ρ≤1，-1<γ<1。无蝶式、差期套利的约束条件为η（1+ρ）≤2。

（四）VGVV模型

VGVV模型由Carr和Wu（2016）提出，从标的资产的随机过程及隐含波动率的随机过程出发，在动态无套利条件下通过期权定价公式推导出了隐含波动率所满足的偏微分方程。期权的Theta和其他几个重要的希腊字母Vega、Gamma、Vanna、Volga由此统一聯系在偏微分方程中，因此该模型被称为VGVV模型。

假设隐含波动率It（k，τ）遵循比例型随机波动率曲面过程如下。

模型共有5个待估参数{η，w，m，ρ，ν}，参数约束条件为η，w，ν>0，-1≤ρ≤1。可以用每日各期限、各行权价期权的隐含波动率作为输入变量，进行非线性最小二乘校准参数。校准参数时需要进行最优化寻找全局最优解，参数值一定程度上依赖于初始值的设定。由于上述方程直接反映了无套利隐含波动率曲面应该具有的形状，因此不必额外施加无套利约束条件。给定{η，w，m，ρ，ν}的当前值，隐含波动率的解的形式如下。

本文以铜期权为研究对象进行实证比较。铜期权挂牌的合约月份为与铜期货相同的连续月份，由于铜期权的标的铜期货主力合约一般为近月合约，因此通常铜期权的当月合约最为活跃，第二个月和第三个月合约的成交活跃度依次减弱，自第四个月合约起成交十分稀疏，而后续月份的合约几乎少有成交。因此，我们取铜期权的前四个月合约的期权数据进行隐含波动率曲面拟合的实证比较。

本文通过Black模型由铜期权的每日收盘价推算出期权的隐含波动率，作为拟合波动率曲面的输入变量，即市场观测值。使用的实证数据包括铜期货、铜期权的日收盘价数据，样本期为2020年1月2日至2020年9月30日，数据来自上海期货交易所。无风险利率使用对应期权剩余期限的中债国债即期收益率，数据来自Wind。从市场实际交易情况来看，虚值合约的交易活跃度明显大于实值合约，因此对于行权价低于标的价格的，本文取虚值看跌期权合约来计算隐含波动率作为市场观测值，反之则取虚值看涨期权合约。同时，借鉴现有文献的常用做法，我们对原始的铜期权数据进行了筛选处理，以减少流动性风险、市场噪声和定价偏误等带来的影响。①剔除剩余期限小于或等于5个交易日的期权数据，期限很短的期权包含的时间价值或波动信息已经很少;②剔除收盘价格为1的合约，因为铜期权的最小变动价位为2，低于该价格的合约已难以反映其真实价格;③剔除违反期权理论价格上下限约束的不合理数据。

在实证比较中，本文首先针对不同市场情况（平稳、上涨、下跌）下，将各模型拟合的曲面进行举例分析，探讨其在不同市场情形下的适用性。然后进一步使用2个指标衡量波动率曲面拟合模型的整体拟合精度，模型拟合误差（V）和模型解释比率R如式（7）和式（8）所示。

其中，V（k，τ）为隐含波动率的市场观测值，V︿（k，τ）为隐含波动率的模型拟合值，k和τ分别为期权在值程度和剩余期限。因此，模型拟合误差即为隐含波动率的市场观测值与模型拟合值之间的误差，而模型解释比率则类似于线性回归中的R2，反映了能被模型解释的信息（方差）比率。实证中我们分别计算了不同在值程度和剩余期限下的模型拟合误差和模型解释比率，考察各波动率曲面模型在不同在值程度和剩余期限上的拟合效果。

四、实证比较结果

（一）不同市场条件下的拟合曲面比较

在使用模型拟合误差和模型解释比率两个指标对各模型对波动率曲面的拟合精度进行整体比较前，我们首先对各模型在不同市场条件下对波动率曲面的拟合情况做一下直观的比较。

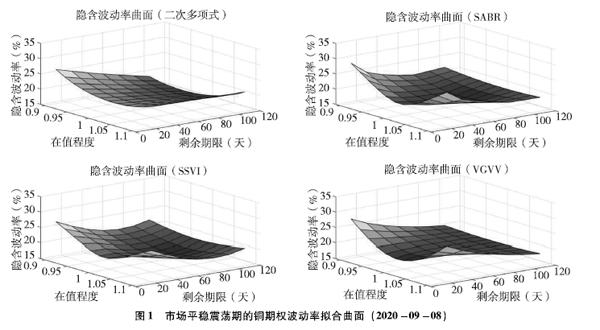
图1、图2和图3分别是市场平稳震荡期间（样本为2020年9月8日）、市场上涨期间（样本为2020年7月13日）和市场下跌期间（样本为2020年3月16日）各模型拟合的波动率拟合曲面。从图中可以看出，各模型拟合的波动率曲面都能在大致形态上反映出波动率在不同在值程度和不同期限上的变化，即通常所说的波动率微笑和波动率期限结构。

1市场平稳震荡期

在市场平稳震荡期，波动率曲面通常在较短期限呈现较为标准的波动率微笑，而随着剩余期限的加长，波动率微笑逐渐趋于平坦。比较各模型拟合的波动率曲面（见图1）可以看到，其中二次多项式模型的曲面虽然整体光滑，但其在各期限都是标准的波动率微笑，丢失了波动率在期限结构上的变化细节;而VGVV模型在长期限处的波动率曲面则过于平坦;相比之下，SABR模型和SSVI模型对于波动率曲面的刻画更为细致准确。

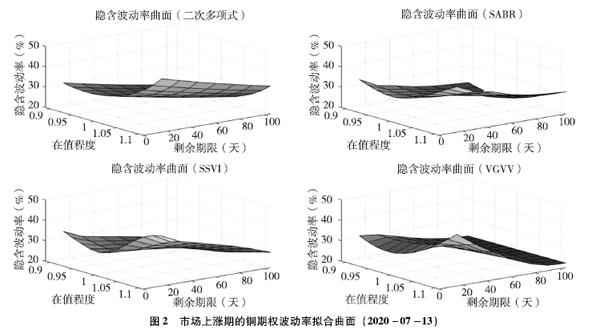
2市场上涨期

在市场上涨期，波动率曲面通常呈现稍显右偏（正偏）的波动率偏斜，并随着剩余期限的增长趋于平坦。从图2中可以看到，与市场平稳期类似，二次多项式模型的曲面在各期限上的波动率偏斜形态并没有太大变化，丢失了较多细节;VGVV模型在短期限处的波动率偏斜有较好刻画，但在长期限处仍过于平坦;同样地，SABR模型和SSVI模型对于市场上涨期的波动率曲面刻画更为准确。

3市场下跌期

在市场下跌期，波动率曲面经常在短期限处呈现显著左偏（负偏）的波动率偏斜，随着剩余期限的增长虽有平缓，但在较长期限处仍有较为明显的波动率偏斜存在。从图3中可以看出，二次多项式模型的曲面在长期限处的波动率偏斜形态变化不大，同样未体现出波动率在期限结构上的变化;而其他三个模型整体上对波动率偏斜和波动率期限结构上的变化有较好地刻画。值得注意的是，SSVI模型的波动率拟合曲面对于左尾处（在值程度为085）的波动率有明显的偏差，相对于其他模型低估了左尾处的波动率（该样本下近月合约的左尾波动率达到了60%左右，而SSVI模型拟合波动率曲面后，其模型的左尾波动率只有40%左右）。由此可见，在市场有较大波动时，SSVI模型对于深度虚值处有相对较大的拟合误差。

（二）模型整体拟合精度比较

1二次多项式模型

二次多项式模型最大的特点是参数校准简单方便，无须最优化，参数值不依赖于初始值的设定，因此模型拟合非常快速。但我们从表1中的模型拟合误差均值和模型解释方差比率可以看到，二次多项式模型仅对短期限的期权的拟合误差均值相对较小，在2%左右，模型解释度普遍在80%以上。但对于中期限和长期限的期权，二次多项式拟合的波动率误差陡然上升，都达到了3%以上，部分深度虚值期权对应的波动率误差均值甚至超过了10%，对应的模型方差比率也大多为负值。

虽然二次多项式模型在计算上快速方便，但其对波动率曲面的拟合误差均值偏大，这令其在实际使用中很难满足精度要求。

2SABR模型

与二次多项式模型单纯的数据拟合不同，SABR模型本质上是随机波动率模型，富有经济意义。在拟合时SABR模型要对期权的每个期限刻画一条单独的波动率曲线，每条波动率曲线需要校准的待估参数有3个，这要求每条波动率曲线上至少有4个数据质量较好的点。因此如果遇到交易不活跃的情况，可能会导致SABR模型无法正常校准参数。从实证使用的铜期权数据来看，基本能够符合数据要求。

从实证数据来看，SABR模型需要每日拟合4条波动率曲线，每条曲线在参数校准时需要进行最优化，因此普遍耗时较长，模型计算速度相对较慢，但在可接受范围之内。表2为SABR模型对样本数据拟合波动率曲面的模型拟合误差均值和模型解释方差比率。从拟合误差来看，SABR模型对短中期剩余期限的波动率拟合误差均值都较小，多在05%左右，对于较长剩余期限的波动率拟合误差均值也在1%左右，且其对虚值程度较深的波动率拟合误差均值也没有显著增大。而从模型解释方差比率来看，对于不同在值程度和剩余期限，SABR模型拟合曲面计算的波动率都有着很高的模型方差解释比率，绝大多数都达到了95%以上。

因此，虽然SABR模型由于所需最优化次数较多，在拟合效率上有所欠缺，但从其模型拟合误差均值和模型解释方差比率来看，有着很好的模型精度，远超二次多项式模型。

3SSVI模型

SSVI模型在刻画每日的波动率曲面进行参数校准时同样需要最优化，但与SABR模型不同的是，SSVI模型是直接对整个曲面进行参数校准，不需要对不同期限的每条波动率曲线分别校准，因此普遍耗时较SABR模型更短，模型计算速度快。SSVI模型有3個待估参数用于波动率曲面校准，因此理论上要求输入模型的数据在所有期限的波动率曲线上达到至少4个即可，除非遇到交易极度不活跃的情况，否则一般都可以满足，其对模型的数据要求较SABR模型降低不少。

表3为SSVI模型对样本数据拟合波动率曲面的模型拟合误差均值和模型解释方差比率。从拟合误差均值来看，SSVI模型对短、中和较长期限的浅虚值（在值程度为095～105）的波动率拟合误差均值都相对较小，基本在1%以内;而随着虚值程度的逐渐加深，其波动率拟合误差均值也随之增大，在深度虚值处达到了3%以上。从模型解释方差比率来看，除深度虚值以外的波动率，模型在不同剩余期限上都有着较好的模型解释方差比率，多数都在90%以上，而曲面在深度虚值处拟合的波动率的模型解释方差比率较低。

因此，从模型拟合误差均值和模型解释方差比率来看，SSVI模型对在值程度在09～11区间的浅虚值和虚值的波动率拟合精度较好，但对深度虚值的波动率拟合有明显的误差，整体上拟合误差大于SABR模型。而从拟合效率来看，由于SSVI模型对数据要求较低，其拟合速度和参数稳定性都优于SABR模型。

4VGVV模型

VGVV模型在拟合波动率曲面进行参数校准时也是对整个曲面进行校准，而不需要拟合每条波动率曲线，其待校准的参数为5个，其模型拟合的稳定性和时间效率存在一定问题，在实际测算中，也发现其拟合波动率曲面的平均耗时显著高于SABR模型和SSVI模型。

表4为VGVV模型对样本数据拟合波动率曲面的模型拟合误差均值和模型解释方差比率。从拟合误差均值来看，VGVV模型对短期限的波动率拟合误差均值相对较小，平均在1%左右;而剩余期限的拉长，其波动率拟合误差也随之增大，在中长期剩余期限的波动率拟合误差在2%左右。从模型解释方差比率来看，模型在短期限上有着较好的模型解释方差比率，但在中长期剩余期限下的模型解释方差比率大多相对较低。

因此，在实证中VGVV模型拟合的波动率曲面在短期限上有不错的拟合精度，但在中长期期限上，VGVV模型的拟合精度相对较差一些，拟合误差均值和解释方差比率较SABR和SSVI模型都稍逊一筹。

五、总结

本文以铜期权为研究对象，对二次多项式模型、SABR模型、SSVI模型和VGVV模型的拟合精度和在不同市场情况下的适用性进行了实证对比，表5给出了各模型拟合效果的对比结果。

虽然从拟合效率来看，二次多项式模型最为快速稳定，但其刻画的波动率曲面在期限结构的变化上丢失了较多细节，相比其他几个模型存在较大的拟合误差，使其难以运用到实际市场中。

近年提出的VGVV模型虽然在理论上最富有经济意义，但从实证结果来看，其在较长期限处的拟合误差均值相比SABR和SSVI较大，同时其在拟合速度和参数稳定性上也存在一定问题，整体上有着明显的劣势。

SABR模型和SSVI模型在拟合精度和拟合效率上都有着较好的效果，其中SABR模型在拟合精度上更好，SSVI模型则在拟合速度和参数稳定性上更有优势。从模型设定上看两者都满足无套利条件，SABR模型本质上是随机波动率模型，相比纯数据拟合的SSVI模型更具有经济意义，而SSVI模型则对于数据要求相对较低。因此在实际应用中，可根据市场情况和数据质量，结合两种模型得到最适合的隐含波动率曲面。

參考文献

[1]赵永杰期权隐含跳跃风险及风险溢酬——基于动态无套利波动率曲面模型的分析[D]厦门：厦门大学，2017

[2]赖明潭铜期权波动率探讨与分析[J]中国证券期货，2019（2）：40-44

[3]DUMAS B，FLEMING J，WHALEY R EImplied volatility functions： empirical tests[J]The Journal of Finance，1998，53（6）：2059-2106

[4]HAGAN P S，KUMAR D，LESNIEWSKI A S，WOODWARD D EManaging smile risk[J]Wilmott Magazine，2002，1：84-108

[5]GATHERAL J，JACQUIER AArbitrage-free SVI Volatility surfaces[J]Quantitative Finance，2014，14（1）：59-71

[6]CARR P，WU LAnalyzing volatility risk and risk premium in option contract： a new theory[J]Journal of Financial Economics，2016，120（1）：1-20

[7]BLACK FThe pricing of commodity contract[J].Journal of Financial Economics，1976，3（1-2）：167-179