Continuous-variable quantum key distribution based on photon addition operation∗

Xiao-Ting Chen(陈小婷), Lu-Ping Zhang(张露萍), Shou-Kang Chang(常守康),

Huan Zhang(张欢)1, and Li-Yun Hu(胡利云)1,2,†

1Center for Quantum Science and Technology,Jiangxi Normal University,Nanchang 330022,China

2Key Laboratory of Optoelectronic and Telecommunication,Jiangxi Normal University,Nanchang 330022,China

Keywords: non-Gaussian operations, continuous variable, quantum key distribution, photon-addition opera

1. Introduction

Quantum key distribution (QKD)[1–5]has been considered to be an unconditional security scheme, which is protected by the quantum mechanics principle, such as the Heisenberg uncertainty principle[6]and the noncloning theorem.[7]Generally, there are two kinds of types for realizing the QKD proposal,i.e.,discrete variable(DV)QKD and continuous variable (CV) QKD.[8–15]In the CVQKD protocol, the information of key bits is usually encoded by Alice(the sender)in two quadrature components of the optical field,while for the DVQKD protocol,the information of key bits is transmitted by the polarization of a single photon. This point is different from each other. On the other hand,for the former,Bob (the receiver) at the recipient port can decode the secret information by using high-speed and high-efficiency coherent detections,instead of a single-photon detection used in the latter. Thus the CVQKD protocol can achieve higher secret key rates especially in short transmission distance. In addition,the CVQKD protocols are more compatible with most classical telecommunication technologies. Based on these two reasons,much attention has been paid to the CVQKD systems. However,the performance of CVQKD for long distances is unsatisfactory.

In order to eliminate the short-distance problem, many efforts have been devoted to improving the secure transmission distance of CVQKD and lots of remarkable progress have been made both theoretically[16]and experimentally.[17,18]For instance, due to the efficient error correction codes, the CVQKD protocols with the discrete modulation,[19,20]first proposed by Leverrier and Grangier theoretically,[21]can be used to improve the secure distance to a great extent under the condition of the low signal-to-noise ratio (SNR). In addition, when the discrete-modulated scheme is applied to the measurement-device-independent (MDI) CVQKD,[22]it is shown that the maximal transmission distance can be improved compared to that of the MDI CVQKD with the Gaussian modulation.[23]Here we should notice that, in these discrete-modulated CVQKD protocols,the corresponding security proofs have not been rigorously demonstrated both theoretically and experimentally, and a way equivalent to the Gaussian modulation is still employed under the condition of a very small modulation variance. Actually, in the conventional Gaussian modulation CVQKD,the security of CVQKD against collective attack[24]and coherent attack[25]has been proved theoretically, say the Gaussian-modulated coherent states CVQKD (i.e., the well-known “GG02” protocol).[26]Based on the Gaussian-modulation idea,a scheme of CVQKD with a multidimensional harmonic is proposed to improve the secure transmission distance.[27]In experiment,the field tests of CVQKD systems have lengthened the maximal transmission distance to 50 km over commercial fiber.[17]Very recently, a remote experiment CVQKD proposal has been proposed to extend the transmission distance to 202.81 km,which shortens the performance gap with the current point-to-point DVQKD systems.[18]

Except these methods above for extending the transmission distance of CVQKD, on the other hand, some local non-Gaussian operations are introduced to achieve this same purpose,[28–37]due to the fact non-Gaussian operations can be used to further distill the entanglement, such as photon addition (PA),[38–40]photon subtraction (PS),[38,39,41,42]quantum scissors,[43–45]and photon catalysis operations.[46–48]For example,the noiseless linear amplification(NLA)has been used to improve the maximal transmission distance roughly by the equivalent of 20log10gdB losses(gis the gain of the NLA)because of its compensation of the losses.[49,50]The PS-CVQKD protocol[29,36]has been proposed to improve its performances including secret key rate,maximal tolerable excess noise,and transmission distance. It is worth mentioning that the event of implementing non-Gaussian operations is probabilistic,especially for the success probability of the PS being less than 25%,which inevitably makes Alice and Bob lose more effective information. Recently,the performance of CVQKD is investigated when non-Gaussian operations are acted on both sides of the channels,[34]including PS,PA,and photon catalysis. It is shown that the PA operation performs the worst,although the PA presents higher success probability than the PS.However,the non-Gaussian operations are usually placed in mode B on the right-side of the entangled source. Here we propose another scheme for further improving the performance of CVQKD by operating PA operation in mode A on the left-side of the entangled source,under the entanglementbased(EB)version of CVQKD,denoted as the APA-CVQKD.It is shown that the PA operation on the left-side presents better secure key rate and transmission distance than the PS on the right-side,although both of them share the same maximal tolerable noise.Compared to both PS and PA on the right side,the proposed scheme shows the best performance. It is worth noting that the right(left)side of the entangled source means the mode from the entangled source to the quantum channel(from the entanglement source to the heterodyne detection at Alice’s port(see Fig.1)).

The rest of this paper is organized as follows. In Section 2,we first introduce the EB version of the APA-CVQKD and then achieve the relationship between input and output characteristic functions(CF)after general non-Gaussian operations,which is helpful to obtain the covariance matrix before the detections of both Alice and Bob.In Section 3,we give the performance analysis of the APA-CVQKD under the security against the collective attack. Finally,our main conclusions are drawn in Section 4.

2. The EB version of the APA-CVQKD

Figure 1(b) is our scheme,i.e., the EB version of the APA-CVQKD. Here the sender, Alice, first prepares an EPR entangled source (also called two-mode squeezed state) on modes A and B,keeping mode A for going through the singlephoton addition and the heterodyne detection on the left side of Fig.1(b),while sending the other mode B through an insecure quantum channel to the receiver,Bob,for performing the homodyne detection. After Alice and Bob share two correlated Gaussian variables,the secret key rate can be extracted by the post-processing including reconciliation and privacy amplification.

Fig. 1. (a) The schematic diagram of non-Gaussian operation. States |m〉 and |n〉 are, respectively, Fock state in auxiliary mode C |Ψ〉in: any input state;|Ψ〉out: output state after non-Gaussian operations;B(T): beam splitter with a transmittance T. (b)The schematic diagram of the PA-embedded CVQKD;Einstein–Podolsky–Rosen(EPR):two-mode squeezed vacuum state,LS:left-side,RS:right-side,Tc and ε: quantum channel parameters.

withb1=b2=cosh2r,b3=sinh2r.

In order to discuss the performance of APA-CVQKD,we need to achieve the covariance matrix before Alice and Bob’s detections. For this purpose, we first introduce the relation of CF between the input and output states after general non-Gaussian operations. As shown in Fig.1(a),non-Gaussian operations, including PS,PA,and photon catalysis, can be realized with an asymmetrical beam splitter and condition measurement of photon number detector. The case form ＞nmeans the PA, while the cases form ＜nandm=nare the PS and the quantum catalysis, respectively. In particular, for the case of single-photon as input and zero-photon detection,the single PA is achieved. In the following,we shall consider the single PA on Alice’s left-side,which is different from previous works that the non-Gaussian operations are often placed on Alice’s right-side.

For an arbitrary input stateρ,using the Weyl representation of density operators,i.e.,

whereχ(η)denotes the CF ofρandD(η)=exp(ηa†−η∗a)denotes the displacement operator, then the CF of the output state after undergoing the general non-Gaussian operation is shown as

In general,we assume that Eve is more powerful to control the quantum channel which is characteristic of transmittanceTcand excess noiseε.If Bob received the resulting stateρA1B1after going through the quantum channel,then the final CF of output state is given by

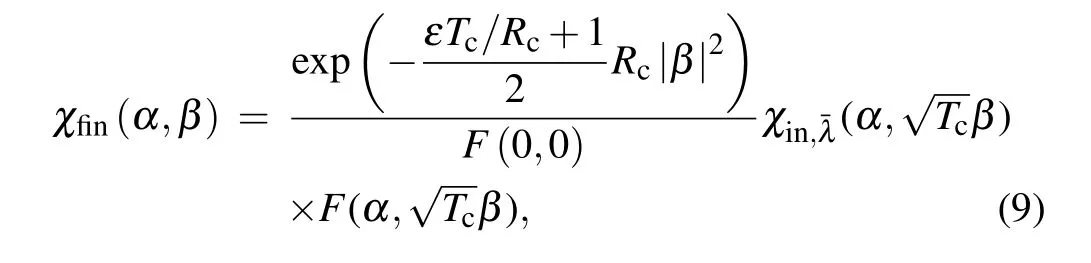
withRc=1−Tc. When the CF is known,we can derive some average values of operators consisting of two orthogonal components,such as

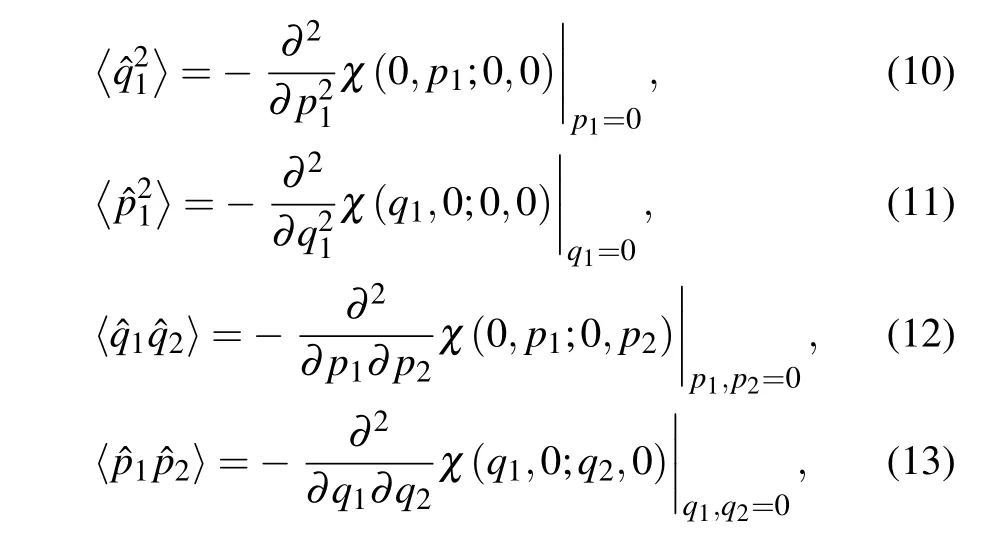
whereα=q1+ip1,β=q2+ip2.

Thus,using Eqs.(9)–(13),the covariance matrixΓof the final CF prior to the homodyne detection can be expressed as

Equation(14)is just the covariance matrix corresponding to the non-Gaussian states before Alice and Bob’s detections.However, for non-Gaussian states, it should be noticed that equation (14) cannot be directly used to calculate the secret key rate. It is fortunate that one can employ a lower bound on secret key rate to describe the secure performance based on a Gaussian state with the same covariance matrix shown in Eq. (14), whereKnon≥KG(KnonandKGare the secret key rates of the non-Gaussian and Gaussian states with the same covariance matrix,respectively).

3. Performance analysis of APA-CVQKD

In this section, we shall pay attention to the calculation of secret key rate for our scheme in the asymptotic limit,and provide the corresponding performance analysis.

3.1. Secure key rate

From the viewpoint of attack strategies executed by Eve,there exist three kinds of attacks: individual attack, collective attack,and coherent attack. For simplicity of calculations,here let us focus on the asymptotic secret key rate for reverse reconciliation under the collective attack which is the optimality of Gaussian attacks. According to the extremality theorem of Gaussian quantum states, the secret key rateKnonfor our scheme in the asymptotic limit can be written as

whereF(0,0)is the success probability for implementing the single-photon addition given in Eq. (7),βis the reconciliation efficiency,I(A:B) is the Shannon mutual information between Alice and Bob. It is noticed that Alice and Bob perform heterodyne and homodyne detections,respectively,thusI(A:B)can be derived using Eq.(14),i.e.,

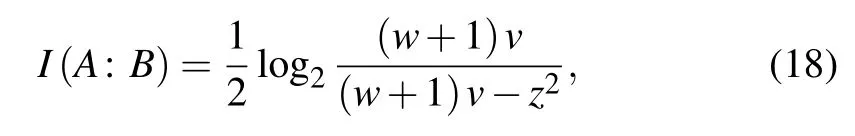
andS(B:E)is the Holevo bound which means the maximum information available to Eve on Bob’s key,i.e.,

Here we have assumed that Eve can purify the whole system so thatS(E)=S(AB) andS(E|B)=S(A|B),in whichS(AB) is a function of the symplectic eigenvaluesλ1,2ofΓandS(A|B) is a function of the symplectic eigenvalueλ3ofΓhom=wI −zσZ(vI+I)−1(zσZ)T,S(AB)andS(A|B)can be calculated as

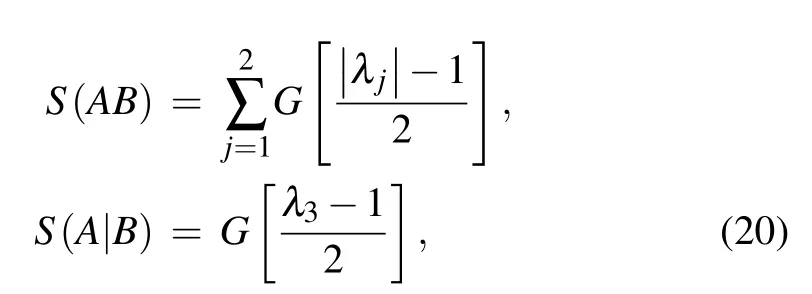
withG(x)=(x+1)log2(x+1)−xlog2xand

3.2. Performance analysis

After deriving the secret key rate in the asymptotic limit,in this subsection, we shall first compare the success probabilities for the PS and PA cases,and then mainly focus on the security analyses for our scheme in terms of the secret key rate,the transmission distances and the tolerable excess noises.

According to Eq.(17),one can see that the success probability is closely related to the secret key rate. Thus, we first compare the success probabilities between the PS and the PA as a function ofλandT,as illustrated in Fig.2. Distinctly,the success probability of implementing the PA is always higher than that of the PS,especially at the ranges of small squeezingλand low transmittanceT. This case makes it possible that the secret key rate with the PA-CVQKD can be higher than that with the PS-CVQKD.

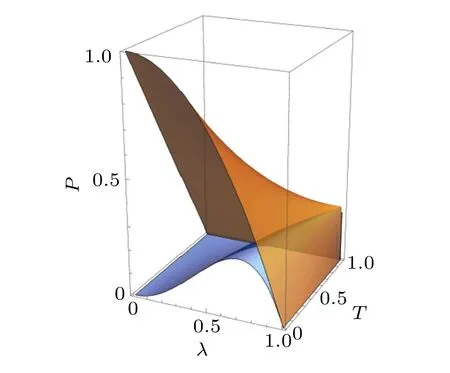
Fig. 2. The success probability as a function of squeezing parameter λ and transmittance T for single-photon subtraction and single-photon addition operations.

Actually, there are some non-Gaussian operations employed to improve the performance of EB-based CVQKD,such as the PA in mode A,the PA in mode B(denoted as BPACVQKD) and the PS in mode B (denoted as BPS-CVQKD).The latter two cases correspond to the case where the non-Gaussian operation is on the right side of the entangled source.Here we make a comparison about the performance of the secret key rate under these three schemes above. In Fig. 3, we show the secret key rate as a function of transmission distance and squeezing parameterλat given some parametersε=0.01,β=0.95,andλ=0.45,0.50,0.55,0.60,0.65,0.70,0.75, 0.80, 0.85, 0.90, 0.95, 0.999, when optimized over the transmittanceT. From Fig. 3, it is not difficult to see that the maximal transmission distance and the optimal secret key rate of both APA-CVQKD and BPS-CVQKD show a clear advantage over the BPA-CVQKD. In addition, our proposed APA-CVQKD scheme under the same accessible parameters presents higher secret key rates than the BPS-CVQKD.To further see these points, at fixed parametersε=0.01,β=0.95 andλ=0.95,we further compare the three schemes in terms of secret key rates changing with the transmission distance for optimal choices ofTin Fig.4(a),and the optimal values ofTcorresponding to the maximum secret key rates are shown in Fig.4(b).From Fig.4(a)it is shown that the secret key rate for the original CVQKD(black solid line)shows the best performance within a short distance.The reason is that the secret key rate for several non-Gaussian schemes may be restricted by its implementation probability at short-distance ranges. However,it can be surpassed by both our scheme(APA-CVQKD)and BPS-CVQKD at long-distance ranges, especially for our scheme because of the higher probability of the PA compared to the PS case (see Fig. 2). The corresponding optimalTis about 0.666≤T ≤0.670 for the long distance transmission, see Fig. 4(b). In addition, the PA operation in mode B is the worst one among these schemes including the original CVQKD. The main reason may be that the PA operation on right side introduces more noise.[34]

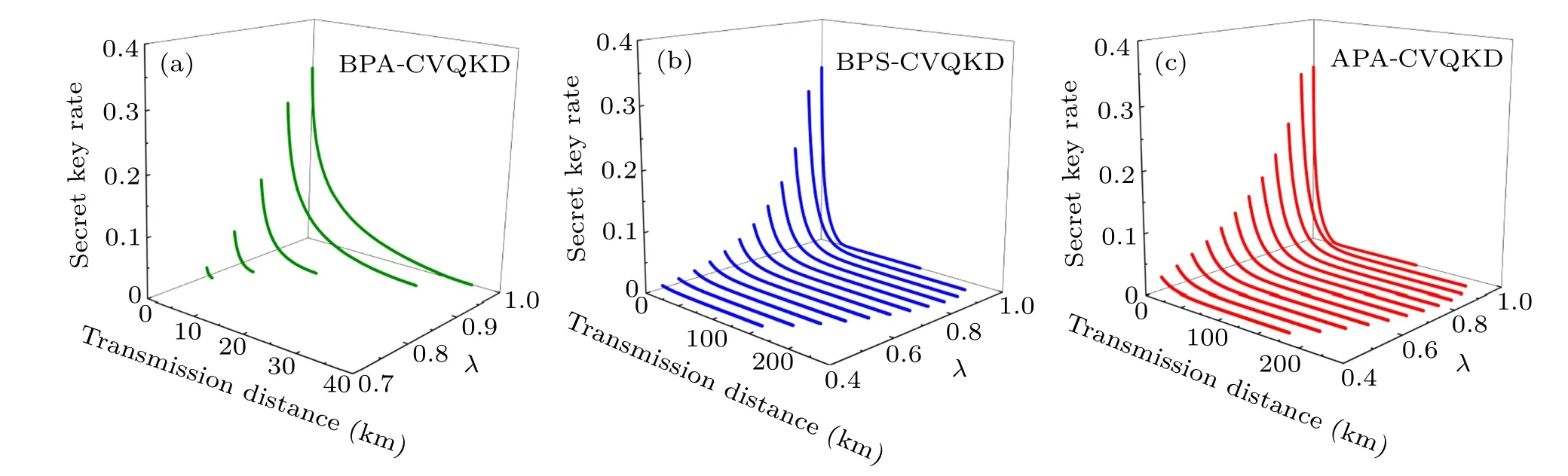
Fig.3. The secret key rate of(a)the BPA-CVQKD,(b)the BPS-CVQKD,and(c)the APA-CVQKD as a function of transmission distance and λ for given tolerable excess noise ε =0.01,β =0.95. λ =0.45,0.50,0.55,0.60,0.65,0.70,0.75,0.80,0.85,0.90,0.95,0.999.

Fig. 4. (a) The optimal secret key rates over transmittance T of the APA-CVQKD (red line), the BPA-CVQKD (green line), the BPS-CVQKD (blue line),and the original protocol(black line)as a function of transmission distance when ε =0.01,λ =0.95,β =0.95. (b)The optimal T changing with transmission distance for the maximal secret key rates in panel(a).

Next,we further consider the effects of different reconciliation efficienciesβand tolerable excess noisesεon the whole system performance. For several different values ofβandε,we plot the secret key rate as the function of the transmission distance in Fig. 5. For a comparison, both the BPS-CVQKD and the BPA-CVQKD cases are also shown here. From Fig.5,it is shown that the transmission distance of all these schemes increases with either the increase ofβor the decrease ofε,as expected. It is interesting that, for different excess noises(Fig.5(b))or reconciliation efficiencies(Fig.5(a)),the performance of our scheme is the best, allowing a longer transmission distance and a better secret key rate. While the performance of the BPA-CVQKD is still the worst.

On the other hand, the tolerable excess noise is often used as an important factor of evaluating the performance of the CVQKD.Figure 6 shows the tolerable excess noise of all the schemes as the function of the transmission distance at given parametersβ=0.95 andλ=0.95. It is worth mentioning that the two curves for both APA-CVQKD and BPSCVQKD schemes are exactly coincident, which implies that the success probability of non-Gaussian operations has no effect on the maximal tolerable excess noise corresponding to the condition ofKnon=0, but on the special case when the distance is given. In addition,it is interesting that our scheme at long distance range can present better stability in contrast of the original CVQKD and BPA-CVQKD schemes,because the curve for APA-CVQKD has a tiny change with the increase of transmission distance. For instance,for our scheme,the maximal tolerable excess noise can approach about 0.0183 over the transmission distance of 293 km,which implies that when the tolerable excess noise of quantum channel has a low valueε ∈(0,0.0183), the proposed scheme can satisfy the requirement of long-secure transmission distance with higher secret key rates.

Fig.5.The secret key rate of the APA-CVQKD,the BPA-CVQKD,the BPSCVQKD,and original protocol as a function of transmission distance when the transmittance T is optimized for given different values of (a) β =0.95(solid lines), β =0.90 (dash lines), β =0.85 (short-dot lines), λ =0.95 and ε =0.01; (b) ε =0.01 (solid lines), ε =0.02 (dash lines), ε =0.03(short-dot lines),λ =0.95 and β =0.95.

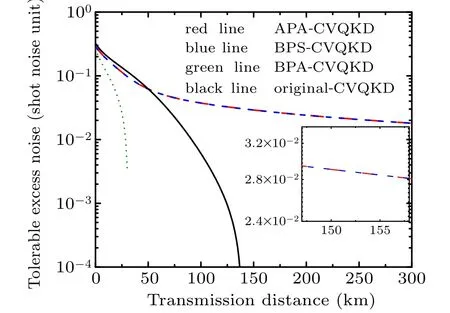
Fig.6. The tolerable excess noise of the APA-CVQKD(red line),the BPSCVQKD(blue line),the BPA-CVQKD(green line),and the original protocol(black line)as a function of transmission distance when T is optimized for given β =0.95 and λ =0.95.

4. Conclusions

In this paper, we have shown an improved performance of CVQKD with the photon-addition on the left-side of the entangled source under the EB scheme. Using the relation between the CF and the average values, we derived the covariance matrix between the legitimate communication parties prior to the corresponding detections. Then based on the Gaussian optimality theorem, we further discussed the lower bound of secret key rate for our scheme against the collective attack. It is found that the photon-addition operation on left side presents both higher success probability and better secure key rate and transmission distance than the photon subtraction on right side, although they share the same maximal tolerable noise. In addition, compared to both photon subtraction and photon addition on right side,our scheme shows the best performance and the photon addition on right side is the worst.