Floquet topological phase transition in two-dimensional quadratic band crossing system∗
Guo-Bao Zhu(朱国宝) and Hui-Min Yang(杨慧敏)
School of Physics and Electronic Engineering,Heze University,Heze 274015,China
Keywords: shaking,quadratic band crossing,orbital
1. Introduction
Topological phases and phase transitions have become the subject of tremendous interest over the last decade.[1–3]In twodimensional (2D) systems, topological insulating phases can be understood as generalizations of the quantum Hall effect.The quantum anomalous Hall effect[4]and the quantum spin Hall effect[5]have been predicted and intensively studied.[6,7]
On the other hand,ultracold atoms in optical lattices provide a clean and well-controllable platform to engineer the Hall effect.[8–15]For example,Goldmanet al.[8]have shown a remarkable anomalous quantum Hall effect with an ultracold Fermi gas loaded in an optical square lattice and subjected to an external and classical non-Abelian gauge field. Kennedyet al.[9]have proposed a scheme to realize the quantum spin Hall effect for neutral atoms in optical lattices. Fractional quantum Hall states of dipolar fermions have been studied in a strained optical lattice.[11]Liet al.[13]studied the tunable quantum Hall effects in a non-Abelian honeycomb optical lattice. Phucet al.[14]proposed a many-body spin Hall effect induced by the dipole–dipole interaction.
Moreover, time-periodic driving can be a powerful tool for manipulating quantum states in an optical lattice. In systems of ultracold atoms in optical lattices, Floquet modulation can be used to simulate anomalous quantum Hall phases and analog of topological insulators.[16]In a two-dimensional honeycomb lattice, the quantum anomalous Hall effect can be achieved by shaking optical lattices.[17,18]Meiet al.[19]have proposed the method to simulate and detect topological insulators with cold atoms trapped in a one-dimensional bichromatic optical lattice subjected to a time-periodic modulation. Furthermore, time-periodic modulations were used to study the topology properties of interacting fermionic atoms in shaken square optical lattices.[20,21]A periodic driving protocol was proposed to engineer large-Chern-number phases with the quantum anomalous Hall effect in a periodically shaken optical dice model.[22]
Given this background, we study quadratic band crossing (QBC) fermions in a square optical lattice, which have attracted intensive studies in modern condensed matter physics.[23–28]We find that the interplay between the shaking,orbital Zeeman term, and the spin–orbit coupling can lead to the nontrivial topology characterized by the(spin)Chern number of its energy band. By varying the orbital Zeeman term and shaking strength,the quantum spin Hall(QSH)and quantum anomalous Hall (QAH) phase may appear. Our findings would provide a way to study the topological physics of QBC fermions.
This paper is organized as follows. We first present the model Hamiltonian, including the scheme of shaking, orbital Zeeman term,and the spin–orbit coupling in Section 2.In Section 3,we analyze band structures. Based on these results,we further obtain the phase diagram of Hall phases in Section 4.Finally,in Section 5,we give a brief conclusion.
2. Model and method
We use the following low-energy effective Hamiltonian to describe QBC fermions in a square optical lattice

where
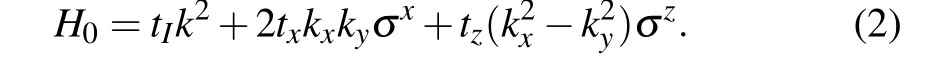
HeretI,x,zare determined by the hopping between orbitals on neighboring sites in a square optical lattice,andσx,y,zare corresponding Pauli matrices in thepxy-orbital space[29](see appendix A for details). The second part is the spin–orbit coupling(SOC),which is modeled as[30–32]

whereλis the spin–orbit coupling(SOC)strength,ands=±are the spin index for the spin up and down bands. In optical lattice, SOC is experimentally realized via the Raman technique.[33–36]The last term is orbital Zeeman term from the on-site rotation by rotating each optical lattice site around its own center,[37]and is described by[38,39]

The last two terms break the time-reversal symmetry and induce topologically nontrivial band structures.txis taken as the unit of the parameters.
For a shaken optical lattice, the vector potential coming from shaking has the form[21]

whereA0=ωs0kL/ERis the dimensionless shaking strength,andkLandERare recoil momentum and recoil energy, respectively. In the practical experiment,weak lattice shaking is preferred to make induced heating on the lattice small. Then the above time-dependent Hamiltonian can be captured by an effective time-independent Hamiltonian as[19,40,41]

andη=±1 denote the circularity of shaking, which correspond to theϑ=∓π/2, respectively. Based on the above equations, we can obtain that the shaking induced SOC-like term is introduced, and its sign depends on the circularity of shaking.
3. Band structure
Diagonalizing Eq.(6),we obtain the energy dispersion
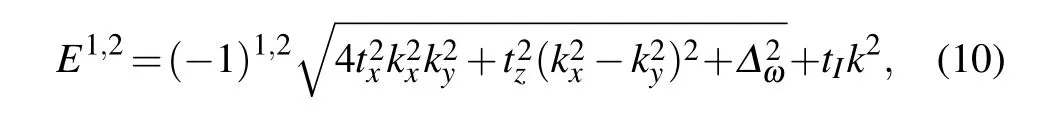
where∆ω=sλ −V −Vωη. The parameterstI,x,zcan be controlled by the over-lap between orbital on neighboring sites. It should be noted that the termtIk2does not modify the eigenstates and topological properties of the system. Therefore,we consider the system withtI=0.
Figures 1 and 2 show the evolution of the energy band near QBC point along with the increase of a shaking strength at circularity of shakingη=−1 andtx=tzatλ= 0.05tx,V=0.1txandλ=0.05tx,V=0.01tx,respectively. When the shaking is present,a bulk gap is opened due to SOC andV,and the four bands are nondegenerate. Forλ <V,the band gap of spin-up(s=1)bands firstly closes and then reopens with the increase of a shaking strength. With the further increase of a shaking strength, the band gap of spin-down (s=−1) bands closes and then reopens. Forλ >V, the band gap of spindown bands closes and reopens, while the band gap of spinup bands always increases. This band structure is drastically modified by shaking;the rich change of band gaps in the system is shown in Fig. 3 under the interplay between SOC,V,and shaking. Moreover,the presence of such a bulk gap indicates an insulating state. The quantum Hall effect can be engineered by opening a gap at a topological Fermi point with a quadratic band dispersion.As a consequence,the band topologies may get changed with the evolution of the band gap,and interesting topological transitions occur. As we argue below,this insulating state is topologically nontrivial and exhibiting a quantized Hall conductance.
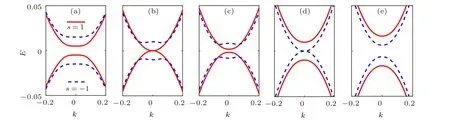
Fig.1. Band structures near quadratic band crossing(QBC)point under the circularity of shaking η =−1 at λ =0.05tx,V =0.1tx,and tI =0 for a shaking strength A0 of (a) 0, (b) 0.278, (c) 0.3, (d) 0.365, (e) 0.4, respectively. The solid red and dashed blue lines denote spin-up (s=1) and spin-down(s=−1)bands,respectively.

Fig. 2. Band structures near QBC point under the circularity of shaking η =−1 at λ =0.05tx,V =0.01tx, and tI =0 for a shaking strength A0 of(a)0, (b)0.291, (c)0.35, respectively. The solid red and dashed blue lines denote spin-up(s=1)and spin-down(s=−1)bands,respectively.

Fig.3. Band gap(2|∆ω|k=0)as a function of the shaking strength A0 for(a)η=−1,λ <V,(b)η=−1,λ >V,(c)η=1,λ <V,and(d)η=1,λ >V.The solid red and dashed blue lines denote spin-up (s=1) and spin-down(s=−1)bands,respectively.
4. Phase diagram
For two dimensional system,the Hamiltonian can be expressed in terms of the Pauli matrices as
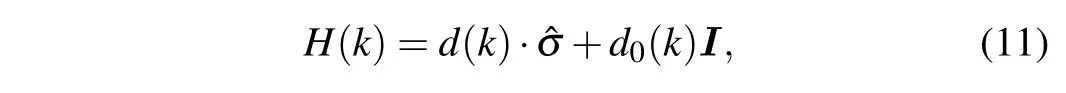
whered(k)=(dx(k),dy(k),dz(k)),=(σx,σy,σz), andIis 2×2 identity matrix. Then,due to the good quantum numbers of spin,the corresponding Chern number for spinscomponent is calculated as[42]

whereΩsis the Berry curvature of spinscomponent in the momentum space over all occupied states,and it can be written as
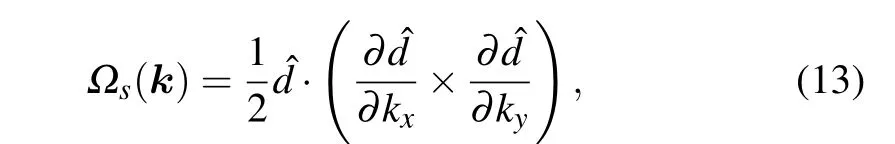
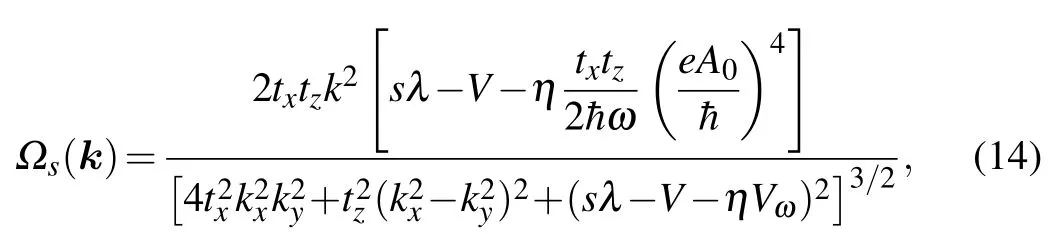

where sgn is the sign function.

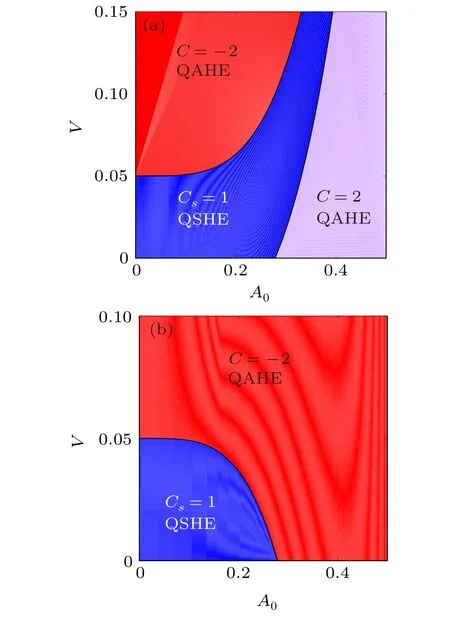
Fig.4. Phase diagram in the(A0,V)plane at fixed λ =0.05 for circularity of shaking(a)η=−1 and(b)η=1. There are two QAH phases,which are identical Chern number C=2 and C=−2,respectively. The other phase is QSH phase with spin Chern number Cs=1.
In addition to Chern number and spin Chern number,we discuss the energy gaps,which provide a more intuitive picture to characterize the topological phase transition. A topological phase transition occurs when the energy gap closes and reopens. In Fig.3,we plot the band gap evolution as a function of shaking strengthA0. Forλ <V,we find that the band gaps always open forη=1,while the process of band gap closing and reopening occurs twice forη=−1.It means that there are two or no topological phase transitions along with the increase of shaking strength depending on the circularity of shaking.Forλ >V, one can observe that the band gap of spin-up or spin-down bands opens and reopens,which is independent of the circularity of shaking. It indicates that a topological phase transition occurs.
The appearance of the edge state is another hallmark QAHE state. As an example, Fig. 5 shows the band structure of a ribbon under the shakingη=−1 atλ= 0.05tx,V=0.01tx, andtI=0 for open boundary condition in thexdirection without(a)and with(b)the shaking driving. When the shaking driving is absent,the edge state does not exist for a given Fermi level(EF=0).While there are four different edge states when the shaking driving is included. The emergence of edge states in the gap is intimately related to the topological property of the Bloch states in the valence bands. The numbers of edge states are in agreement with the Chern number.
Moreover, many techniques have been implemented to detect QAH and QSH states in the optical lattice in the experiment. Chiral edge states and topological order are hallmarks of quantum Hall physics. Albaet al.[43]provided the time-of-flight imaging methodology through measuring atomic distribution in momentum space.By performing Bloch oscillations,[40,44]an experimental value for the Chern number has been obtained. Using atomic interferometry in real and momentum space,[45–47]topological invariants of topological band structures in the optical lattice can be measured. By imaging individual sites along a synthetic dimension, Goldmanet al.[48]have reported on the experimental realization of chiral edge states, which are hallmarks of quantum Hall physics.
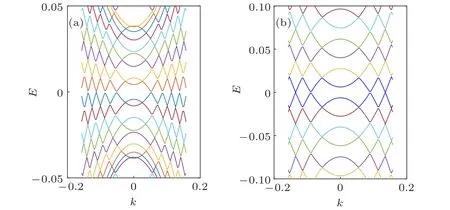
Fig.5. Band structure of a ribbon under the shaking η =−1 at λ =0.05tx,V =0.01tx,and tI =0 before and after closing the gap with a shaking strength of(a)0.2 and(b)0.4,respectively.
5. Conclusion
We have studied the Hall effects of quadratic band crossing(QBC)fermions in a square optical lattice with spin–orbit coupling and orbital Zeeman term. By analyzing the energy gap and (spin) Chern numbers, we find that the orbital Zeeman term or shaking can drive a topological transition from spin Hall phases to anomalous Hall phase.The orbital Zeeman term can interplay with spin–orbit coupling and the shaking,and leads to rich phases.Our results provide a way to study the topological physics of spin–orbit coupling or shaking-driven topological phase.
Appendix A:Effective Hamiltonian
We consider ultracold fermionic atoms trapped in a square optical lattice with orbitals(px,py,andd). We assume that all the atoms are trapped in the lowest band of the optical lattice. Using perturbation theory,[29,49]one can get the tight-binding Hamiltonian in momentum space on the basis of{px(k),py(k)}
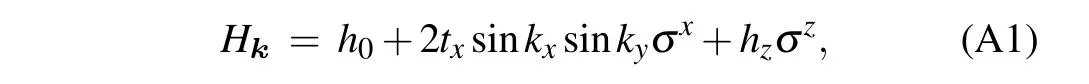
whereh0=tppcoskx −t'ppcosky+tppcosky −t'ppcoskx+txsin2kx+txsin2ky,hz=tppcoskx −t'ppcosky −tppcosky+t'ppcoskx+txsin2kx −txsin2ky, andtx=2t2pd/(2tpp −2t'pp+4tdd −δ).tpp,t'pp,tdd,tpdare the hopping amplitudes between orbitals on neighboring sites, andδdescribes the energy difference betweenpanddorbitals. To describe QBC fermions,we expand the momentum around theΓpoint and obtain
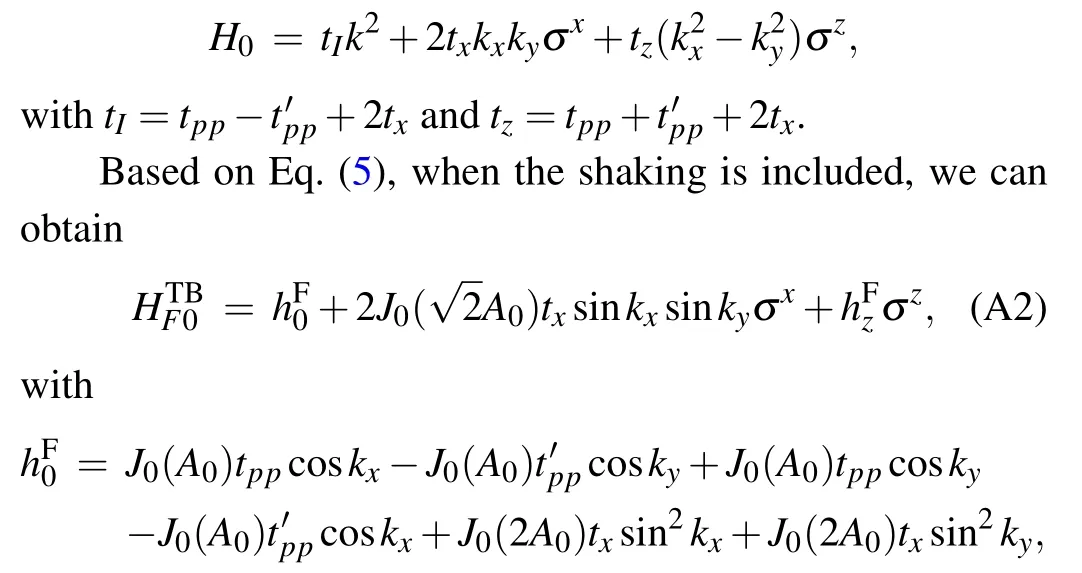

——钟表也要萌萌哒
- Chinese Physics B的其它文章
- Quantum computation and simulation with vibrational modes of trapped ions
- ℋ∞state estimation for Markov jump neural networks with transition probabilities subject to the persistent dwell-time switching rule∗
- Effect of symmetrical frequency chirp on pair production∗
- Entanglement properties of GHZ and W superposition state and its decayed states∗
- Lie transformation on shortcut to adiabaticity in parametric driving quantum systems∗
- Controlled quantum teleportation of an unknown single-qutrit state in noisy channels with memory∗

