低秩张量填充的随机算法

郭雄伟，王川龙

（太原师范学院 数学系，山西 晋中030619）

0 引言

张量填充（TC）问题是张量研究中最活跃的热点之一.张量填充可以应用于很多领域，如图像恢复［1，2］、数据挖掘［3］、信号处理、机器学习［4］、高阶网络链接分析［5］等.张量填充问题可以表述为如下形式：

其中A，Γ都是n-模张量，且每个模的大小相同，rank（A）表示张量A的某种秩，PΩ是集合Ω上的正交投影，Ω是基数为m的随机子集，其中m是采样元素的个数.当（i1，i2，…，in）∈Ω时，PΩ（A）的第（i1，i2，…，in）个元素等于Γi1i2…in，否则等于0.张量的秩的计算是NP-难问题.因此，一些学者将模型（1）松弛为如下凸优化模型：

其中αi≥0且张量填充问题可以看作是矩阵填充问题的高维形式.

在张量填充的优化算法方面，已有一些研究成果.文献［6］中Liu等人给出了张量的核范数的定义，并基于模型（2）提出了三种有效算法：简单低秩张量填充算法（Simple Low Rank Tensor Completion algorithm，SiLRTC）、快速低秩张量填充算法（Fast Low Rank Tensor Completion algorithm，FaLRTC）以及高精度低秩张量填充算法（High accuracy Low Rank Tensor Completion algorithm，HaLRTC）.在文献［7］中，Gandy等人用张量的秩作为稀疏表示，将其模型转换为更容易求解的凸模型，提出了张量恢复的Douglas-Rachford算法（Douglas-Rachford splitting algorithm for Tensor Recovery）以及交替方向乘子法（Alternating direction method of multipliers）.受矩阵填充算法的启发，Tan等人［8］将张量填充问题矩阵化为n个矩阵填充问题，提出了低多线性秩张量填充（Low Multilinear Rank Tensor Completion，LMRTC）算法.为了保持张量原有的内部结构以及避免矩阵化的计算花费，Kilmer等人［9］提出了张量的奇异值分解，且能够很好地保留张量原有的内部结构信息.基于张量的奇异值分解和管秩的定义，Zhang等人［10］利用交替方向乘子法框架，给出了相应的算法.此外，还有很多学者研究张量的CP秩以及基于CP秩的张量填充算法，详见文献［11-13］.

本文主要研究张量填充问题.基于Liu等人［6］提出的高精度低秩张量填充算法，引入随机的思想，并给出相应的算法，同时通过数值实验和图像填充验证算法的有效性.

本文的结构安排如下：第1节介绍张量及矩阵的相关符号说明和定义；第2节回顾高精度低秩张量填充算法，在此算法的基础上引入随机的思想，给出随机高精度低秩张量填充算法的具体步骤；第3节通过数值实验以及图像填充与HaLRTC及DR-TR算法比较，验证算法的有效性；第4节对全文进行总结.

1 符号说明及定义

为方便起见，RI1×I2表示I1×I2的实矩阵全体.矩阵的核范数和F-范数分别表示为‖X‖＊和‖X‖F.矩阵的内积表示为表示n-模张量，它的元素表示为，其中表示张量的模-k展开.与其相反的运算定义为表示张量Χ的秩.用表示张量的F-范数.

定义1（奇异值分解（SVD））［14］秩r的矩阵，则必存在正交矩阵满足：

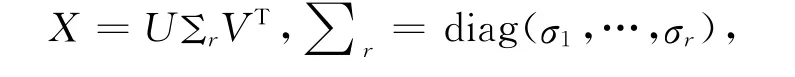
其中σ1≥σ2≥…≥σr≥0.

定义2（奇异值阈值算子）［15］对于任意参数τ≥0，奇异值阈值算子Dτ定义为：

2 算法

文献［6］基于模型（2），并结合交替方向乘子法（ADMM）框架，给出了高精度低秩张量填充算法.该算法具有较好的填充效果，其算法如下：

算法1 高精度低秩张量填充算法（High accuracy Low Rank Tensor Completion algorithm，简称HaLRTC）［6］

给定采样集合Ω，采样矩阵PΩ（Γ），参数αi，ρ0，t，ε，以及初始张量0，k：=0；

第1步：计算

第3步：若‖Χk+1-Χk‖F／‖Χk‖F＜ε，停止迭代；否则转第4步.

由算法1可知，在每次迭代过程中，该算法需要计算n次奇异值分解，张量展开以及矩阵折叠，需要较大的计算花费.在此算法的基础上，我们引入随机的思想，即在每次迭代过程中，只对随机产生的一个模进行奇异值分解，张量展开以及矩阵折叠，减少了计算花费.其算法如下：

算法2 低秩张量填充的随机算法（Low Rank Tensor Completion Random algorithm，简称LRTCR）

给定采样集合Ω，采样矩阵PΩ（Γ），参数αi，ρ0，t，ε，以及初始张量0，k：=0；

第1步：令

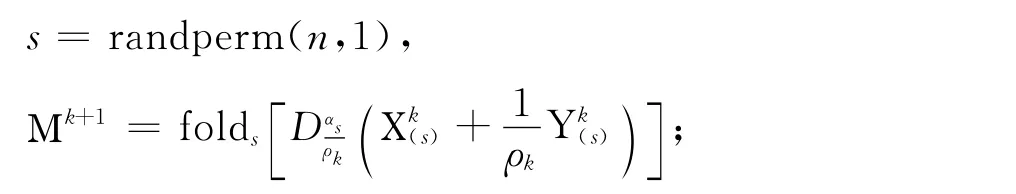
第3步：若‖Χk+1-Χk‖F／‖Χk‖F＜ε，停止迭代；否则转第4步；

3 数值实验

本节通过随机张量填充和图像填充将新算法与HaLRTC以及DR-TR算法比较.

3.1 随机张量填充

在本小节中，利用随机生成的维数为50×50×50，50×60×70的秩分别为（2，2，2）和（5，5，5）的三维张量，在采样率为0.2，0.3，0.4的情况下，比较其实验结果，实验结果见表1、表2、表3.Χ＊表示这三种算法的输出张量，Γ为原始张量.

表1 p=0.2时，算法LRTCR与算法HaLRTC、DR-TR比较

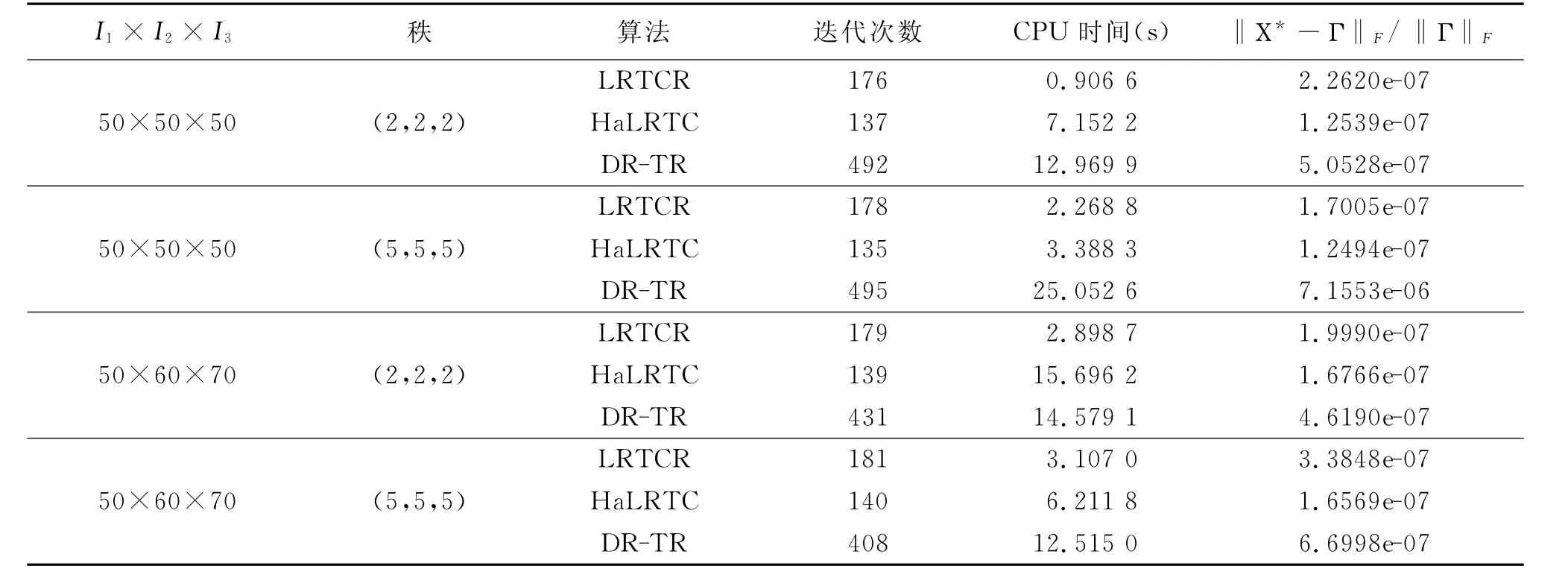
表2 p=0.3时，算法LRTCR与算法HaLRTC、DR-TR比较

表3 p=0.4时，算法LRTCR与算法HaLRTC、DR-TR比较

3.2 图像填充

在本小节中，使用维数为181×217×181的立体MRI①http：／／brainweb.bic.mni.mcgill.ca／brainweb／selection normal.html.数据比较新算法与HaLRTC及DR-TR算法的填充效果.随机选取MRI数据中的某一切片，在采样率分别为0.2，0.3，0.4的情况下，其填充效果见图1.为了直观展现其填充效率，表4中展示填充时间、迭代次数以及相对误差.

图1 填充效果图

表4 MRI在不同采样率下，算法LRTCR、HaLRTC、DR-TR比较

续表4

4 总结

本文提出了一种新的高精度低秩张量填充随机算法，简称LRTCR.该算法在原有的算法的基础上，引入随机的思想，有效地降低了算法在每次迭代过程中的计算花费.由表1-3可以看出，新算法与原有的算法相比，精度上大致相同，但新算法在时间花费上占有很大优势.此外，由图1及表4可以看出，针对MRI图像填充，新算法同样占有优势.