多自由度固有振动广义特征值问题的复分析证明1)
——工科教育中的理论思维能力培养一例
王怀磊
(南京航空航天大学振动工程研究所,南京210016)
(南京航空航天大学机械结构力学及控制国家重点实验室,南京210016)
线性N自由度无阻尼振动系统的运动微分方程(组)为

其中u为N自由度位移向量,K为系统刚度矩阵,M为系统质量矩阵。在求解该方程的固有振动时,可首先假设其具有同频率、同相位但不同振幅的固有振动形式解

其中ω和θ为待求实标量参数,在力学体系中分别代表固有频率和初相位,φ为待求非零N维实向量,代表固有振型。将式(2)代入式(1),得到这一运动形式存在的必要条件为:存在非零实向量φ,满足

或记作
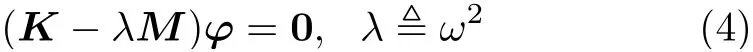
按照线性代数理论,方程(4)属于矩阵束K和M的广义特征值问题,其中标量λ和对应的非零向量φ分别称为广义特征值和广义特征向量。显然,方程(4)具有非零向量解的充要条件为
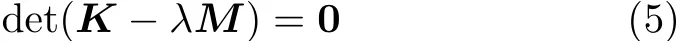
这是一个关于λ的一元N次代数方程,称为方程(1)的特征方程。求解矩阵广义特征值问题(4)就是先由特征方程(5)解出特征根λr,r=1,2,···,N,然后逐一代回式(3),寻求齐次线性代数方程的非零向量解φr,r=1,2,···,N的过程。
由于式(2)所假设的形式解代表实际的物理振动,因此其中各项参数都必须为实数,这就要求方程(4)必须有非负实特征值λ=ω2和对应的实特征向量φ。换句话说,如果要说明系统(1)存在如式(2)所示的固有振动形式解,必须要首先证明矩阵广义特征值问题(4)存在非负的实特征值λ。否则,如果尚不清楚非负实特征值和实特征向量是否存在就对式(4)进行左乘φT的操作,并进一步根据质量矩阵的正定性及刚度矩阵的半正定性判定出λ为非负实数,就会陷入逻辑上的循环论证,有可能导致错误的结论。因此,是否能证明矩阵广义特征值问题(4)的确具有非负实特征值,将对判断固有振动形式解(2)的存在性起到关键的作用。
由于质量矩阵M一般为正定矩阵,刚度矩阵K一般为半正定矩阵,所以大多数振动力学或结构动力学的教材[1-4]在论证上述结论时,都是利用质量矩阵M的Cholesky分解(平方根分解)将式(4)的矩阵广义特征值问题转化为与其具有完全相同特征值的标准特征值问题,再利用标准特征值的经典理论判断出广义特征值问题的所有特征值都是实数;而另外还有一些教材则主要专注于介绍力学概念而跳过相关的数学证明[5]。笔者在振动理论课的教学实践过程中发现,对于仅学习过线性代数而尚未学习矩阵论课程的本科阶段学生而言,理解基于矩阵的Cholesky分解的证明具有一定的困难,绝大多数学生都只能采取暂时认同而不深究的态度,降低了他们对该结论的理性认知。为了在工科教育中使学生加强逻辑思维能力的训练及培养严谨的思维习惯,增强对振动理论的全面系统理解而又不带来使用超前理论工具的困难,笔者思考对该问题给出如下一个较为初等的复分析证明。
1 广义特征值问题的复分析证明
定理1.矩阵广义特征值问题(4)的特征值皆为非负实数。
证明:假设矩阵广义特征值问题(4)的任一特征值为一复数λ=λR+iλI,其中λR,λI为实数,i为纯虚数单位,其对应的复特征向量为φ=φR+iφI,φR和φI分别为特征向量的实部和虚部。将其代入方程(4)并化简得

令式(6)中的实部和虚部分别为零得

将式(7)的上式左乘,下式左乘得

由于质量阵和刚度阵都是对称矩阵,因此有

从而将式(8)中的两式相减即得
由于M为正定矩阵,因此0,又由于φR,φI不同时为零向量,从而必有,因此由式(10)可得

这就证明了矩阵广义特征值问题(4)的任一特征值λr必为实数,r=1,2,···,N。显然,其对应的特征向量φr也可取实数。利用实特征向量φr进一步定义系统的第r阶广义质量和第r阶广义刚度,并根据质量矩阵的正定性及刚度矩阵的半正定性可得

于是,对式(4)两端左乘实向量φT可解得

此即证明了矩阵广义特征值问题(4)的任一特征值必为非负实数,从而可以进一步求出系统的固有频率证毕。
上述定理的证明过程事实上已经求出了式(2)所设形式解中的所有未知量,也即说明了这种形式解的假设是合理的,它恰好反映了系统的固有振动形态。
值得指出的是,本文给出的复分析证明方法仅能说明广义特征值问题(4)的特征值皆为实数,从而可求出相应的实特征向量,但却无法利用其证明系统具有N个线性无关的实特征向量。这一结论的证明仍须利用Cholesky分解将广义特征值问题转化为标准特征值问题,得到二者之间的一一对应关系,再利用标准特征值问题的基本结论得出广义特征值问题也具有N个线性无关的特征向量,其物理意义即为N自由度线性振动系统具有N个独立的模态振型。
2 结论
多自由度振动系统固有振动的求解最后归结为质量阵和刚度阵的矩阵广义特征值问题,而固有振动形式解的存在性要求该矩阵广义特征值问题具有实的特征值和特征向量。现有振动理论教材在讨论线性系统的固有振动时,有的为强调物理概念而直接默认该广义特征值问题具有实特征值,有的则给出基于矩阵分解理论的矩阵分析证明。本文给出的这种复分析证明仅使用复数的基本概念和简单的矩阵代数运算,而不涉及矩阵分解理论,在降低数学论证难度的同时又保持了分析的严密性,这对尚未学习矩阵论课程的本科阶段的学生而言,不仅易于加深他们对结论的理解,而且将有助于他们在工科课程的学习过程中培养或保持严谨的理论思维习惯。需要指出的是,该方法并不能完全替代矩阵分解理论给出的证明,若要进一步证明广义特征值问题具有N个线性无关的特征向量,即线性振动系统具有N个独立的模态振型,仍须利用矩阵分解理论加以论证。

