时间分割圆弧插补算法的改进

梁晓兵，刘志强，王璠

（河南机电职业学院，郑州 451191）

0 引言

目前数控系统在插补圆弧的过程中，使用的基本上都是二阶近似法进行圆弧插补的，这种方法使用一组直线来逼近圆弧，计算出插补周期的坐标增量值。目前国内外很多学者已经在这方面进行了很多研究，韩赛飞等[1]实现了改进型圆弧插补算法及FPGA实现；刘焕等[2]分析了基于微分模型的空间圆弧与椭圆弧插补算法；姚晓通等[3]分析了圆弧插补算法的FPGA实现；李伟光等[4]分析了无限直线逼近圆弧方法；刘鹏飞等[5]分析了在机器人领域中的应用；何均等[6]实现了短线段空间圆弧转接与插补；刘放等[7]介绍了基于四元数的空间圆弧插补算法；王中平等[8]基于矢量分析了圆弧插补算法；詹泳等[9]实现了五轴空间圆弧插补；朱国力等[10]介绍了插补算法的应用；贺德华等[11]推导了空间任意圆弧的插补算法；高宏卿等[12]推导了空间圆弧变换插补原理与算法。

在计算过程中，传统插补算法使用了三角函数的泰勒展开式中的低阶近似，使得插补点远离圆弧，产生一定的累积误差。针对这种情况，提出一种改进的圆弧插补算法，进一步提高插补运算精度。

1时间分割法插补原理

现以第一象限逆时针插补为例，说明传统时间分割法实现原理。如图1所示，设待插补圆弧半径为R，圆心坐标（0，0），插补速度为F，插补周期为T，每次插补的进给步长f=F·T。

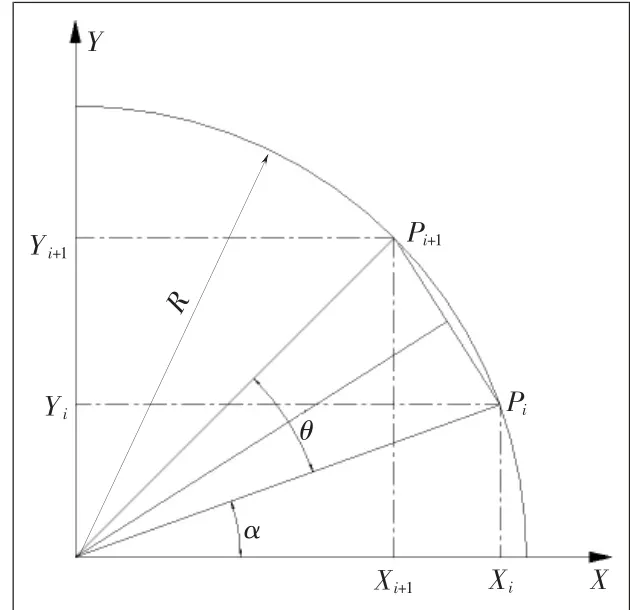
图1 圆弧逆时针插补两点位置关系

对圆弧上动点Pi（xi，yi），满足以下关系：

yi＝R·sinα；xi＝R·cosα。

Pi＋1（xi＋1，yi＋1）是下一插补点坐标，PiPi＋1是每插补周期的进给步长f，其对应的圆心角是θ。

下一插补点坐标值计算方法为

yi＋1＝R·sin（α＋θ）；xi＋1＝R·cos（α＋θ）。

展开后得：

对其中的三角函数泰勒展开并取二阶以下变量公式可得：

cosθ≈1－θ2/2；sinθ≈θ。

且由θ＝f/R，代入式（1）、式（2），可得：

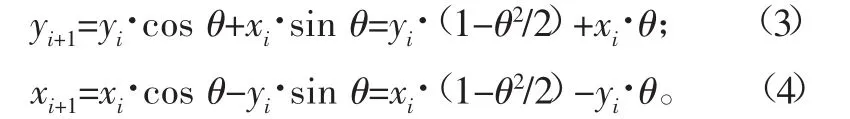
设A＝f/R＝θ，B＝θ2/2，代入式（3）、式（4），可得：

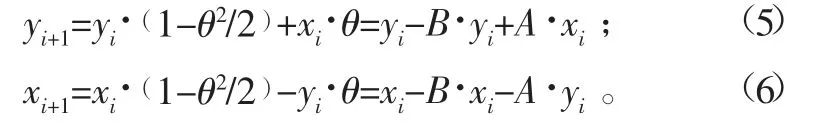
取Δyi＝yi＋1－yi＝－B·yi＋A·xi；Δxi＝xi＋1－xi＝－B·xi－A·yi。

弓高误差δ计算公式为

2 时间分割法改进算法

上面传统的时间分割法圆弧插补运算，引入了近似计算，存在一定的误差，而且弓高误差较大，为了减小误差，下面提出一种改进的时间分割圆弧插补改进方法。

2.1 改进算法原理

对于有一定误差的待加工面（如图2），如果实际加工面位于理论待加工面单侧，那么最大误差就是实际加工最大尺寸减去理论加工面尺寸。如果实际加工面位于理论待加工面两侧，那么，最大误差就是理论面和实际面两侧尺寸差的最大值，如果两面对称，最大误差就是实际误差的一半。

图2 待加工面

2.2 算法实现

对于给定的弓高误差δ和圆弧半径R，分别做半径为R-δ/2、R+δ/2圆弧，已知Pi（xi，yi）点，求下一插补点Pi+1（xi+1，yi+1）坐标。过Pi点做内圆弧的切线交半径为R-δ/2内圆弧于切点P（xq，yq）点，如图3所示。

图3 改进算法逆时针插补点位置关系

由于P点是切点，PPi是内圆弧切线，且PPi长度值为f/2，由几何关系可得：

代入式（10）、式（11），可以求得P（xq，yq）坐标为：

根据图3几何关系，P（xq，yq）为Pi（xi，yi）点和Pi+1（xi+1，yi+1）连线的中点，可知：

联立式（12）～式（15），可得：

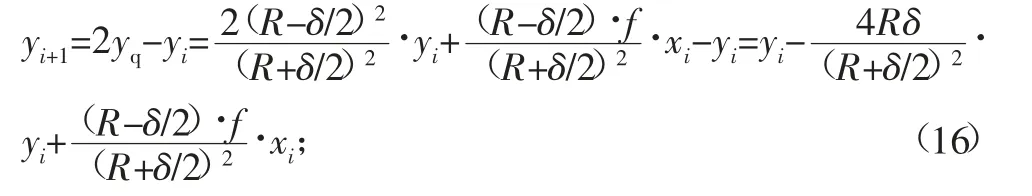
Δyi=yi+1-yi，Δxi=xi+1-xi，改进后的时间分割圆弧插补算法的计算步骤如下。

2.3 特殊点处理

由于上面为了减小误差，改进了算法，计算过程中插补的点都在半径为R+δ/2圆弧上，由此引入了2个特殊点即起点P0（x0，y0）和终点Pe（xe，ye），这两个特殊点需要特殊处理。

对于起点P0（x0，y0），给定的起点坐标位于半径为R的圆弧上，实际插补计算的起点位于半径为R+δ/2的圆弧上，因此需要计算插补起点Pc0（xc0，yc0）。

根据图3几何关系得：

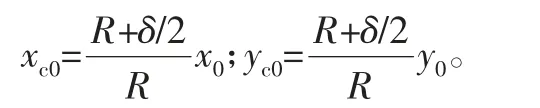
对于终点坐标Pe（xe，ye），实际需要的终点坐标位于半径为R圆弧上，实时插补计算的终点位于半径为R+δ/2圆弧上，因此需要计算实际终点Pea（xea，yea）。根据图3的几何关系可得：

3 两种算法比较分析

在传统算法中，由于对正弦余弦三角函数进行了二阶近似，由式（5）、式（6）求得的下一插补点可能会偏离圆弧产生径向误差。插补过程中由于使用了弦线代替圆弧，还会产生弓高误差。

在改进算法中，由于使用R+δ/2的圆弧代替半径为R的圆弧，同样会产生径向误差和弓高误差。

3.1 径向误差

径向误差即实际插补点坐标与理论坐标点的偏差，实际计算根据实际插补点坐标的坐标值与理论半径的距离来表示：

由式（5）、式（6）可得传统插补算法径向误差为

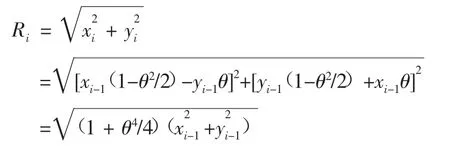
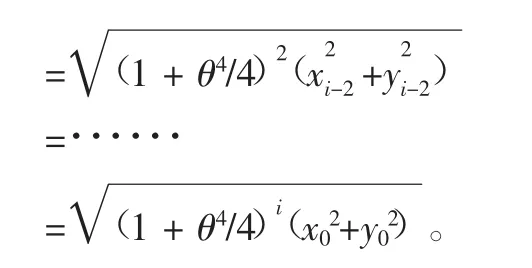
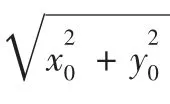
由于θ不为0，δci也不等于0，即存在径向误差，而且随着插补次数的增加，径向误差也会越来越大。

对于改进后的算法，由图3几何关系得

由式（16）、式（17）、式（19）得

代入式（18），可得

经过改进后，算法误差是恒定值，和插补次数无关，误差不累计，可以在预插补阶段进行误差补偿一个恒定值，进一步减小误差。

3.2 弓高误差

3.3 插补速度

在传统得插补算法中，使用了二阶近似来简化计算过程，改进算法没有采用近似处理，一方面是因为现在嵌入式系统计算能力越来越强，比如STM32等微控制器都带了硬件除法器；另一方面是因为本改进算法在插补过程中和传统插补算法过程一样，除了常量系数计算不一样，常量系数计算过程可以放到插补预处理阶段进行，而且改进算法比传统算法只多了一步除法运算。在168 MHz的STM32f407芯片上进行插补系数计算仿真，结果测得传统算法每次实际计算时间为0.148μs，改进后插补时间为0.369μs，时间基本一致。

综上，传统算法径向误差随插补次数的增加不断增加，改进算法后，径向误差不随插补次数变化而变化，稳定无变化。弓高误差传统算法为f2/(8R)，改进后算法误差为f2/(16R)，只是传统算法误差的一半。由于径向误差和弓高误差在相反方向，最大误差为径向误差和弓高误差的最大值。改进后算法最大误差为f2/(16R)，只是传统算法误差的一半。

4 结语

通过对时间分割圆弧插补算法和改进后的算法对比计算分析，可知改进算法的误差要比原来的算法误差减小一半，精度得到了很大提高。改进后插补过程运算速度相同，插补系数计算相对低一些，但是误差不到1μs，满足实时插补要求。