非线性薛定谔方程的几种差分格式

孙传志， 汪佳玲

(南京信息工程大学 数学与统计学院， 江苏 南京 210044)

1926年，物理学家薛定谔提出薛定谔方程，作为量子力学领域的基本方程，它对物理领域的研究具有深远意义.随着社会的发展进步，单纯线性模型已经不足以描述这个世界的所有现象，学者们将视线逐渐转移到非线性模型的研究.20世纪70年代，在含非线性项的色散方程的研究中，Hasegawa推导出非线性薛定谔(nonlinear Schrödinger equation，NLS)方程，广泛应用于应用数学和量子力学等物理领域，如光脉冲在色散与非线性介质中的传输，原子激光产生的Bose-Einstein凝聚效应，电磁场中超导电子的运动等.

NLS方程的一般形式为iut+uxx+β|u|2u=0.其中，β为实常数；i为虚数单位.NLS方程对分析求解具有一定难度，没有统一和高效的方法，在对非线性方程的各类研究中发现，非线性方程在很多情况下都不具备解析解，只有给出具体的限定条件才能得到确切的结果.关于同一个NLS方程，若给定的初始波函数不同，波函数的随时演化模式也会产生变化，为此，利用数值模拟研究NLS方程.

随着科学技术的创新，非线性薛定谔方程的研究越来越受到国内外学者的重视.张云峰[1]运用算子半群方法证明了NLS方程的解存在唯一性及解的一些性质；孟佳[2]利用有限差分法对具体的NLS方程问题展开数值求解；Borhanifar等[3]研究薛定谔方程近似解的构造，并在实验中加以验证；Ashyralyev等[4]研究含相关系数的高维分数阶薛定谔微分方程混合问题的一阶及二阶精度差分格式，并得到这些差分格式解的稳定性分析；Zisowsky等[5]建立并分析求解NLS方程的不同有限差分格式的离散人工边界条件，借助数值算例证明其稳定性和正确性.

偏微分方程领域中的数值计算方法都很经典，主要包括算子分裂法，有限元法，有限差分法等[6].有限差分法是求常(偏)微分方程及方程组的定解的方法，它较为灵活简单，普遍性强，因而方便利用计算机进行编程求解.在相关格式数值研究中，王海等[7]简要分析二阶中心差分的理论基础，在此基础上构造声波方程的该格式，建立相关模型并进行数值模拟；吴宏伟[8]证明紧致差分格式的解的相关性质，并利用该格式数值求解一类半线性抛物型方程；李华等[9]对Crank-Nicolson差分格式的误差、稳定性等展开分析证明，并联立具体的数值算例加以论证；文献[10-11]提出非线性差分格式，证明解存在唯一性和二阶收敛L∞范数，并提出一种迭代算法求解非线性差分格式；Wang[12]构造最优收敛速度的紧致有限差分格式，即L∞范数下空间上4阶及时间上2阶精度；Patel等[13]针对具体偏微分方程提出一种无条件稳定的紧致有限差分格式，并证明所提差分格式的稳定性、一致性和收敛性.

NLS方程格式守恒性一直备受学者们的重视[14-17]，张鲁明等[18-19]针对NLS方程构造新的守恒差分格式，并对该守恒格式的收敛稳定性展开证明；Lü等[20]推导出NLS方程的一种新求解方法，并利用实验证明该方法能准确保持电荷守恒、能量守恒；Ismail等[21]提出求解NLS方程的一种线性隐式守恒方法，并在数值实验中表明该方法在时间和空间上均具备二阶精度且能精确地保持能量守恒；Wang[22]提出一种求解非线性耦合薛定谔方程的能量守恒算法，并分析所提算法的可解性、稳定性和误差估计；Wang[23]提出并分析一个关于非线性耦合薛定谔方程的线性守恒差分格式；文献[24-26]针对带周期边界条件的非线性薛定谔方程，分别提出紧差分的能量守恒格式，并给出无网格比的误差估计；Gong等[27]利用Fourier拟谱方法构造求解2维非线性薛定谔方程的一个能量和质量守恒格式并加以分析；He[28]构造并分析了非线性薛定谔方程的一个质量且能量守恒的局部非连续Galerkin方法；Cui等[29]结合SAV方法构造非线性薛定谔方程的任意高阶的保结构指数Runge-Kutta方法；Wang等[30]研究两个高维薛定谔方程的傅里叶拟谱格式及方程的爆破行为.本文在一定初值、边值条件下，结合不同的差分格式对NLS方程进行数值求解.

1 数值格式的构造

考虑如下NLS方程的初值、边值问题，即

iut+uxx+β|u|2u=0，x∈R，t>0，

(1)

初值条件为

u(x，0)=u0(x)，x∈R，

(2)

边值条件为

u(x，t)→0， |x|→∞，t>0.

(3)

式(1)～(3)中：u0(x)为已知光滑函数，函数随着|x|→∞迅速向0衰减.

当|x|≥1时，方程的解飞快地向0衰减，所以可在一个有限的区域Ω=(xL，xR)上对式(1)～(2)展开数值求解，其中，xL，xR≥1，得到如下初值、边值问题，即

(4)

初值条件为

(5)

边值条件为

u(x，t)=0，x=xL或x=xR，x∈∂Ω.

(6)

式(4)～(6)的质量守恒律为

(7)

能量守恒律为

(8)

2 几种差分格式

2.1 向前Euler格式

(9)

由二阶中心差分算子和向前差分算子，有

(10)

(11)

将式(10)，(11)代入式(9)，有

(12)

结合式(5)～(6)，有

(13)

(14)

(15)

(16)

(17)

以上格式即为NLS方程的向前Euler格式，是一个非线性显式格式，记

(18)

向前Euler格式(15)～(17)的数值解在时间和空间方向分别具有1阶、2阶精度.

2.2 Crank-Nicolson格式

(19)

式(19)中：0≤n≤N-1；1≤j≤J-1.

结合式(10)及如下式(20)～(22)，即

(20)

(21)

(22)

并利用向前Euler格式类似的推导过程，有

(23)

(24)

(25)

(26)

与向前Euler格式不同，Crank-Nicolson格式是一个非线性隐式格式，Crank-Nicolson格式(24)～(26)的数值解在时间和空间方向上都具有2阶精度.

2.3 紧致差分格式

(27)

式(27)中：0≤j≤J；0≤n≤N-1.

结合式(20)～(22)，有

(28)

式(28)中：0≤n≤N-1；0≤j≤J-1；c3是与h和τ无关的常数.

对式(28)两边同时乘以Ah，经过变换有

(29)

由于

(30)

(31)

将式(31)代入式(29)，有

(32)

(33)

(34)

(35)

紧致差分格式也是一个非线性隐式格式，利用前面定义的矩阵A和H，可以将式(33)表示为

(36)

紧致差分格式(33)～(35)的数值解在时间和空间方向上分别具有2阶，4阶精度.

3 守恒性

定理1Crank-Nicolson格式(24)～(26)精确保离散质量守恒和能量守恒，质量守恒和能量守恒分别为

(37)

(38)

式(37)～(38)中：n=0，1，2，…，N.

证明:式(24)的紧形式为

(39)

对上式取虚部，有

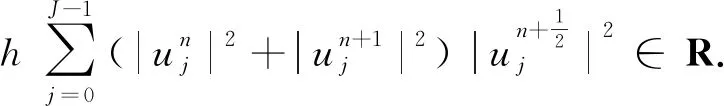
将(un+1-un)与式(39)两边同时作内积，并取实部，有

(40)

定理2紧致差分格式(34)～(36)精确保离散质量守恒和能量守恒，质量守恒和能量守恒分别为

(41)

(42)

将式(36)的两边与(un+1-un)作内积并取实部，得

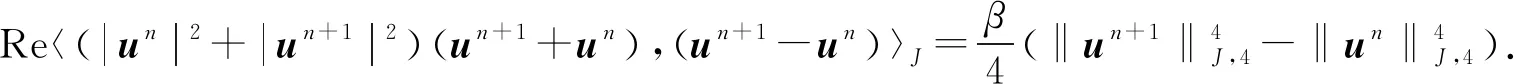
4 数值实验

4.1 孤立波的演化实验

图1 初始条件下t=0 s时的孤立波波形

(a) t=1 s (b) t=10 s

Crank-Nicolson格式和紧致差分格式的孤立波波形分别如图3，4所示.

(a) t=1 s (b) t=10 s

(a) t=1 s (b) t=10 s

由图2～4可知：当t=10 s时，向前Euler格式所得的孤立波波形有一些振荡，可能是因为向前Euler格式作为显格式，对差分步长较敏感.因此，相对其他两种格式而言，向前Euler格式稍显不足.

当t=10 s时，选取时间步长(τ=0.000 01)继续采用向前Euler格式进行数值模拟，孤立波波形，如图5所示.当t=10s时，孤立波波形随着时间步长τ的减小，振荡越弱即波形更加稳定.

图5 向前Euler格式在τ=0.000 01的孤立波波形

4.2 守恒量的保持实验

(a) 总质量 (b) 质量误差

(a) 总质量 (b) 质量误差

由图6，7可知：Crank-Nicolson格式和紧致差分格式均能很好地保持离散质量守恒和能量守恒.

4.3 数值格式的计算效率实验

5 结论

分别利用经典的向前差分算子、二阶中心差分算子、Crank-Nicolson方法和紧致差分算子构造了向前Euler格式、Crank-Nicolson格式和紧致差分格式.引用守恒性相关理论知识证明了Crank-Nicolson格式和紧致差分格式精确保持离散质量守恒和能量守恒.

通过数学软件MATLAB，分别对3种格式进行了孤立波的数值实验和计算，并研究了Crank-Nicolson格式和紧致差分格式对守恒量的保持.虽然3种格式均能对NLS方程进行数值求解，但是具有不同的特性.向前Euler差分格式作为非线性显式格式，易于理解和编程，并且计算时间较少.而Crank-Nicolson格式和紧致差分格式都是非线性隐式格式，通过数值实验可以验证它们都能够精确保持离散质量守恒和能量守恒，与理论证明相符合.

这些格式不仅能应用于NLS方程，还能应用于偏微分方程领域的诸多方程中，如KdV方程、Klein-Gordon方程等.每种差分格式都具有不同的优劣性，在具体的实际情况下，可采用较为理想的差分格式进行数值计算.