基于等效样本和实仿融合的现场小子样试验制导精度评估方法

宁小磊，吴颖霞

(中国华阴兵器试验中心，华阴 714200)

随着高新技术的迅速发展，在常规制导兵器的论证、研制过程中引入了惯性导航系统、成像导引头等昂贵部件[1]，大大提升了常规制导兵器的作战能力和作战效能，但同时装备单子样价格也日益昂贵。在装备鉴定定型阶段，受试验消耗约束，现场能够获取的试验样本越来越少，若仍采用传统的纯粹依据现场试验评估装备性能指标的试验方法[2]，存在试验评估误差较大、试验鉴定风险较高等问题。

Bayes 方法通过融合仿真先验信息可提高现场小子样试验评估精度[3-6]，但Bayes 方法在融合评估时，仍存在先验分布如何科学确定的问题，尤其当先验信息失真时，估计精度甚至下降。针对先验分布的确定问题，现有文献[7-9]提出了采用加权自助抽样技术构造先验分布；通过引入修正幂参数构造带幂函数的先验分布，控制验前信息对验后估计的影响；通过加权计算仿真先验分布和无信息先验分布，构造混合先验分布；通过引入先验信息可信度C构造了先验分布，并改进了后验加权系数的计算方法。现有文献[7-9]提出的一些科学构造先验分布的有效方法，一定程度上提高了Bayes 估计性能。但这些方法本质是通过加入无信息先验分布减少仿真先验参加计算后验参数的权重，确保Bayes 估计精度，很显然这是一种比较保守的改进策略，不能充分利用先验信息。

针对上述问题，提出了一种基于等效样本和实仿融合的现场小子样试验制导精度评估方法。该方法在仿真可信度C、统计理论和评估精度约束下，提出由仿真可信度C引起的评估误差E1 和仿真抽样引起的评估误差E2 共同度量仿真先验精度。使用等效样本表征E1，仿真抽样样本表征E2，并将其带入Bayes融合框架完成后验分布的精确估计。根据Kalman 滤波收敛性理论给出了该方法合理性的证明。最后，通过示例对改进方法与传统方法的估计性能进行了比较，验证了本文方法的有效性和正确性。

1 Bayes 方法与问题分析

1.1 Bayes 方法

Bayes 方法可以利用先验信息和现场数据实现参数后验统计推断[5-6,10]，Bayes 统计推断过程如下[10]

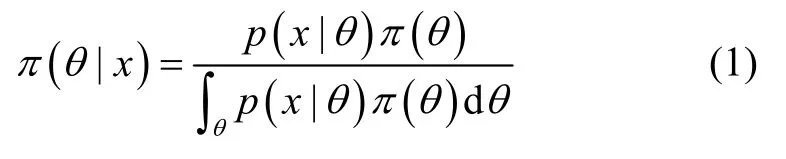
式中，θ为未知量；x为现场抽样样本；π(θ|x)为后验分布；π(θ)为先验分布；p(x|θ)为样本信息；为边缘密度函数。

在式(1)中，先验分布π(θ)反映了抽样前对θ的认识，后验分布π(θ|x)反映了抽样后对θ的认识。Bayes方法就是通过现场样本x对θ认识的一种调整。因此后验分布π(θ|x)可以看作是用总体信息和样本信息对先验分布π(θ)调整的结果[10]。使用Bayes 方法融合仿真数据与现场数据综合评估时，将仿真数据作为仿真先验信息，然后使用现场数据调整先验分布，得到后验分布，用框图表示Bayes 融合过程如图1 所示[10]。

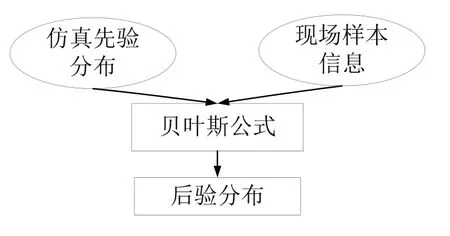
图1 贝叶斯原理示意图Fig.1 Bayesian principle diagram

由于制导精度一般服从正态分布，下面给出正态分布由共轭先验到后验分布的Bayes 统计推断。

1.2 Bayes 方法融合评估时的问题分析

对式(2)进行分析可见，μ2实际上是μ0和μ1的加权和，加权系数分别是1-k和k，由先验信息精度和现场样本精度共同确定。假设σ2=0.5，=0.45，图2 给出了该条件下的权系数计算结果。

从图2 可见，随着现场样本量n增大，仿真先验权系数急剧下降；当现场样本量n增大到10 以后，仿真先验系数大约为0.1，对计算后验分布参数的贡献已经很小了；当n= 1时，两系数才大致相当。很显然，这种权系数分配并不是最优的，比如当仿真先验精度较高时，在现场样本估计精度超过仿真先验精度时，才应该赋给现场样本更大的权重。

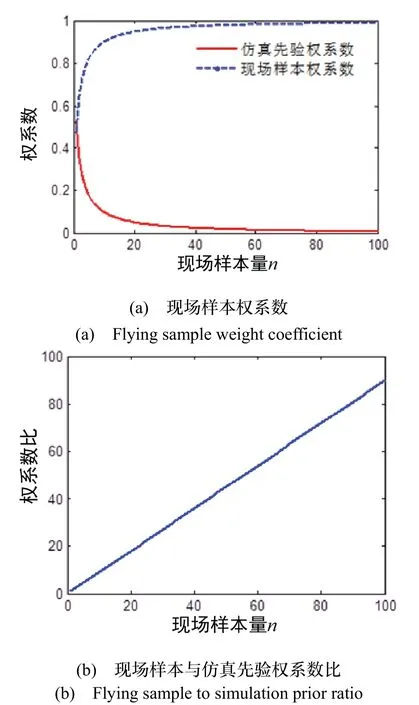
图2 权系数计算结果示意图Fig.2 Weight coefficient calculation result

2 基于等效样本和实仿融合的Bayes 统计推断

2.1 改进思路

对仿真先验分布而言，仿真可信度C是度量μ0偏离μ程度的参数，很显然仿真可信度C越高，则μ0的精度越好，反之μ0的精度就越差，因此可以基于仿真可信度C建立表征μ0的精度模型。从μ1的精度公式可见，抽样样本量n是精度的数学实质反映，因此，也可由一个“虚拟”的抽样样本量m表征先验分布μ0的精度，我们将这个抽样样本量m称为等效样本（Equivalent Sample，ES），它的物理意义是从具有仿真可信度C的仿真试验系统中抽样，其评估误差相当于现场飞行m个试验样本的评估误差。这样就可以基于评估精度建立表征μ0精度的模型如下

将式(5)带入式(4)计算权系数，就可以得到最优后验估计结果。

2.2 等效样本的确定

假设母体分布函数为 N （μ,σ2），仿真先验分布函数为仿真试验系统可信度为C。从中抽取M个仿真样本模拟仿真试验，其估计精度为从 N （μ,σ2）中抽取m个现场样本模拟飞行试验，其估计精度为σ2/m，则当

根据上述描述，很明显可得到

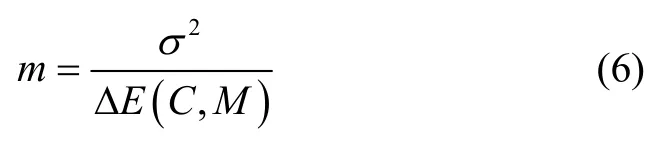
由式(6)可见，已知σ2，m只与 ΔE（C,M）有关，而，一般情况下很小，可忽略不计，则有

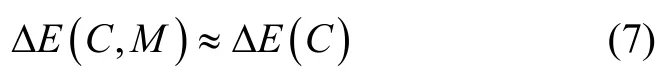
由式(7)可见，仿真试验评估误差ΔE主要由仿真可信度C表征。建立仿真可信度C与仿真评估误差ΔE（C）之间的关系模型如下

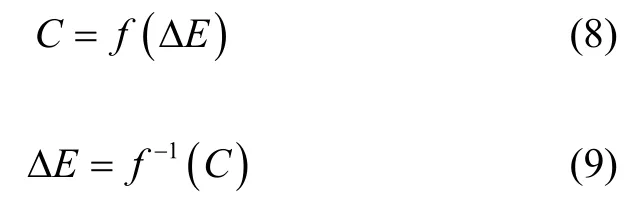
式中，f（ · ）为ΔE与C之间的关系模型；f-1（ · ）为f（· ）的反函数。式(8)最重要的物理意义是建立了仿真可信度C与仿真评估指标误差之间的关系模型，仿真可信度C是仿真评估指标误差的量化度量。

我们给出f（· ）一种简单关系模型如下

则有

仿真可信度评估是系统仿真与建模领域比较复杂的问题，一般根据工程应用背景和仿真模型验证方法给出科学度量，本文主要研究数据融合算法，对验证方法不作深入探讨。

2.3 统计推断

综上，基于等效样本和实仿融合的Bayes 统计推断公式如下

3 评估精度分析

3.1 权系数最优分配的理论分析

假设有如下线性动态系统模型

式中，Φk,k-1为一步转移矩阵；Γk-1为系统噪声驱动矩阵；Hk为量测阵；Wk-1为系统噪声；Vk-1为量测噪声，且满足

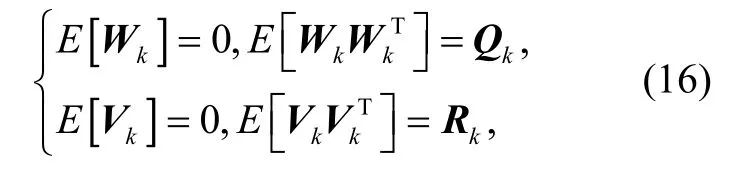
当Φk,k-1= 1，Γk-1= 1，Hk=1时，式(16)变为

式(15)所示线性系统的Kalman 滤波实现为[11]

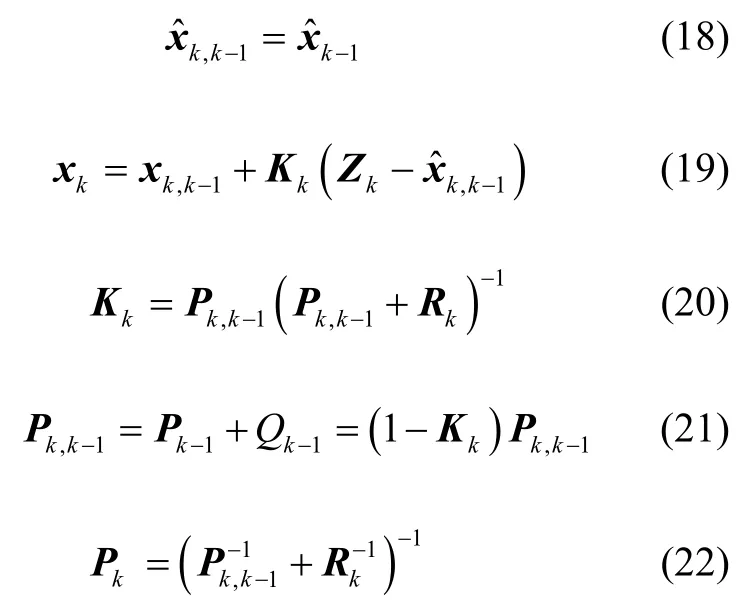
将式(2)转化成如下形式

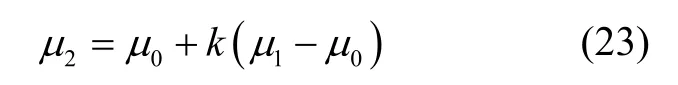
其对应的线性动力学模型为

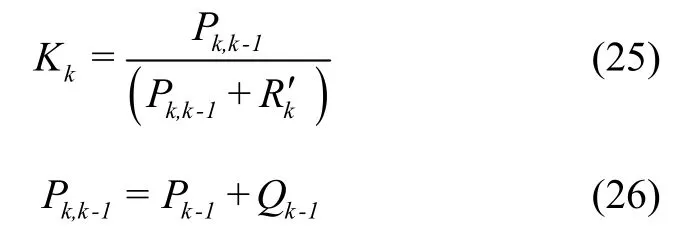
由式(26)可见，Pk,k-1由Pk-1,Qk-1两部分组成，其中，M为仿真抽样样本，一般M很大，因此，Qk-1很小，即仿真抽样误差很小。Pk-1是k- 1的最优估计误差，可理解为仿真系统误差，由仿真可信度C引起。

3.2 估计精度分析

对基于等效样本和实仿融合的Bayes 统计推断进行精度分析，假设有权系数偏离量δk，则有均方误差偏离量δP，为

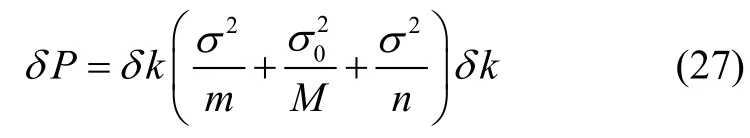
根据式（22），可得到本文方法的估计精度为

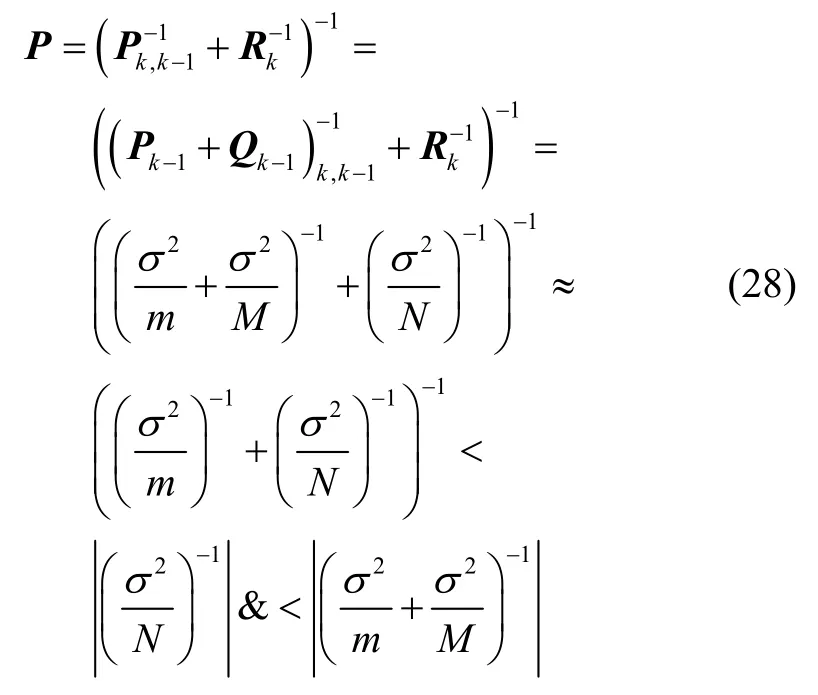
式(28)的工程意义在于：现场N个样本，仿真等效样本为m，则基于等效样本的实仿融合评估精度相当于现场N+m个样本的评估精度。

4 示例分析与比较

4.1 示例场景描述

选择示例比较分析改进方法与现有方法在估计性能上的差别，示例场景描述如下：

总体分布为 N （μ,σ2），μ=0.4，σ2=0.5；先验分布为总体分布与先验分布为之间的差异为则根据式(6)得m≈ 10。从 N （μ,σ2）中抽取现场样本x1,x2, … ,xn，n= 7，令则现场样本分布为 N （μ1,σ2）。

用均方根误差RMSE（R）度量Bayes 估计精度，RMSE 计算公式如下

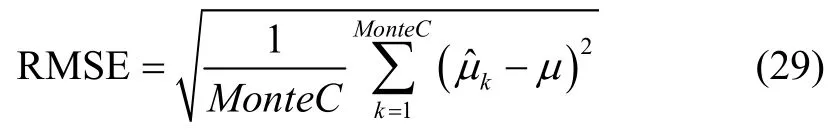
式中，MonteC为蒙特卡洛实验次数；为估计值；μ为真值。

4.2 估计精度RMSE（R）实验

运行MonteC= 60次，得到各种方法的RMSE 如下 ：RMSE1=0.2082；RMSE2=0.1793；RMSE3=0.0883，其中，RMSE1为基于现场样本统计的均方根误差；RMSE2为Bayes 方法的均方根误差；RMSE3为本文方法的均方根误差。可见，本文方法的RMSE3小于现有两种主要方法，说明其估计精度高于现有方法。图3 给出了不同估计方法对μ的估计结果及估计误差，估计次数为60 次，估计误差Error= abs（-μ），其中，为估计值， abs （ · ）为取绝对值运算，从图3 可见，本文方法的估计精度较高。

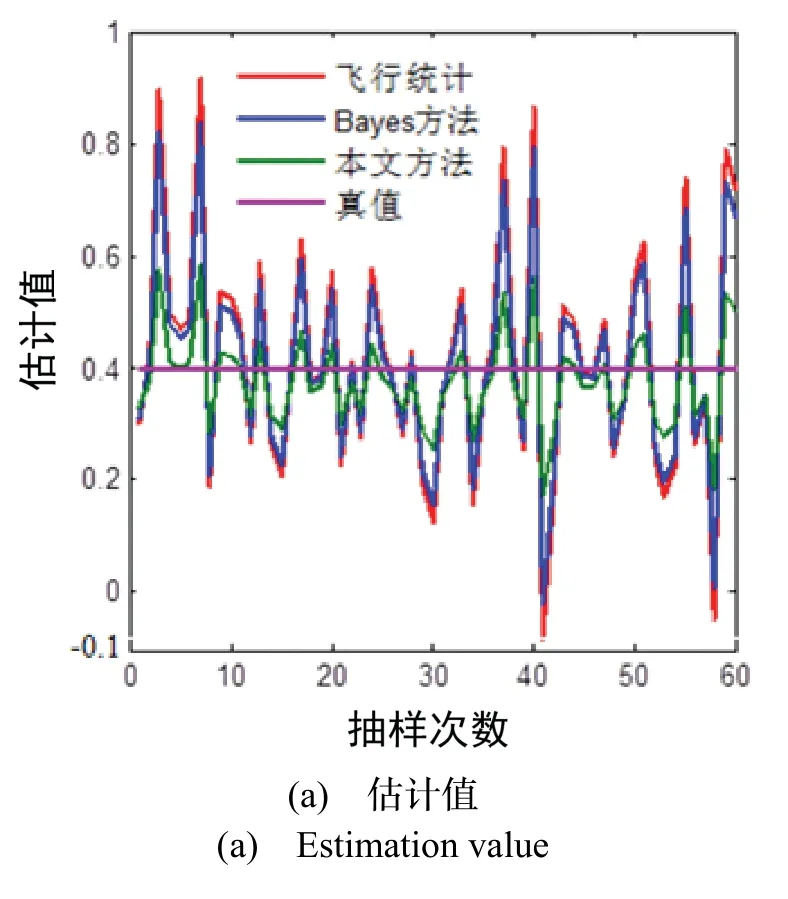
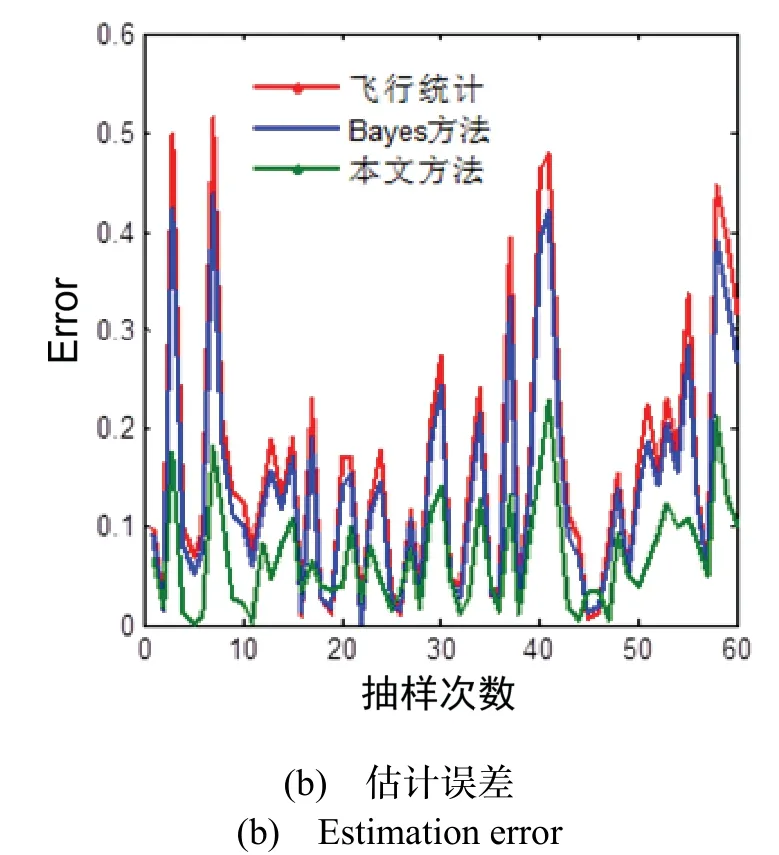
图3 估计结果Fig.3 Estimation result

60 次抽样中有7 次估计误差比Bayes 方法大，这是因为小子样现场样本估计结果非常高所致，具有随机效应。7 次抽样具体估计结果见表1 所示。

表1 7 次抽样及估计结果Tab.1 7 times test sample and estimation result

一次现场抽样样本如下：x=[1.0245, 0.7947，0.2864, 0.8804, 0.2280，0.8199, 0.9733]，则μ1=0.7153，=0.6653，μ2′ =0.5004，其中，μ2′为Bayes 估计结果，μ2′为本文方法估计结果，可见μ1′相比μ1′误差较小，说明本文方法的有效性。

4.3 现场样本量n 对估计精度的影响效应实验

图4 给出了估计误差随现场抽样样本量n的变化过程，图5 给出了加权系数随现场抽样样本量n的变化规律，其中虚线为现场加权系数，实线为仿真加权系数。

由图4 可见，随着现场样本量n的增加，μ1的估计精度逐渐提高，Bayes 方法和本文方法的估计精度均逐渐提高，最后逐渐逼近现场样本估计精度，这是因为现场样本系数k逐渐逼近1，此时估计结果μˆ2主要由μ1决定。但当n较小时，很显然本文方法估计精度好于Bayes 方法。

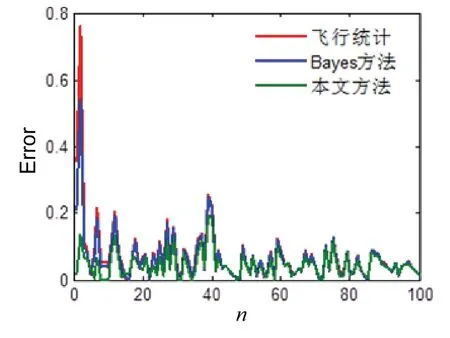
图4 估计误差随现场样本量n 的变化规律Fig.4 Relationship curve between estimation error and flying test sample n

从图5 可见，Bayes 方法权系数分配中，n很小时现场权系数非常大，导致仿真先验对后验分布参数计算贡献很小，这样分配系数显然不合理，因为此时仿真先验比现场样本估计精度要高，应当赋予更大的权系数；而本文方法中，当10n= 时，现场样本系数与仿真先验系数大致相当；当n较小时，仿真先验权系数大于现场样本权系数，后验参数计算大部分由仿真先验值决定。

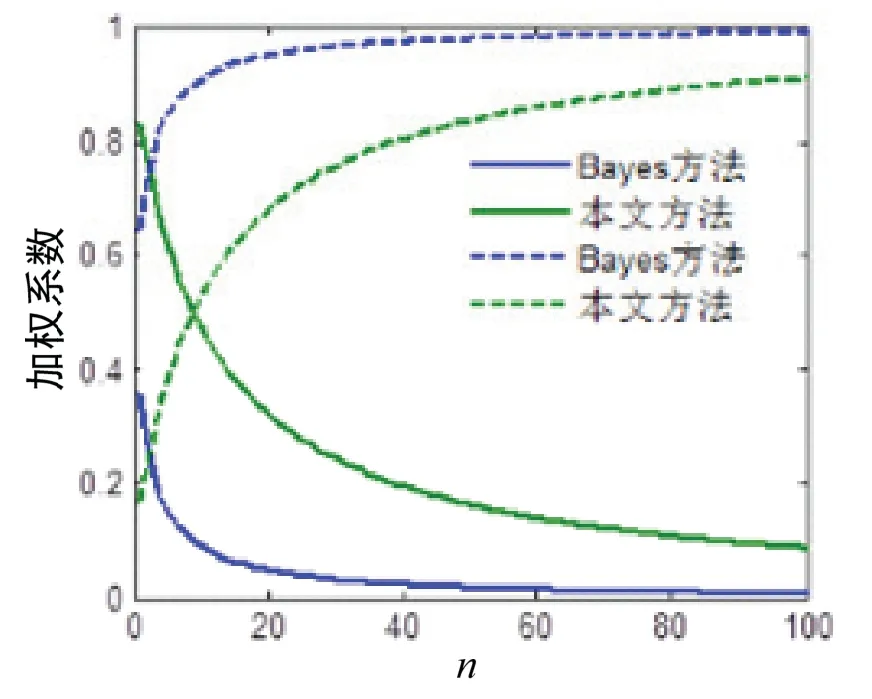
图5 加权系数随现场样本量n 的变化规律Fig.5 Relationship curve between weight coefficient and flying test sample n

4.4 仿真先验对估计精度的影响效应实验

用μ0=0.2:0.02:0.8模拟不同精度（仿真先验精度dμ=-0.2：0.02：0.4）的先验分布，其余场景条件不变进行实验。

图6 给出了估计误差与不同精度仿真先验0μ、现场样本量n的变化曲面。从图6 可见，两种方法的估计精度随着现场样本量n增大均逐渐提高；本文方法的估计精度高于Bayes 方法，尤其在现场样本量n较小时，估计精度明显好于Bayes 方法。

图7 给出了等效样本m与不同精度仿真先验μ0、现场样本量n的变化曲面。从图7 可见，当μ0=0.4时，等效样本m最大，这是因为此时μ=μ0，其中，μ为真值。随着μ0相对μ增大或减小，m均减小。

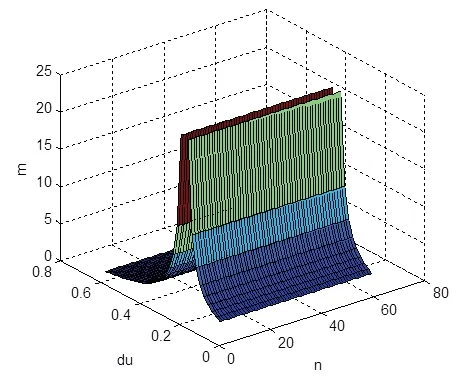
图7 等效样本m 与仿真先验误差 μ0、现场样本量n 的关系曲面Fig.7 Relationship curve between equivalent sample m and simulation prior, flying test sample n

图8 给出了现场样本权重k与不同精度仿真先验μ0、现场样本量n的变化曲面。

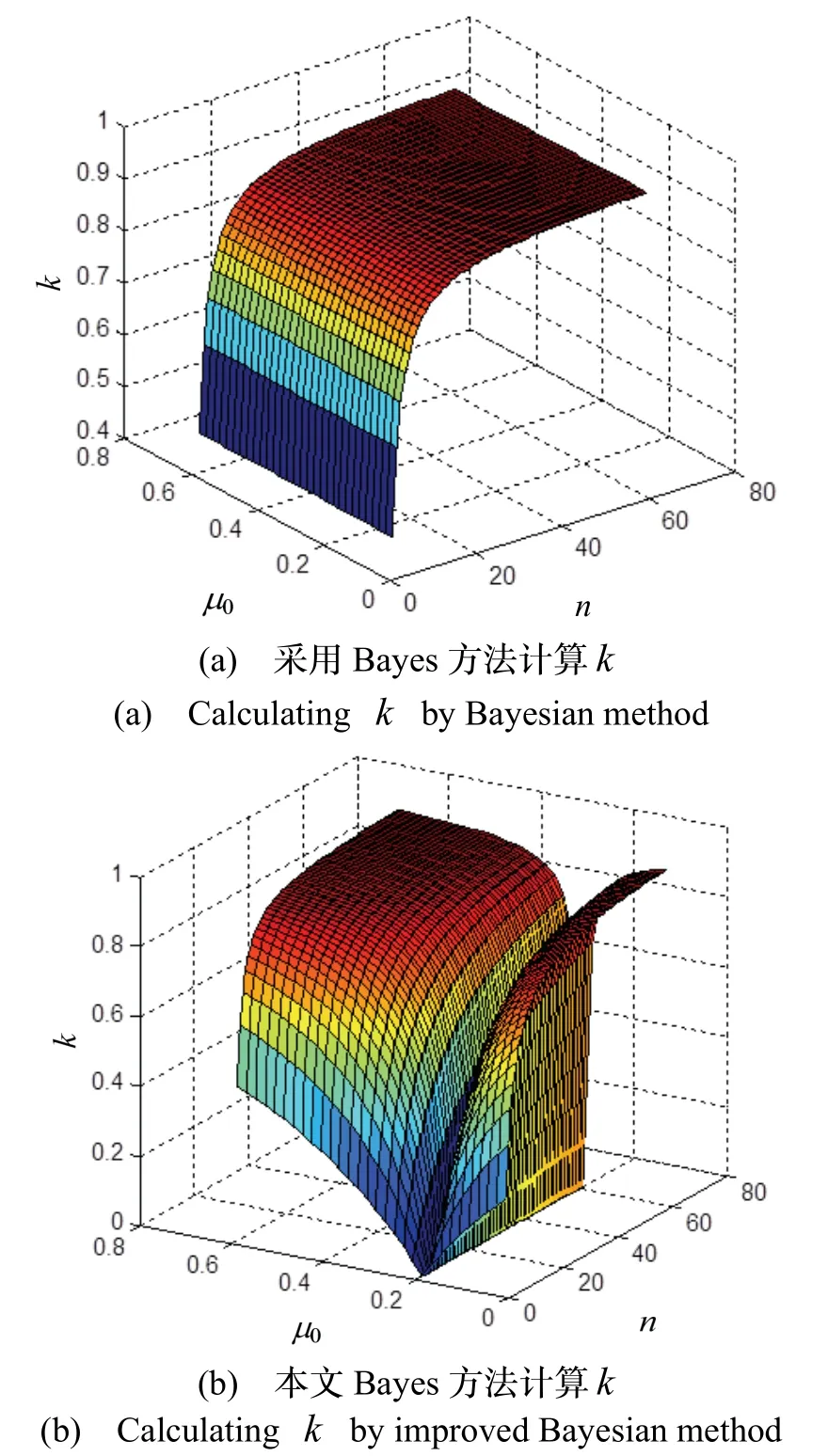
图8 权系数k 与仿真先验误差 μ0、现场样本量n 的关系曲面Fig.8 Relationship curve between weight coefficient k and simulation prior, flying test sample n

从图8 可见，Bayes 方法对仿真先验μ0不敏感，但随着现场样本量n增大k急剧增大，此时现场样本在后验分布参数计算中起主要作用；本文方法在μ0=0.4时k最小，这是因为此时μ=μ0，仿真先验分布与真实分布相同，仿真样本相当于实际抽样样本；随着μ0相对μ增大或减小，k逐渐增大，这是因为仿真先验不精确时，应增大现场样本权重；随着现场样本量n增大，两种方法中k均逐渐增大。

4.5 仿真可信度C 对估计精度的影响效应实验

用dμ表示仿真先验误差，度量仿真可信度C评估误差；用Δμ表示仿真先验误差评估精度，其余场景条件不变进行实验。

图9 给出了仿真先验误差dμ引起的Bayes 估计误差曲面图。由图9 可见，随着dμ增大，估计精度下降，但n能够在一定程度上弥补这种误差。图10给出了仿真先验误差dμ引起的均方根误差RMSE。由图10 可见，随着dμ增大，RMSE 增大。由图9、10 可见，要保证一定精度，就必须精确表征仿真先验。

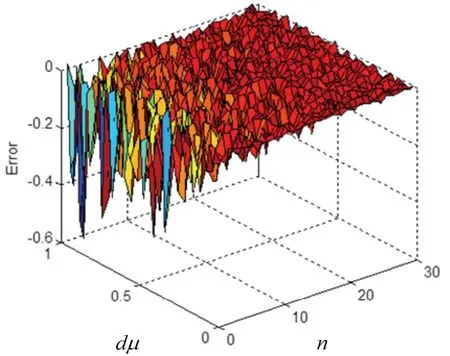
图9 估计误差与dμ、n 的关系曲面Fig.9 Relationship curve between estimation error,dμ and n

图10 RMSE 与dμ、n 的关系曲面Fig.10 Relationship curve between RMSE,dμ and n

图11 给出了等效样本计算误差dm与仿真先验误差dμ、现场样本n的关系；图12 给出了现场样本权系数计算误差dk与仿真先验误差dμ、现场样本n的关系；图13 给出了命中概率评估误差dP与仿真先验误差dμ、现场样本n的关系。由图11-13 可见，随着dμ增大，等效样本误差dm、权系数计算误差dk、命中概率评估误差dP均增大（同样的，减小dμ，即提高仿真系统可信度C，可以提高命中概率评估精度），但随着现场试验样本n增加，dP逐渐减小。

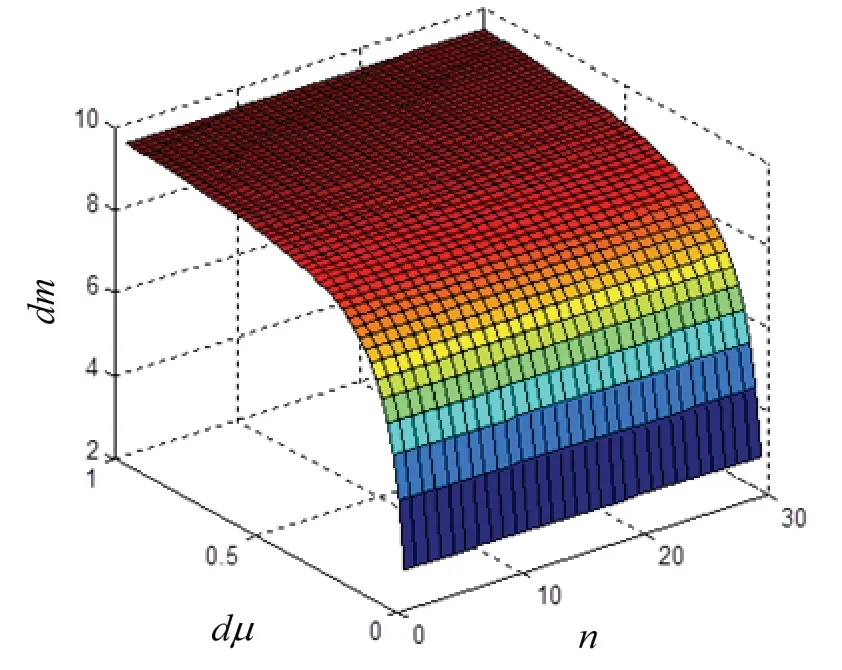
图11 等效样本误差dm 与dμ、n 的关系曲面Fig.11 Relationship curve between ES dm, dμ and n

图12 权系数计算误差dk 与dμ、n 的关系曲面Fig.12 Relationship between weight coefficient calculation error dk, dμ and n

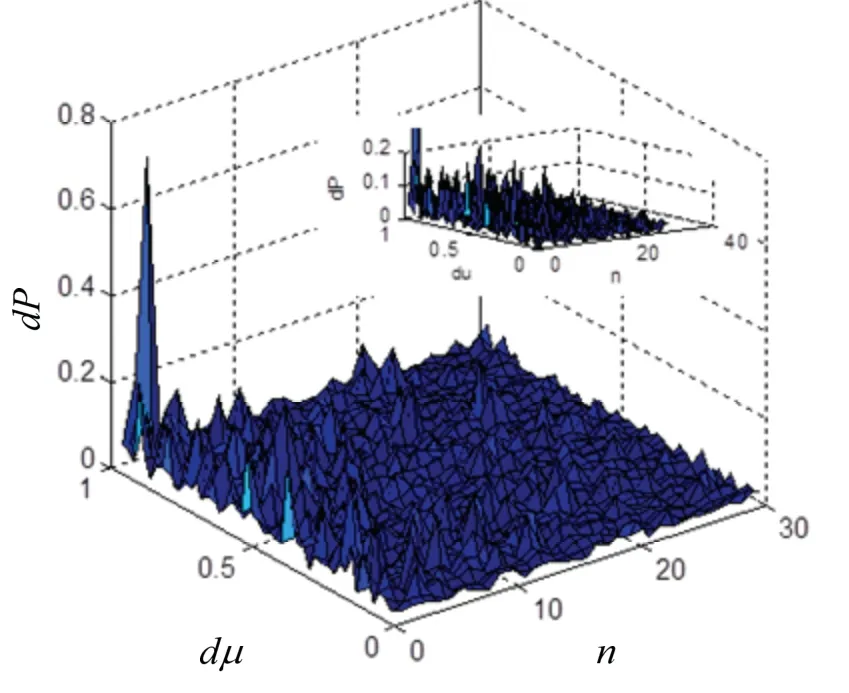
图13 命中概率估计误差dP 与dμ、n 的关系曲面Fig.13 Relationship curve between hit probability evaluationerror dP, dμ and n

图14 给出了仿真先验评估误差为Δμ时与仿真先验评估误差Δμ= 0时（此时表示能够精确评估仿真先验）的命中概率评估误差之差ΔP与仿真先验评估误差Δμ、现场样本n的关系。由图14 可见，随着仿真先验评估误差Δμ减小，能够提高命中概率评估精度，这说明提高仿真系统可信度C评估精度，与增加现场试验样本量n、提高仿真系统可信度C一样，在一定程度上可以降低试验评估误差。

图14 命中概率评估误差之差ΔP 与Δμ 、n 的关系曲面Fig.14 Relationship curve between the errorΔPof hit probability evaluation error, Δμ and n

5 工程应用案例

使用文献[9]给出的工程案例数据进行应用对比分析。案例场景如下：

案例1[9]在武器落点精度试验中，6 个实际纵向落点偏差样本为（单位：m）：x=[0.25， 9.3， 5.5， 4.0， 1.1， 2.2]；补充样本为x0=[10.0， 8.1， 13.1， 3.3， 6.5， 4.6， 4.8， -10.6， -8.8， -10.7]；这里，补充样本服从的分布与真实试验的分布有一定差异。采用各种方法得到的估计结果见表2 所示。

表2 估计结果（单位：m）Tab.2 Estimation result（Unit: m）

案例2[9]在武器落点精度试验中，6 个实际纵向落点偏差样本为（单位：m）：x= [0.77， 5.60， 14.64， -9.79， 17.6， -12.1]；补充样本为x0=[-11.32， -1.65， 12.97， -27.91， -10.88， 8.32， -14.95， 3.61， -5.03， 0.28]；这里补充样本服从的分布与真实试验的分布是相同的，都是 N （0,102）。采用各种方法得到的估计结果和表3 所示。由表3 可见，本文方法μˆ 估计精度较好，使用式(2)估计方差精度较差。

表3 估计结果（单位：m）Tab.3 Estimation result（Unit: m）

6 结 论

本文针对Bayes 方法应用于仿真数据和现场试验数据融合评估时存在的仿真数据容易“淹没”现场试验数据、估计结果不是最优估计值等问题，提出了一种基于等效样本和实仿融合的现场小子样试验制导精度评估方法。该方法为了提高融合评估精度和可靠度，在仿真可信度C、统计理论和仿真评估精度约束下，将仿真验前信息折算成等评估精度下的飞行样本量，精确度量了仿真先验信息精度，并将其引入Bayes 融合框架实现了对后验分布参数的精确估计，从而解决了Bayes 方法直接将仿真先验分布方差作为度量仿真先验信息的精度参数参与计算后验加权系数导致的估计精度不高、先验信息失真时估计精度甚至下降等问题。根据kalman 滤波收敛性理论证明了现场样本权系数计算的最优性，并给出了估计误差模型。通过示例对改进方法与传统方法的估计性能进行了比较，验证了本文方法的有效性和正确性。