关于不定方程x3±1=7qy2

管 训 贵

(泰州学院数理学院，江苏 泰州 225300)

关于不定方程

x3±1=Dy2(D>0，且D无平方因子)

(1)

的整数解，迄今已有丰富的研究成果[1-18].但当D=7q，q为非7的奇素数时，方程(1)的求解问题，目前只有一些零散的结果．

本文讨论了不定方程x3±1=7qy2的整数解，并给出下列结论.

定理1设奇素数q≡11，23，29，53，65，71，95，107，113，137，149，155(mod 168)，则不定方程

x3+1=7qy2

(2)

仅有整数解(x，y)=(-1，0)．

考虑100以内的奇素数q，得到如下推论1.

推论1当q=3，5，11，13，17，19，23，29，41，43，53，59，61，71，73，83，89，97时，方程(2)除开q=5仅有整数解 (x，y)=(-1，0)和 (19，±14)以及q=13仅有整数解(x，y)=(-1，0)和(4367，±30252)外，其他情形仅有整数解(x，y)=(-1，0)．

定理2设奇素数q≡11，23，29，53，71，95，107，149，155，167(mod 168)，则不定方程

x3-1=7qy2

(3)

仅有整数解(x，y)=(1，0)．

考虑100以内的奇素数q，得到如下推论2.

推论2当q=3，5，11，13，17，19，23，29，31，37，41，43，53，59，61，67，71，83，89时，方程(3)除开q=17仅有整数解(x，y)=(1，0)和(18，±7)外，其他情形仅有整数解(x，y)=(1，0)．

1 若干引理

引理1设D为正整数，q≡2(mod 3)为奇素数，且q|D，则方程x2±x+1=Dy2无整数解．

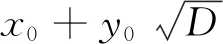
引理3i)设q为奇素数，且q∈{3，13，61，73，97}或q≡5，11，17，19，23(mod 24)，则不定方程组

x+1=u2，x2-x+1=7qv2，gcd(u，v)=1

(4)

无整数解．

ii)设q为奇素数，且q∈{3，13，37，61，73，97}或q≡5，7，11(mod 12)，则不定方程组

x-1=u2，x2+x+1=7qv2，gcd(u，v)=1

(5)

无整数解．

证明i)由x=u2-1≡-1，0，3(mod 8)知，x2-x+1≡3，1，7(mod 8)，此时7q≡3，1，7(mod 8)，即q≡5，7，1(mod 8)，若q≡3(mod 8)，则(4)无整数解.再根据引理1，若q≡2(mod 3)，则(4)也无整数解.于是q=3或q≡5，11，17，19，23(mod 24)时，(4)无整数解．

将x=u2-1代入第二式得u4-3u2+3=7qv2，即(2u2-3)2-7q(2v)2=-3．

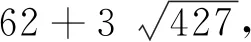
ii)由x=u2+1≡1，2(mod 4)知，x2+x+1≡3(mod 4)，此时7q≡3(mod 4)，即q≡1(mod 4).若q≡3(mod 4)，则(5)无整数解.再根据引理1，若q≡2(mod 3)，则(5)也无整数解.于是q=3或q≡5，7，11(mod 12)时，(5)无整数解．

将x=u2+1代入第二式得u4+3u2+3=7qv2，即(2u2+3)2-7q(2v)2=-3．

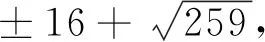
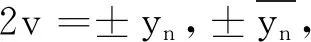
当q=61时，(2u2+3)2-427(2v)2=-3.由i)中q=61的证明知，(5)无整数解.引理3得证．

引理4i)设q为奇素数，且q∈{3，19，31}或q≡1，5，11，13，17，23，25，29，37，41，43，47，53，

59，61，65，67，71，73，79，83，85，89，95，97，101，107，109，113，121，125，127，131，137，143，145，149，151，

155，157，163，167(mod 168)，则不定方程组

x+1=7u2，x2-x+1=qv2，gcd(u，v)=1

(6)

除开q=3时仅有整数解(x，u，v)=(-1，0，±1)外，其他情况均无整数解．

ii)设q为奇素数，且q∈{3，19}或q≡1，5，11，13，17，23，25，29，37，41，43，47，53，59，61，65，67，71，79，83，85，89，95，101，107，109，113，121，125，127，131，137，143，149，151，155，157，163，167(mod 168)，则不定方程组

x-1=7u2，x2+x+1=qv2，gcd(u，v)=1

(7)

除开q=3时仅有整数解(x，u，v)=(1，0，±1)外，其他情况均无整数解．

证明i)q=3的证明见后文引理11 i)的证明.下证其他情形．

由x=7u2-1≡2，3(mod 4)知，x2-x+1≡3(mod 4)，此时q≡3(mod 4).若q≡1(mod 4)，则(6)无整数解．

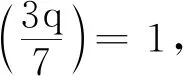
再根据引理1，若q≡2(mod 3)，则(6)也无整数解.

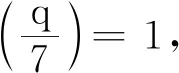
若q=19，则将(6)第一式代入第二式得(14u2-3)2-19(2v)2=-3.

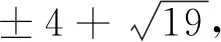
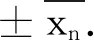
容易验证下式成立：

xn+2=340xn+1-xn，x0=4，x1=1421.

(8)

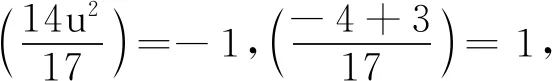
ii)q=3的证明见后文引理11 ii).q=19的证明见文献[16].q=31的证明见文献[22].下证其他情形．

由x=7u2+1≡1，0，5(mod 8)知，x2+x+1≡3，1，7(mod 8)，此时q≡1，3，7(mod 8).若q≡5(mod 8)，则(7)无整数解.再根据引理1，若q≡2(mod 3)，则(7)也无整数解.于是q≡5，11，13，17，23(mod 24)时，(7)无整数解．

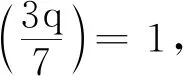
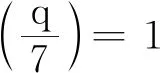
引理5i)设q为奇素数，且q∈{3，5，17，41，43，59，83，89}或q≡11，13，19，23，29，31(mod 42)，则不定方程组

x+1=qu2，x2-x+1=7v2，gcd(u，v)=1

(9)

除开p=5时仅有整数解(x，u，v)=(19，±2，±7)外，其他情况均无整数解．

ii)设q为奇素数，且q∈{3，5，17，37，41，43，59，67，79，83，89}或q≡11，13，19，23，29，31(mod 42)，则不定方程组

x-1=qu2，x2+x+1=7v2，gcd(u，v)=1

(10)

除开q=17时仅有整数解(x，u，v)=(18，±1，±7)外，其他情况均无整数解．

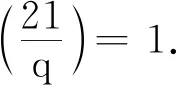
将第一式代入第二式得

(2qu2-3)2-7(2v)2=-3.

(11)

2qu2-3=±xn.

(12)

容易验证下式成立：

xn+2=16xn+1-xn，x0=2，x1=37.

(13)

若2|n，则由(13)知2|xn，此时(12)式不成立．

2qu2=±1(mod 3).

(14)

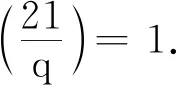
将第一式代入第二式得

(2qu2+3)2-7(2v)2=-3.

(15)

类似i)中(11)式的讨论，对(15)式只需考虑

2qu2+3=±xn.

(16)

且有(13)式成立．

若2|n，则由(13)知2|xn，此时(16)式不成立．

2qu2≡±1(mod 3).

(17)

当n≡1(mod 4)时，对递归序列(13)取模16，有xn≡5(mod 16)，此时qu2≡1(mod 8)，可得q≡1(mod 8)，故当q=5，37，59，67，79，83时，均不成立．

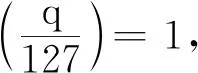
若q=17，则由文献[13]的讨论知n=1，此时(10)仅有整数解(x，u，v)=(18，±1，±7)．

引理6[20]设p是一个奇素数，则方程4x4-py2=1除开p=3，x=y=1和p=7，x=2，y=3外，无其他的正整数解．

引理7[20]方程x2-3y4=1仅有整数解(x，y)=(±2，±1)，(±7，±2)，(±1，0)．

引理8[20]设p是一个奇素数，则方程x4-py2=1除开p=5，x=3，y=4和p=29，x=99，y=1820外，无其他的正整数解．

引理9[21]设b，d>1且不是平方数，则方程b2x4-dy2=1至多有一组正整数解(x，y)．

引理10i)设q为奇素数，且q=3或q≡1，5，11，13，17，19，23(mod 24)，则不定方程组

x+1=21qu2，x2-x+1=3v2，gcd(u，v)=1

(18)

除开q=13仅有整数解(x，u，v)=(-1，0，±1)，(4367，±4，±2521)外，其他情况均仅有整数解(x，u，v)=(-1，0，±1)．

ii)设q为奇素数，且q=3或q≡5，7，11，13，17，19，23(mod 24)，则不定方程组

x-1=21qu2，x2+x+1=3v2，gcd(u，v)=1

(19)

除开q=181仅有整数解(x，u，v)=(1，0，±1)，(60817，±4，±35113)外，其他情况均仅有整数解(x，u，v)=(1，0，±1)．

证明i)将(18)的第一式代入第二式得(2v)2-3(14qu2-1)2=1，故有

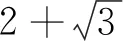
14qu2=yn+1.

(20)

容易验证下列各式成立：

xn+2=4xn+1-xn，x0=1，x1=2，

(21)

yn+2=4yn+1-yn，y0=0，y1=1，

(22)

xn+1=2xn+3yn，yn+1=xn+2yn，

(23)

(24)

xn-1=2xn-3yn，yn-1=-xn+2yn.

(25)

若n≡0(mod 2)，则由(22)知yn≡0(mod 2)，此时(20)式不成立．

又因gcd(x2m，y2m+1)=gcd(x2m，x2m+2y2m)=gcd(x2m，2y2m)=1，所以下列情形之一成立：

x2m=7qa2，y2m+1=b2，u=ab，gcd(a，b)=1；

(26)

x2m=a2，y2m+1=7qb2，u=ab，gcd(a，b)=1；

(27)

x2m=7a2，y2m+1=qb2，u=ab，gcd(a，b)=1；

(28)

x2m=qa2，y2m+1=7b2，u=ab，gcd(a，b)=1.

(29)

对于(29)，由(23)得，y2m+1=x2m+2y2m，故有7b2=qa2+2y2m，即

7b2-qa2=2y2m.

(30)

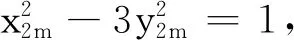
若n≡-1(mod 4)，令n=4m-1(m∈Z)，则由(23)、(24)、(25)式可得

14qu2=y4m-1+1=-x4m+2y4m+1=

2y2m(2x2m-3y2m)=2y2mx2m-1，

即7qu2=x2m-1y2m.

又因为gcd(x2m-1，y2m)=gcd(2x2m-3y2m，y2m)=gcd(2x2m，y2m)=2，所以下列情形之一成立：

x2m-1=2a2，y2m=14qb2，

u=2ab，gcd(a，b)=1；

(31)

x2m-1=14qa2，y2m=2b2，

u=2ab，gcd(a，b)=1；

(32)

x2m-1=2qa2，y2m=14b2，

u=2ab，gcd(a，b)=1；

(33)

x2m-1=14a2，y2m=2qb2，

u=2ab，gcd(a，b)=1.

(34)

由(32)的第二式得xmym=b2，考虑到gcd(xm，ym)=1，有xm=c2，ym=d2，故(c2)2-3d4=1，根据引理7知，c2=1，此时xm=1，则m=0，推出(32)的第一式不成立．

由(33)的第二式得xmym=7b2，考虑到gcd(xm，ym)=1，有

xm=c2，ym=7d2，b=cd，gcd(c，d)=1；

(35)

或

xm=7c2，ym=d2，b=cd，gcd(c，d)=1.

(36)

若(35)成立，则有

c4-3(7d2)2=1.

(37)

由引理8知，方程(37)仅有整数解(c，d)=(±1，0)，此时ym=0，则m=0，推出(33)的第一式不成立．

若(36)成立，则有

(7c2)2-3d4=1.

(38)

由引理7知，方程(38)仅有整数解(c，d)=(±1，±2)，故xm=7，则m=2.此时n=7，所以由(20)，得14qu2=y7+1=2912，即qu2=208，故u=±4，q=13，得v=±2521，所以该情形(18)有整数解(x，u，v)=(4367，±4，±2521)．

由(34)的第二式得xmym=qb2，仿(33)式的讨论知，(18)无整数解．

结合q≡1，3，5(mod 8)或q≡2(mod 3)可得引理10 i)的条件．

完全类似(18)式的讨论知，若q≡3，5，7(mod 8)或q≡2(mod 3)，即引理10 ii)的条件，则(19)无整数解.引理10得证．

引理11i)不定方程组

x+1=7u2，x2-x+1=3v2，gcd(u，v)=1

(39)

仅有整数解(x，u，v)=(-1，0，±1)．

ii)不定方程组

x-1=7u2，x2+x+1=3v2，gcd(u，v)=1

(40)

仅有整数解(x，u，v)=(1，0，±1)．

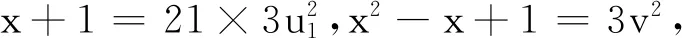
gcd(u，v)=1.

(41)

由引理10知，(41)仅有整数解(x，u1，v)=(-1，0，±1)，从而(39)仅有整数解(x，u，v)=(-1，0，±1).

ii)类似(39)式的讨论知，(40)式仅有整数解(x，u，v)=(1，0，±1).引理11得证.

引理12i)设q为奇素数，且q∈{3，19，43}或q≡1，5，11(mod 12)，则不定方程组

x+1=3u2，x2-x+1=21qv2，

gcd(u，v)=1

(42)

无整数解．

ii)设q为奇素数，且q∈{3，19，31，43，67，73，97}或q≡5，11，13，17，23(mod 24)，则不定方程组

x-1=3u2，x2+x+1=21qv2，gcd(u，v)=1

(43)

无整数解．

证明i)由x=3u2-1≡2，3(mod 4)知，x2-x+1≡3(mod 4)，此时q≡3(mod 4).若q≡1(mod 4)，则(42)无整数解.再根据引理1，若q≡2(mod 3)，则(42)也无整数解.于是q≡1，5，11(mod 12)时，(42)无整数解．

将x=3u2-1代入第二式得3u4-3u2+1=7qv2，即(6u2-3)2-21q(2v)2=-3．

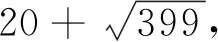
由上式可知，yn为奇数，但yn=2v为偶数，矛盾.故此时(42)无整数解.

ii)由x=3u2+1≡1，4，5(mod 8)知，x2+x+1≡3，5，7(mod 8)，此时21qv2≡5q≡3，5，7(mod 8)，即q≡1，3，7(mod 8).若q≡5(mod 8)，则(43)无整数解.再根据引理1，若q≡2(mod 3)，则(43)也无整数解.于是q≡5，11，13，17，23(mod 24)时，(43)无整数解．

将x=3u2+1代入第二式得3u4+3u2+1=7qv2，即(6u2+3)2-21q(2v)2=-3．

若q=19，则(6u2+3)2-399(2v)2=-3.由i)中q=19的证明知，(43)无整数解．

若q=31，由文献[22]的证明知，(43)无整数解．

若q=43，则(6u2+3)2-903(2v)2=-3.由i)中q=43的证明知，(43)无整数解．

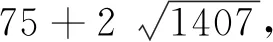
n∈N．

于是6u2+3=±xn.又

xn+2=7502xn+1-xn，x0=75，x1=562725.

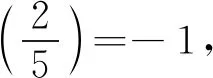
引理13i)设q为奇素数，且q=3或q≡5，11，13，17，19，23，29，31，41，43，47，53，55，59，61，65，67，71，73，83，89，95，97，101，103，107，113，115，125，131，137，139，143，145，149，155，157，163，167 (mod 168)，则不定方程组

x+1=21u2，x2-x+1=3qv2，gcd(u，v)=1

(44)

无整数解．

ii)设q为奇素数，且q∈{3，37}或q≡5，11，13，17，19，23，29，31，41，43，47，53，55，59，61，65，67，71，73，79，83(mod 84)，则不定方程组

x-1=21u2，x2+x+1=3qv2，gcd(u，v)=1

(45)

无整数解．

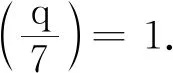
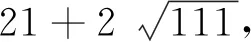
于是42u2+3=±xn.又

xn+2=590xn+1-xn，x0=21，x1=12411.

对上式取模7，有xn≡0(mod 7).由此知3≡0(mod 7)，不可能.故此时(45)无整数解.下证其他情形．

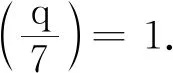
引理14i)设q为奇素数，且q≡1，3，5，9，11，13，15，17，19，23，25，27，29，33，37，39，41，43，45，51，53(mod 56)，则不定方程组

x+1=3qu2，x2-x+1=21v2，gcd(u，v)=1

(46)

无整数解．

ii)设q为奇素数，且q≡3，5，11，13，15，17，19，23，27，29，31，33，37，39，41，43，45，47，51，53，55(mod 56)，则不定方程组

x-1=3qu2，x2+x+1=21v2，gcd(u，v)=1

(47)

无整数解．

证明i)将(46)的第一式代入第二式得

(6qu2-3)2-21(2v)2=-3.

(48)

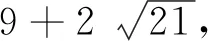
因此根据(48)有

6qu2-3=±xn.

(49)

容易验证下式成立：

xn+2=110xn+1-xn，x0=9，x1=999.

(50)

对递归序列(50)取模16得剩余类序列的周期为2：9，7，9，7，…，且n≡0(mod 2)时，xn≡9(mod 16)；n≡1(mod 2)时，xn≡7(mod 16).此时(49)式成为 6qu2-3≡±9，±7(mod 16)，即qu2≡2，7(mod 8)，进一步讨论知仅当q≡7(mod 8)时才可能成立.若q≡1，3，5(mod 8)，则(46)无整数解.

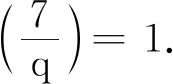
结合q≡1，3，5(mod 8)或q≡5，11，13，15，17，23(mod 28)可得引理14 i)的条件．

ii)完全类似(46)式的讨论知，若q≡3，5，7(mod 8)或q≡5，11，13，15，17，23(mod 28)，即引理14 ii)的条件，则(47)式无整数解.引理14得证．

2 定理的证明

先证定理1．

因为gcd(x+1，x2-x+1)=1或3，故方程(2)给出以下8种可能的分解.

Ⅰx+1=7qu2，x2-x+1=v2，y=uv，gcd(u，v)=1；

Ⅱx+1=u2，x2-x+1=7qv2，y=uv，gcd(u，v)=1；

Ⅲx+1=7u2，x2-x+1=qv2，y=uv，gcd(u，v)=1；

Ⅳx+1=qu2，x2-x+1=7v2，y=uv，gcd(u，v)=1；

Ⅴx+1=21qu2，x2-x+1=3v2，y=3uv，gcd(u，v)=1；

Ⅵx+1=3u2，x2-x+1=21qv2，y=3uv，gcd(u，v)=1；

Ⅶx+1=21u2，x2-x+1=3qv2，y=3uv，gcd(u，v)=1；

Ⅷx+1=3qu2，x2-x+1=21v2，y=3uv，gcd(u，v)=1．

以下讨论这8种情形所给的方程(2)的整数解.

对于情形Ⅰ，解第二式，得x=0，1，均不适合第一式，故该情形方程(2)无整数解．

对于情形Ⅱ，由引理3 i)知，该情形方程(2)无满足条件的整数解．

对于情形Ⅲ，由引理4 i)和引理11 i)知，该情形方程(2)无满足条件的整数解．

对于情形Ⅳ，由引理5 i)知，该情形方程(2)无满足条件的整数解．

对于情形Ⅴ，由引理10 i)知，该情形方程(2)满足条件的整数解仅有(x，y)=(-1，0)．

对于情形Ⅵ，由引理12 i)知，该情形方程(2)无满足条件的整数解．

对于情形Ⅶ，由引理13 i)知，该情形方程(2)无满足条件的整数解．

对于情形Ⅷ，由引理14 i)知，该情形方程(2)无满足条件的整数解.

综上，定理1得证．

再证定理2．

因为gcd(x-1，x2+x+1)=1或3，故方程(3)给出以下8种可能的分解.

Ⅰx-1=7qu2，x2+x+1=v2，y=uv，gcd(u，v)=1；

Ⅱx-1=u2，x2+x+1=7qv2，y=uv，gcd(u，v)=1；

Ⅲx-1=7u2，x2+x+1=qv2，y=uv，gcd(u，v)=1；

Ⅳx-1=qu2，x2+x+1=7v2，y=uv，gcd(u，v)=1；

Ⅴx-1=21qu2，x2+x+1=3v2，y=3uv，gcd(u，v)=1；

Ⅵx-1=3u2，x2+x+1=21qv2，y=3uv，gcd(u，v)=1；

Ⅶx-1=21u2，x2+x+1=3qv2，y=3uv，gcd(u，v)=1；

Ⅷx-1=3qu2，x2+x+1=21v2，y=3uv，gcd(u，v)=1．

以下讨论这8种情形所给的方程(3)的整数解．

对于情形Ⅰ，解第二式，得x=0，-1，均不适合第一式，故该情形方程(3)无整数解．

对于情形Ⅱ，由引理3 ii)知，该情形方程(3)无满足条件的整数解．

对于情形Ⅲ，由引理4 ii)和引理11 ii)知，该情形方程(3)无满足条件的整数解．

对于情形Ⅳ，由引理5 ii)知，该情形方程(3)无满足条件的整数解．

对于情形Ⅴ，由引理10 ii)知，该情形方程(3)满足条件的整数解仅有(x，y)=(1，0)．

对于情形Ⅵ，由引理12 ii)知，该情形方程(3)无满足条件的整数解．

对于情形Ⅶ，由引理13 ii)知，该情形方程(3)无满足条件的整数解．

对于情形Ⅷ，由引理14 ii)知，该情形方程(3)无满足条件的整数解．

综上，定理2得证．

3 推论的证明

先证推论1．

当q=11，23，29，53，71时，由定理1直接可得方程(2)仅有整数解(x，y)=(-1，0)．

当q=3，5，13，17，19，41，43，59，61，73，83，89，97时，对于情形Ⅰ，方程(2)均无整数解；对于情形Ⅱ，由引理3 i)知，方程(2)均无整数解；对于情形Ⅲ，由引理4 i)和引理11 i)知，方程(2)除开q=3时仅有整数解(x，y)=(-1，0)外，其他情况均无整数解；对于情形Ⅳ，由引理5 i)知，方程(2)除开q=5仅有整数解(x，y)=(19，±14)外，其他情况均无整数解；对于情形Ⅴ，由引理10 i)知，方程(2)除开q=13仅有整数解(x，y)=(-1，0)和(4367，±30252)外，其他情况仅有整数解(x，y)=(-1，0)；对于情形Ⅵ，由引理12 i)知，方程(2)均无整数解；对于情形Ⅶ，由引理13 i)知，方程(2)均无整数解；对于情形Ⅷ，由引理14 i)知，方程(2)均无整数解.推论1得证.

说明1对于100以内的奇素数q，仍遗留q=31，37，47，67，79，有待解决．

再证推论2．

当q=11，23，29，53，71时，由定理2直接可得方程(3)仅有整数解(x，y)=(1，0)．

当q=3，5，13，17，19，31，37，41，43，59，61，67，83，89时，对于情形Ⅰ，方程(3)均无整数解；对于情形Ⅱ，由引理3 ii)知，方程(3)均无整数解；对于情形Ⅲ，由引理4 ii)和引理11 ii)知，方程(3)除开q=3时仅有整数解(x，y)=(1，0)外，其他情况均无整数解；对于情形Ⅳ，由引理5 ii)知，除开q=17时方程(3)仅有整数解(x，y)=(18，±7)外，其他情况均无整数解；对于情形Ⅴ，由引理10 ii)知，方程(3)均仅有整数解(x，y)=(1，0)；对于情形Ⅵ，由引理12 ii)知，方程(3)均无整数解；对于情形Ⅶ，由引理13 ii)知，方程(3)均无整数解；对于情形Ⅷ，由引理14 ii)知，方程(3)均无整数解.推论2得证.

说明2对于100以内的奇素数q，仍遗留q=47，73，79，97，有待解决．