截断肋排布方式对内冷通道换热性能的影响

张国花，谢公南，SUNDÉN Bengt，李书磊

（1.西北工业大学机电学院，西安 710072；2.西北工业大学航海学院，西安 710072；3.隆德大学能源科学系，隆德SE⁃ 22100；4.西北工业大学深圳研究院，深圳 518057）

内部对流冷却是燃气涡轮设计中最早应用的冷却技术[1⁃2]。肋片冷却[3⁃5]是内部冷却的主要方式之一，肋片的几何特征、布置方式对内冷通道的流动传热特性有一定的影响。在兼顾冷却通道压力损失的前提下，设计新型高效的肋片冷却结构以更有效地降低涡轮叶片表面温度、延长叶片工作时间势在必行。

相较于连续直肋，截断肋因能减小通道压力损失而被广泛研究[6⁃7]。Li 等[6]的研究表明截断肋通道的压力损失比连续肋小，但是其换热增强作用稍弱于连续肋。Singh 等[7]的研究表明多处横向截断肋通道的压力损失减小而且换热亦得到强化。Zhang 等[8]基 于 构 形 理 论[9⁃10]提 出 了 构 形 截 断 肋，实验与数值研究，发现构形截断肋提高通道换热的同时减小通道压降。此外，为减小肋片通道的压力损失，Li 等[11]提出了带条缝的肋片，结果表明，小高度肋上的条缝有利于减小通道压降而大高度肋上的短条缝有利于增强通道换热。对倾斜肋上开矩形孔或圆孔的研究表明[12]，带有倾斜角的矩形孔或圆孔有利于减小通道的压力损失。邓贺方等[13]提出了狭缝斜肋，数值研究发现狭缝的存在显著改变了通道内的流动结构与换热分布、降低了通道压力损失并强化了肋片表面的换热。另外，肋片结合其他强化单元结构亦是一种新的内冷方式。Chom⁃pookham 等[14]通过在楔形肋通道入口布置三角翼达到强化换热的效果。Zheng 等[15]研究了肋片⁃凹槽⁃凸起的不同组合对通道换热性能的影响。张峰等[16]研究了肋片与凹槽共同作用下通道的流动换热特性，结果显示，展向分布不均匀的肋片产生的旋转涡对有利于带走凹槽内的低速热空气从而强化换热。

本文在前期研究基础上[8]，研究构形截断肋通道中4 排截断肋片6 种不同排布方式下的流动换热特性。通过实验研究的方法，在固定通道雷诺数的条件下，对构形截断肋的不同排布方式下的换热性能进行测试研究，并结合计算流体力学方法，深入探究并分析其中的流动换热机理，为含截断肋的燃气涡轮高效冷却结构设计提供参考。

1 实验过程

1.1 实验设置

实验系统如图1 所示，其中矩形通道的长、宽和高分别为500、32 和8 cm。为减小通道的导热损失，通道材料选取导热率较小（0.2 W/（m·K））的有机玻璃。通道内主流由固定于通道右端的离心风机提供，通道入口设计为钟形，使空气顺利进入通道。为确保实验过程中流体的充分发展特性，长为50 cm 的测试段放置于通道下游处。加热箔粘贴在测试段通道表面以提供均匀热流，加热箔厚度小于1 mm，由铜⁃镍合金制成，加热箔连接电流表及交流电压控制器以改变加热箔两端电压。稳态液晶膜R35C5W 贴于加热箔上方。此外，为减小测试段的导热损失，测试段背面固定一块导热率仅为0.03 W/（m·K）的绝热 泡沫。实验中，分辨率为1 600 像素×1 200 像素的CCD 相机垂直地设置在测试段上方以捕捉液晶膜的图片，同时，在测试段上游和下游分别设置测压孔，由压力计测量测试段处的压力损失。整个测试段采用不透光的黑布进行遮盖，以减小周围自然光对实验结果的影响。

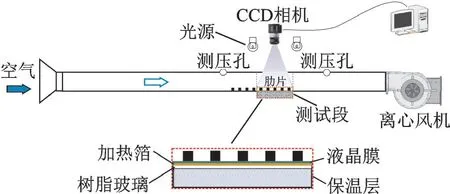
图1 实验系统示意图Fig.1 Illustration of experimental system

为表述方便，本文模型根据一个周期内4 排截断肋片中每排截断肋片的个数为命名规则。如图2(a)所 示，6 个 模 型 分 别 命 名 为 结 构2⁃3⁃5⁃9、结 构2⁃3⁃9⁃5、结构2⁃5⁃3⁃9、结构2⁃5⁃9⁃3、结构2⁃9⁃3⁃5 和结构2⁃9⁃5⁃3。通道中共布置9 排截断肋，第1 排至第4 排为一个周期，放置于测试段上游，以达到流体充分发展的目的；第5 排至第8 排为第二个周期，放置于测试段，测试段后端布置第9 排肋片，作为一个完整周期截断肋的换热测试区。图中，结构2⁃3⁃5⁃9 中 一 个 周 期 内 的 截 断 肋 片 以 构 形 方 式 排列，因此结构2⁃3⁃5⁃9 中肋片截断型式称之为构形截断肋[8]。图2(b)给出了截断肋的具体尺寸，肋宽为1 cm，肋高为1 cm（即为正方形截面肋），肋间距为10 cm，每排肋片总长度均为24 cm（截断长度总和均为8 cm）。本文主要目的是探究一个周期内4排截断肋片6 种不同排布方式下内冷通道的换热特性及其机理。

图2 不同内冷结构示意图Fig.2 Illustration of different internal cooling structures

1.2 液晶热像校准及实验数据处理

对采集到的液晶图片进行处理，得到测试段通道壁面的温度和壁面换热系数，液晶的具体校准过程及校准结果参见文献[8]。

实验过程中通道入口平均速度u0通过以下公式获得

式中：umax和u*分别为通道中心最大速度和摩擦速度。通道最大速度umax通过Testo⁃416 风速计测得，摩擦速度u*通过Moody 表[17]中给出的摩擦因子计算得到。

通道雷诺数定义如下

式中：ρ、μ和Dh分别为空气的密度、动力黏度以及通道的水力直径。

壁面对流换热系数定义为

式中：qw和qloss分别为测试段壁面施加的热流密度以及测试段的热损失。壁面温度Tw通过对液晶图片进行处理得到，流体参考温度Tf由以下公式给出

式中：Tin为通道入口流体温度，由温度计测得；Q、Lheated和cp分别为测试段的加热功率、测试段长度和空气的比热容；H和W分别为通道的高度和宽度。

壁面努塞尔数定义为

式中λ为空气的导热系数。

范宁摩擦因数定义为

式中：Δp为两测压孔间的压降，L为两测压孔的距离。本 文 将 选 取Dittus⁃Boelter 公 式 和Blasius 公式[18⁃19]对努塞尔数和摩擦因数进行无量纲化。

实验误差由文献[20]中的方法计算得到。基于实验过程中电流与电压的误差，计算得到热流密度的误差约为4%。实验中，空气入口温度与壁面温度的测量误差分别为0.1 和±0.2 K。导热损失与辐射损失的误差小于6%。因此，计算得到换热系数与努塞尔数的误差均为±6%。此外，摩擦因数的计算误差与压降的测量误差分别为5%和3%。

2 计算模型及方法

2.1 计算域及边界条件

模型的高、宽、长以及截断肋在的排布方式均与前述实验模型（图2）保持一致。为提高计算稳定性，通道的入口向上游延伸60 cm，出口向下游延伸40 cm，即入口段与出口段的长度分别为100 和40 cm。边界条件与实验工况保持一致，通道入口给定10 m/s 的均匀速度（即流体雷诺数为80 000），湍流强度为5%，入口温度为300 K；通道出口边界采用压力出口；测试段底部壁面施加1 000 W/m2的均匀热流密度，其余壁面均为无滑移绝热条件。

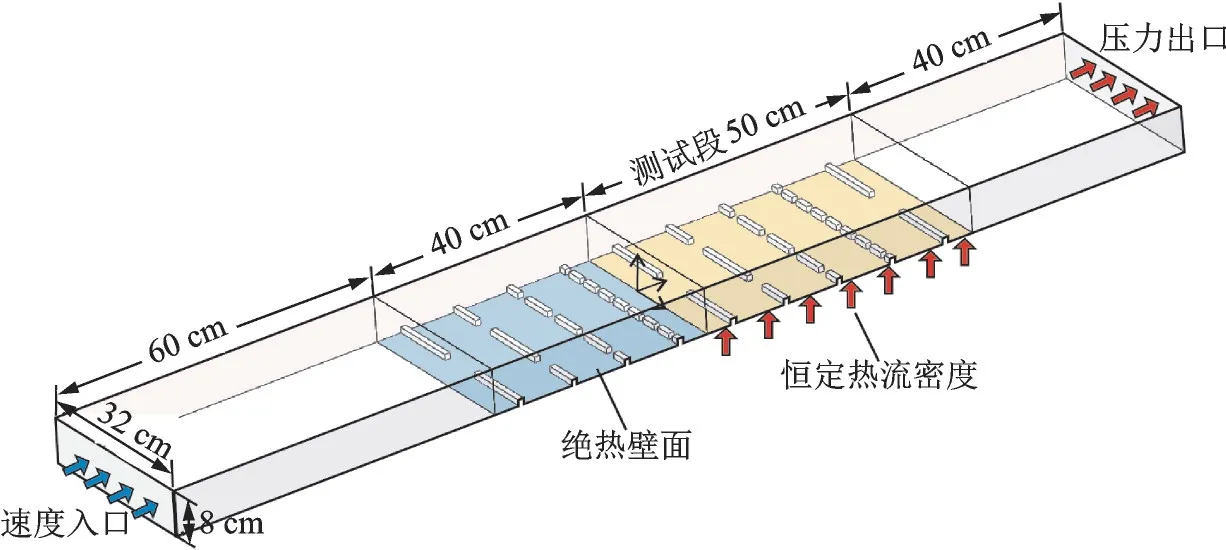
图3 计算模型及边界条件Fig.3 Computational model and boundary conditions

2.2 网格及独立性验证

采用商用软件ANSYS ICEM CFD 17.2 对计算域进行结构化网格划分，且加密近壁面网格以确保y+值小于1，如图4(a)所示。基于结构2⁃3⁃5⁃9，对4 种不同网格数（500 万、600 万、710 万和820 万个）进行网格独立性验证，比较测试段表面的面平均努塞尔数。由图4(b)可见，相较于500 万和600万个的网格密度，710 万与820 万个网格密度下的面平均努塞尔数更为接近，偏差更小。因此，为缩减计算量并保证计算精度，本文选用网格数为710万个对结构2⁃3⁃5⁃9 进行数值计算，并以相同网格划分策略对其余5 种结构生成相近网格数的结构化网格。

图4 结构2⁃3⁃5⁃9 的网格划分及独立性验证结果Fig.4 Mesh adopted in simulations and mesh indepen⁃dent test for Case 2⁃3⁃5⁃9

2.3 湍流模型验证

为验证本文的数值模型，以结构2⁃3⁃5⁃9 的实验数据为基础，比较不同湍流模型下计算得到的测试段表面无量纲努塞尔数及其展向平均值。由图5 可看出，基于湍流模型Transitionk‑kl‑ω得到的努塞尔数分布与实验观测的分布吻合较好；此外，从沿程展向平均努塞尔数分布来看，相比其他湍流模型，Transitionk‑kl‑ω模型下的数值结果及趋势与实验结果最为接近。因此，本文采用Transitionk‑kl‑ω湍 流 模 型 对6 种 结 构 进 行 流 动 传 热 数 值计算。

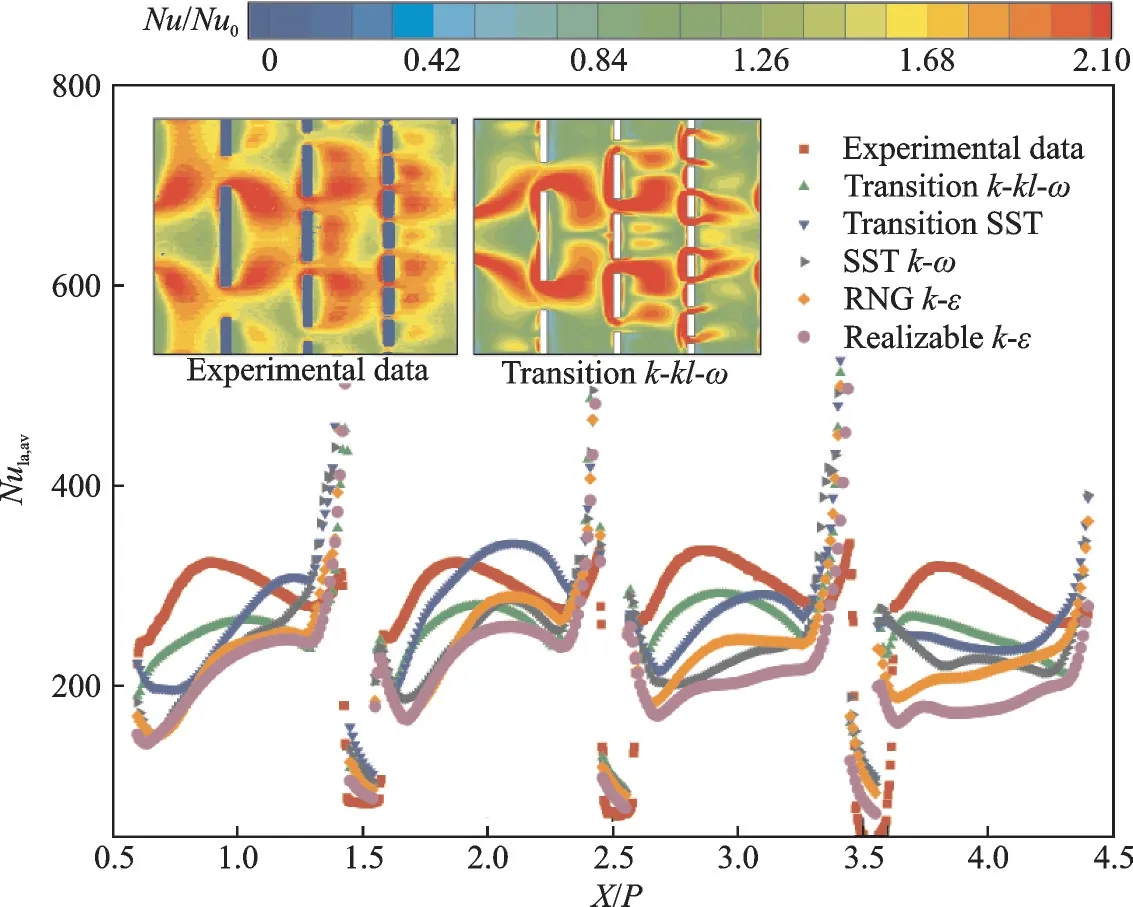
图5 比较结构2⁃3⁃5⁃9 实验和数值模拟结果中通道底面的努塞尔数云图及展向平均分布图Fig.5 Validation of numerical model by comparing the Nusselt number contours and laterally averaged Nusselt number on the bottom wall of the test section for experimental and numerical results for Case 2⁃3⁃5⁃9

2.4 数值方法

基于有限体积法的商业软件FLUENT 17.2进行三维稳态求解，压力⁃速度耦合采用SIMPLEC算法，控制方程中对流项用二阶迎风格式进行离散。解收敛标准为各项残差的精度均小于10-5且残差曲线趋于平缓及测试段表面的努塞尔数保持不变。由于通道入口与出口处流体的温度相差不大，因此，计算工质选取为不可压理想气体。

3 结果与讨论

3.1 内冷通道中测试段不同结构的换热性能

图6 为实验得到的6 种不同结构的努塞尔数分布云图。由图可见，同一排截断肋片放置于通道的不同位置，局部的换热特征明显不同，例如，9 个小肋片构成的一排截断肋放置于测试段的第2 排时（结构2⁃9⁃5⁃3），其肋后的换热效果优于将该排肋片放置于测试段第4 排时（结构2⁃5⁃3⁃9）的换热效果；即使6 种结构中第1 排肋片均由两个截断肋构成，且在测试段上游放置了与测试段相同的截断肋片（一个周期），流体在测试段内产生不同的流动特征，导致第2 排截断肋下游的换热特征也有差别。此外，截断肋通道中高努塞尔数区域位于截断肋下游，而肋后及肋片截断区域的努塞尔数较低。由于截断肋片结构在通道中的对称性布置，测试段表面的努塞尔数也呈对称分布。

为定量比较不同结构下肋片下游的换热特性，图7 给出与图6 中努塞尔数云图对应的展向平均努塞尔数分布。可见，在相邻两排截断肋中间，换热效果先增加后降低，再增加。当0.55＜X/P＜1.45 时，结构2⁃9⁃5⁃3 的换热效果最好，结构2⁃9⁃3⁃5的换热效果次之，结构2⁃3⁃9⁃5 和结构2⁃5⁃3⁃9 的换热效果最差；当1.55 ＜X/P＜2.45 时，结构2⁃9⁃5⁃3在上游肋后的换热效果最好，结构2⁃9⁃3⁃5 在下游肋前的换热效果最差；当2.55 ＜X/P＜3.45 时，结构2⁃3⁃5⁃9 的换热效果最好。此外，沿流向方向，结构2⁃9⁃5⁃3 和结构2⁃5⁃9⁃3 的换热效果逐渐降低，而结 构2⁃3⁃5⁃9 和 结 构2⁃3⁃9⁃5 在2.55 ＜X/P＜3.45时换热效果最好。

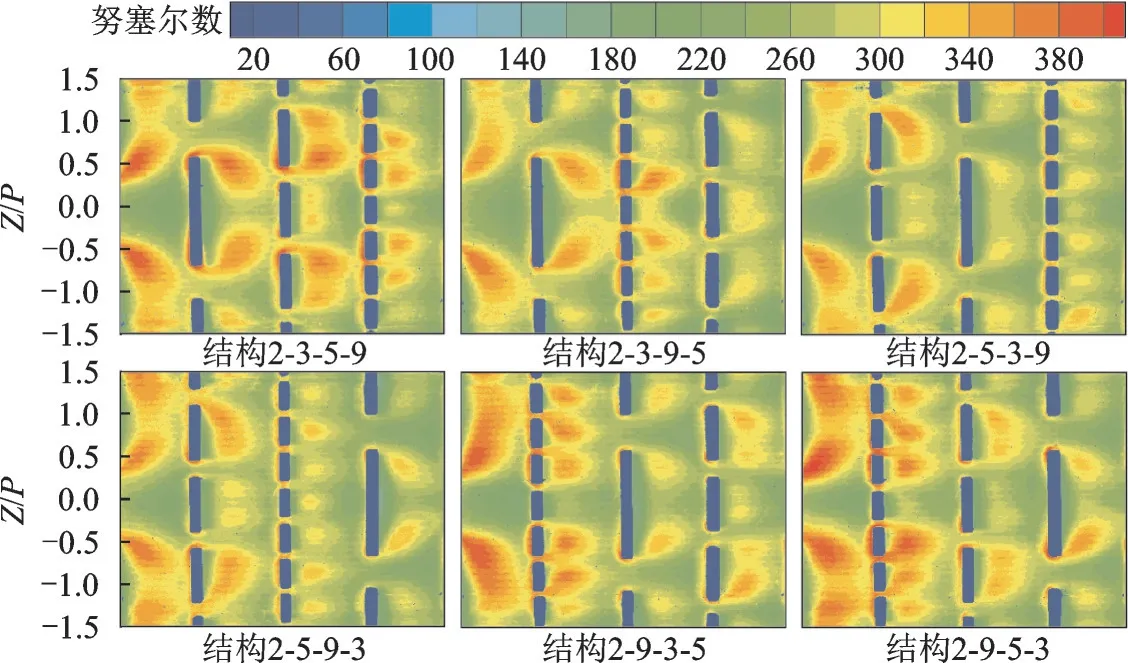
图6 实验得到的不同结构测试段表面努塞尔数分布云图Fig.6 Nusselt number distribution contours for considered six cases by LCT experiment

图7 比较图6 中不同结构的努塞尔数云图对应的努塞尔数展向平均分布Fig.7 Comparisons of laterally⁃averaged Nusselt number distributions corresponding to the contours shown in Fig.6 for different structures

表1 对比了不同结构的无量纲面平均努塞尔数、摩擦因数及总体热性能。结构2⁃3⁃5⁃9 的换热性 能 最 好，结 构2⁃9⁃5⁃3 的 换 热 性 能 次 之，而 结 构2⁃5⁃3⁃9 的换热性能最差，其中结构2⁃3⁃5⁃9 比结构2⁃9⁃5⁃3 的换热性能高0.4%，比结构2⁃5⁃3⁃9 的换热性能高4.8%。然而，就摩擦因数而言，结构2⁃3⁃5⁃9 的 最 大，结 构2⁃9⁃5⁃3 的 次 之，结 构2⁃5⁃9⁃3的最小；与结构2⁃3⁃5⁃9 相比，结构2⁃5⁃9⁃3 的摩擦因数 减 小 了6.5%，结 构2⁃9⁃5⁃3 的 摩 擦 因 数 减 小 了1.6%。从总体热性能来看，结构2⁃9⁃5⁃3 的最高，结构2⁃5⁃3⁃9 的最低，且前者的总体热性能比后者2⁃5⁃3⁃9 的高2.9%。总的来说，4 排截断肋片在内冷通道的不同排布方式对通道的换热性能及总体热性能有一定的影响，但相差不大。

表1 比较内冷通道中不同结构的无量纲面平均努塞尔数及摩擦因数Table 1 Comparisons of dimensionless area averaged Nusselt number and friction factor of considered structures in in⁃ternal cooling channel

3.2 不同内冷结构通道中流体的流动特征

为明晰截断肋片不同排布方式下的流动换热机理，图8 展示了数值计算得到的通道底面流线及法向位置y= 0.003 mm 上的截面速度分布。由流线图可见，由于肋片对流体的阻碍作用，每条肋片的后方都存在一个回流区，该区域流体的换热效果较差；截断区域的存在以及肋后的负压梯度，使流体在截断肋后方形成一对反向旋转的横向涡对，使得流体被明显扰动，增强主流流体与边界层内流体的掺混，通道的换热性能明显提高，这在图6 中局部努塞尔数分布得到印证。此外，由于截断区域的存在，流体对下游肋片前侧产生强烈的剪切力，有效地减小肋片前侧的流动边界层，增强对肋片附近流体的扰动，强化了换热。对于6 种不同的内冷结构，由于4 排截断肋片排布方式的差异，每排肋片前侧流体的流动特征不同，流体所受剪切力不同，换热效果也因而不同。由速度分布图可见，流体在截断区域均呈现不同程度的加速，且位于通道中间的截断区域，流体加速更加明显，这一现象增强主流流体和边界层内流体的掺混，进而强化换热。因此，截断肋的不同排布方式下流体的流动特征不尽相同。

图9 展示了上述截面的湍流动能分布。湍流动能是湍流强度的度量，肋片截断区域诱导的横向涡、反向旋转涡对等二次流的产生与发展有力地促进了流体间的碰撞和掺混，使流体具有高湍流动能。湍流动能越高，流体间的碰撞和掺混越剧烈，换热性能越好。由图可见，不同结构的高湍流动能区域出现在截断肋片下游，与截断区域诱导的横向涡位置相同，结合图6 中局部努塞尔数分布特征（高努塞尔数区域与高湍流动能区域对应），进一步表明高湍流动能有利于加强流体的掺混，增强流体间能量交换，换热得到强化。

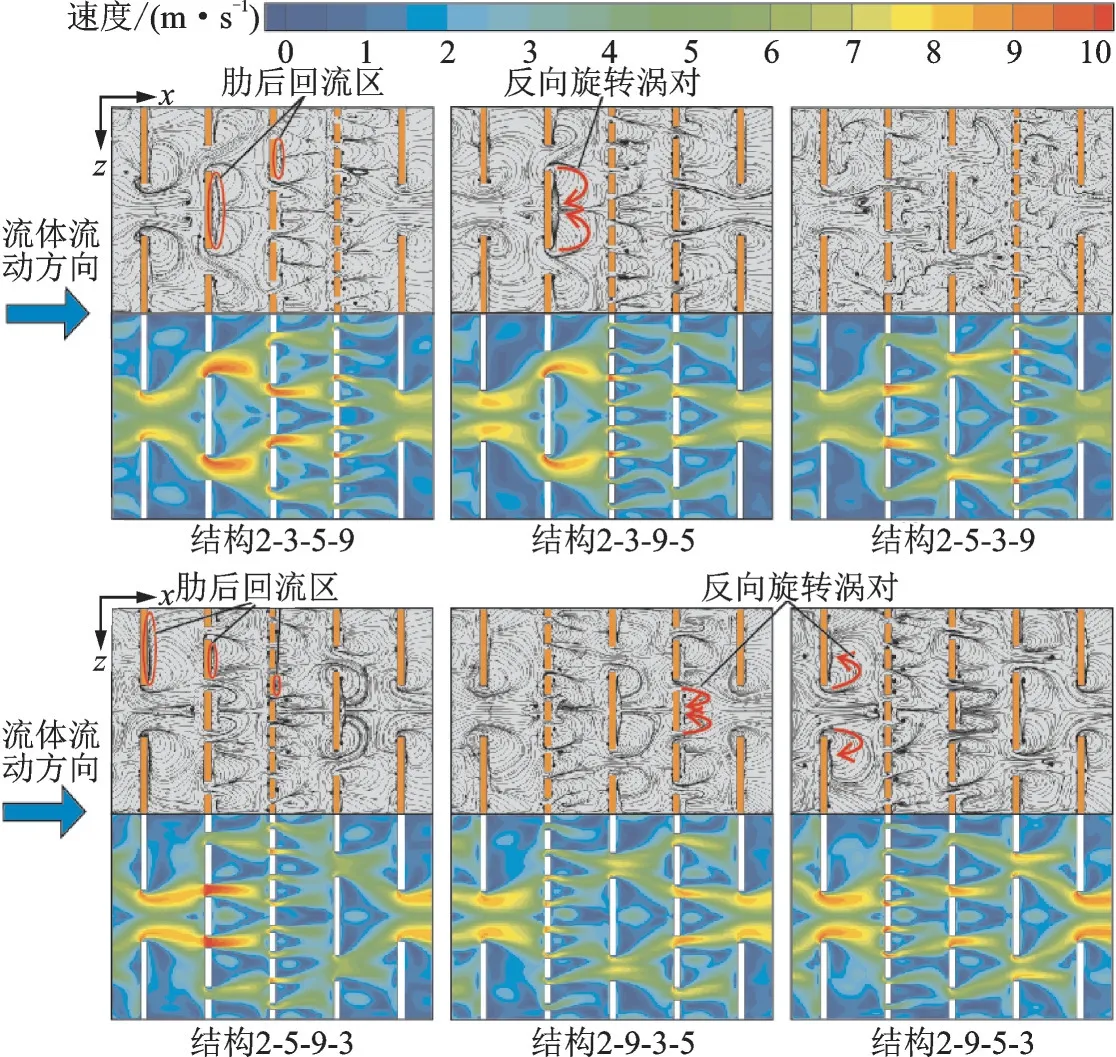
图8 测试段底面不同结构的流线图以及y = 0.003 mm 的x‑z 平面上流体的速度分布云图比较Fig.8 Surface streamline on the bottom wall and velocity magnitude contours on a x‑z plane at y = 0.003 mm of test sec⁃tion for considered structures

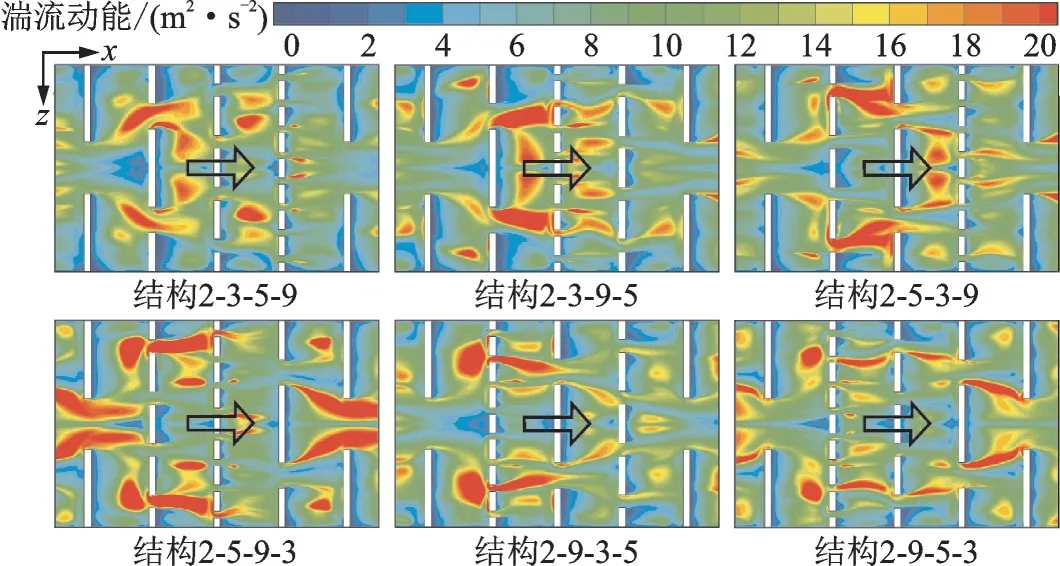
图9 测试段不同结构在y = 0.003 mm 的x‑z 平面上的湍流动能分布云图Fig.9 Local turbulence kinetic energy distributions on a x‑z plane at y = 0.003 mm of test section for considered cases

为了更好地理解不同排布方式下的流动特性，图10 给出了6 种结构的压力系数分布云图。压力系数的定义为

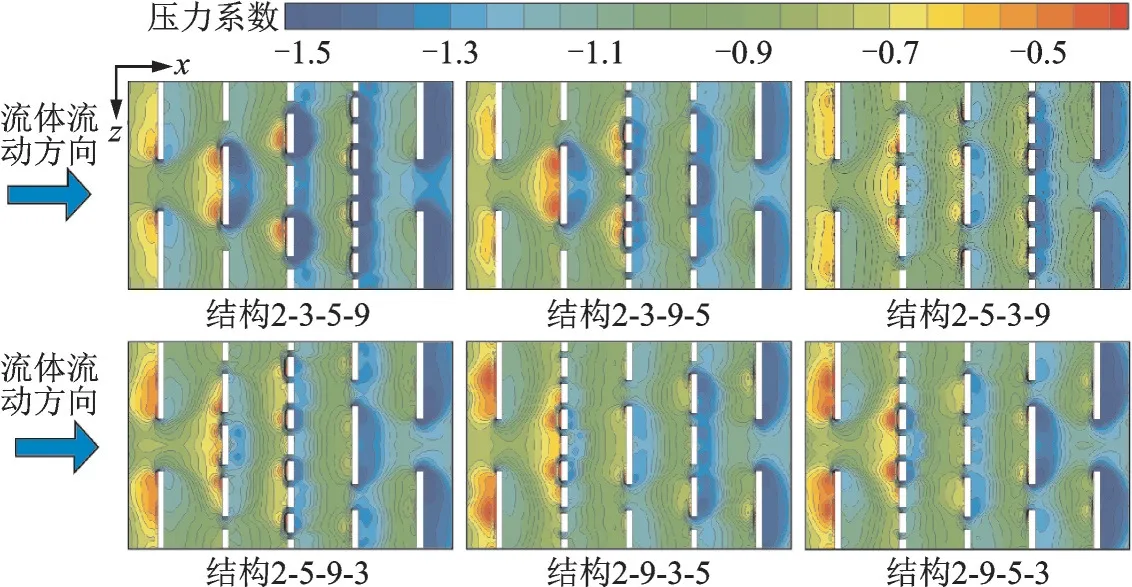
图10 测试段底面不同结构的压力系数分布云图Fig.10 Pressure coefficient distributions on the bottom wall of test section for considered cases

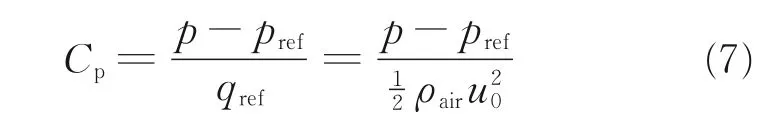
式中：pref为通道入口压力，qref为通道入口动压。由图可见，通道中低压力系数区域位于截断肋后回流区，该区域流体湍流动能小、换热差；高压力系数区域位于截断肋前侧冲击区以及相邻两排肋片间流体的再附着区，由于肋片前后压力梯度的作用，流体绕过截断区域，在肋后形成横向涡。此外，由图可知，即使每排截断肋肋片个数相等，由于4 排截断肋片排布方式的差异，肋后压力系数分布也有所差异，这与图8 中流动特征相对应。在6 种排布方式中，结构2⁃3⁃5⁃9 的压力损失最大。

图11 展示了不同结构通道中沿程4 个截面（X/P= 1，X/P=2，X/P=3 和X/P=4）上的流线及湍流动能分布。由图可知，由于截断肋片对流体的阻碍作用，每个截面上的高湍流动能区域并不连续，这些区域位于通道底面附近，并位于截断肋下游。相对于肋片下游的湍流动能，肋片截断区域下游的湍流动能较低，靠近通道两侧的湍流动能也较低，通道中上方的湍流动能最低。从截面上流线图可见，不同结构的4 个截面中间均有一对向外的反向旋转涡对，但反向旋转涡对对通道底面的冲击区域不同，这些被冲击的区域均为高湍流动能区域。这一现象与上述高湍流动能区域的流体混合及碰撞剧烈这一结论相吻合。

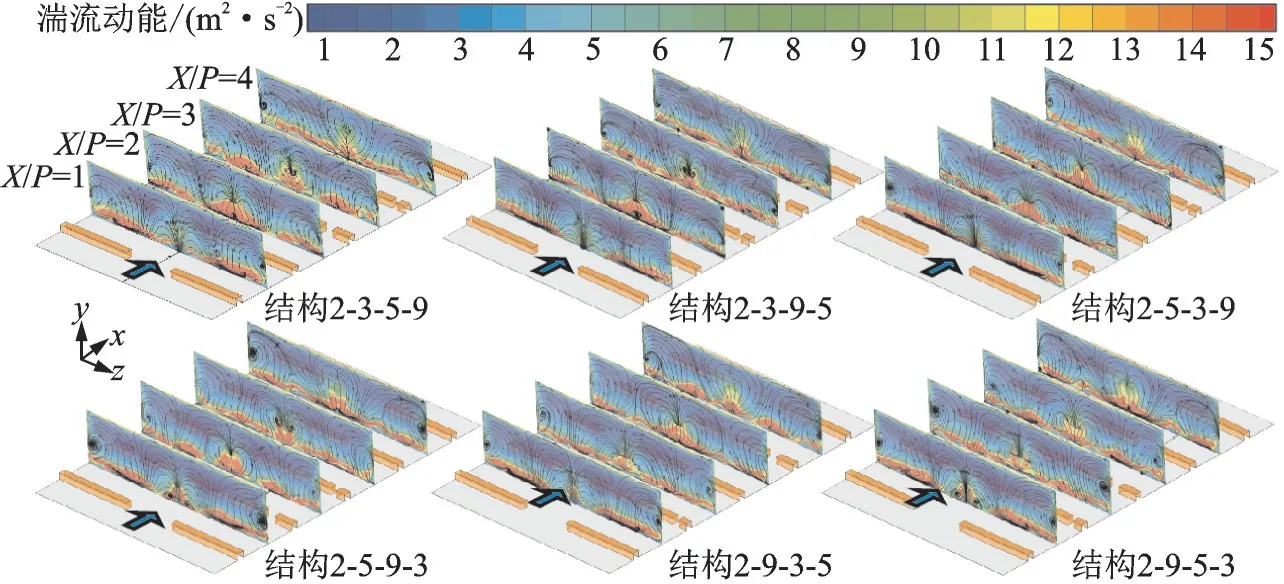
图11 不同内冷结构通道中4 个y‑z 截面上的流线图及湍流动能分布图，4 个y‑z 截面分别为X/P=1，2，3 和4 Fig.11 Streamline and TKE distributions on four y‑z planes, i.e., X/P=1，2，3 and 4 for the considered cases

4 结 论

本文通过实验结合数值模拟的方法，在给定内冷通道雷诺数的条件下，研究了构形截断肋中4 排截断肋片的6 种不同排布方式下的换热特性和流动换热机理，得到以下结论：

（1）在6 种排布方式中，结构2⁃3⁃5⁃9 的换热性能最好，结构2⁃9⁃5⁃3 的换热性能次之，结构2⁃5⁃3⁃9的换热性能最差；结构2⁃3⁃5⁃9 通道的压力损失最大，结构2⁃9⁃5⁃3 通道的压力损失次之，结构2⁃5⁃9⁃3通道的压力损失最小；结构2⁃9⁃5⁃3 的总体热性能最好，结构2⁃3⁃5⁃9 的次之，结构2⁃5⁃3⁃9 的总体热性能最差。

（2）截断区域的存在使得肋片后方产生负压梯度，肋后形成一对反向旋转的横向涡，对流体产生剧烈扰动，通道中主流流体与边界层内流体的掺混得到增强；截断肋的不同排布方式下流体的流动特征不同，但其在截断区域所诱导的涡结构相似。