考虑模糊参数的DG配电网静态电压稳定指标研究
周惠芳
(湖南电气职业技术学院,湖南 湘潭 411101)
0 引 言
当今世界,对能源的需求不断增强,世界各国充分利用风能、太阳能、水力和天然气等多种能源进行发电。分布式电源技术(distributed generation,DG)迅速发展,分布式电源并入配电网后,配电网的管理和控制变得更加复杂,给配电网的电压、潮流、电能质量、规划和稳定运行带来一系列的问题。分布式发电与集中式发电的有效结合成为未来发电方式的主流,这就要求进一步研究分布式电源接入对配电网静态电压稳定性的影响,为分布式电源的配置、并网运行和规划提供参考[1]。
文献[2]在对DG建模时将其节点类型分为两类:一类为小容量的DG,该类DG并不一定会参与电压调节,可以认为是PQ节点;另一类为通过逆变器并网的DG,该类DG可以控制无功输出,为PV节点,并提出了一种基于网损灵敏度的潮流算法。文献[3]从定量的角度研究了不同类型DG对配电系统电压稳定的影响。本文研究的主要内容:在基于已有DG接入配电网对静态电压稳定性影响的基础上,考虑DG出力模糊性和负荷接入量模糊化等因素,通过对异步发电机并网模型简化,构建反应异步风机并网后节点电压变化的静态电压稳定指标,并进行随机模糊潮流计算。从P-Q(V)型DG并网容量、接入位置及无功补偿等方面,考虑确定参数下和随机模糊参数下DG接入对配电网静态电压稳定性的影响。
1 考虑模糊参数的DG系统状态样本抽样和随机潮流问题求解步骤

图1 异步风力发电随机潮流问题求解步骤
本文以异步风力发电机并网为例。考虑风电出力的随机性,文献[4]认为风速用Weibull分布双参数曲线描述,提出负荷采用正态分布描述其随机性,且两者之间彼此相互独立,采用蒙特卡罗法(monte carlo method, MC)随机模拟获取风电出力和负荷样本。再利用MC和前推回代法对随机潮流问题求解,量化传统模型中确定性静态安全参数,如支路潮流、节点电压和禁止倒送功率的概率约束[5]。步骤如图1所示。
节点电压、支路功率正常的概率及功率不倒送的概率计算公式见文献[6]。
2 P-Q(V)节点在配网潮流计算中的处理
异步发电机在并网中归属于P-Q(V)型节点,进行潮流计算时需将其处理成PQ节点。
2.1 异步发电机参数求取
当今我国异步风力发电机应用比较广泛。异步发电机本身没有励磁系统,只有靠从电网中吸收无功来建立磁场,而其吸收的无功又受其机端电压的约束,因此不能简单将其视为一般的PQ、PV节点,需采用更详细的计算模型[7],异步发电机的等效电路模型见图2(a)。因其励磁靠无功形成,且励磁电阻Rm远小于励磁电抗Xm,定子电阻Rs远小于定子电抗Xs,故简化计算时近似忽略Rm和Rs;励磁电抗远大于定子电抗,故将励磁支路移至电路首端,得到简化的电路模型见图2(b)。

图2 异步发电机等效电路
图2中:Rs为定子电阻;Xs为定子电抗;Rm为励磁电阻;Xm为励磁电抗;Rr为转子电阻;Xr为转子电抗;Rr(1-s)/s为风机输入机械功率的等效电阻。Rr/s=Rr+Rr(1-s)/s。
式(1)~式(3)分别是异步发电机有功功率P、转差率s和无功功率Q的求取公式。
(1)
(2)
(3)
一般情况下视异步风力发电机的风速恒定,则有功功率P恒定,每次迭代中节点电压U是变化的,根据有功P和转差率s求取无功Q。将转差率s代入式(3)得:
(4)
由式(4)得到无功Q与机端电压U之间的关系。无功功率随机端电压的变化而变化。
2.2 潮流计算中P-Q(V)节点的处理方法
异步风力发电机,在实际并网运行中,其本身不具备并网电压调节能力,需从电网吸收无功功率建立磁场。为减少网络损耗,提高运行可靠性,该类发电机都装设有并联电容器组成的无功补偿装置,用以保证其功率因数在允许变动范围内,功率因数cosφ与并联电容器所提供的无功功率可按照式(5)~式(8)确定。
(5)
式中:PG为异步发电机发出的有功功率;QC为补偿装置在并联电容器电压等级下提供的无功功率;Q′为异步发电机吸收的无功功率。为使异步发电机功率因数由原来的cosφ1提升到cosφ2,计算并联电容器组提供的无功功率如式(6)所示。
(6)
一般并联电容器的单位容量是已知的,可求出需投入的并联电容组数。额定电压UN下并联电容器组的单位容量为QN-unit,则电容器实际投入的组数[n]为
[n]=QC/QN-unit
(7)
式中:[n]为并联电容实际投入组数。将电容器组在电压U下的无功功率输出用Q″表示。
(8)
异步发电机并网后节点注入的有功功率P和无功功率Q分别按式(9)、式(10)计算。
P=PG-PL
(9)
Q=Q″-Q′
(10)
式中:PL为节点原有的负荷功率。
在潮流计算中,P-Q(V)节点转换成PQ节点的处理方式在于,先根据异步发电机注入的有功功率P、每次迭代后得到重新修正的电压值U,结合式(2)~式(4)计算出发电机吸收的无功功率,再根据式(5)~式(8)计算出需要补偿的无功功率和需要并入的并联电容器组数。最后根据式(10)计算出注入节点的无功功率[8]。
3 考虑DG模糊接入的静态电压稳定指标模型构建
静态电压稳定性分析是采用潮流方程分析系统在受到扰动时的电压稳定性问题。认为电压稳定则潮流方程存在可行解,反之则无解[9]。在综合比对多种方法之后选择基于潮流解存在的静态电压稳定指标作为本文研究所用的指标。

图3 简单两节点系统
以简单的两节点系统(见图3)对潮流解存在的静态电压稳定性指标进行分析推理。
该简单两节点系统的有功及无功损耗可按式(11)~式(13)进行计算。
(11)
(12)
(13)
式中:Pj和Qj分别为等值到节点j的有功功率和无功功率;Ui和Uj分别为节点i和节点j的电压;Rij和Xij分别为节点i和节点j之间的电阻和电抗。将式(13)展开得:
(14)
令:
(15)
(16)
式(14)变为:
(17)
(18)
(19)
(20)
(21)

(22)
对式(22)化简可得:
(23)
令:
(24)
式中:L为描述节点j的静态电压稳定性指标。根据上述方法求出每个节点的L值,根据L值的大小能够判断电压的稳定水平。节点电压U只有满足L≥0才算稳定,L越小,表示该点的电压稳定水平越低,L最小的点即是电压最可能发生崩溃的点。
4 算例仿真
4.1 P-Q(V)型分布式电源接入对配电网静态电压稳定性的影响
以异步风力发电机接入IEEE 33节点配电系统为算例。在拟定方案前先对异步发电机相关电气参数进行说明,如表1所示。

表1 异步发电机电气参数 Ω
另设定风力发电机的单机容量为600 kW,单台并联电容器的额定容量为40 kvar,额定电压均为0.69 kV。为研究风力发电机组接入大小、位置、是否进行无功补偿,以及功率因数等对配电网静态电压稳定性的影响,拟定四个方案,见表2。
4.2 四种不同方案下仿真结果
图4~图7的仿真结果显示。方案一P-Q(V)型DG并网后进行无功补偿对静态电压稳定指标L的提升量大于不进行无功补偿时的提升量,且补偿后cosφ越小对电压的改善越明显,越有利于系统的稳定。当然无功补偿需要限制在一定的范围内,若过大可能会导致某些节点的电压崩溃。方案二在相同功率因数(cosφ=0.90)下,DG接入容量越大,电网节点电压的提升越大,越有利于系统的稳定运行。

表2 P-Q(V)型DG接入配电系统四种方案

图4 方案一补偿后不同功率因数下DG接入的L指标

图5 方案二不同容量DG接入的L指标
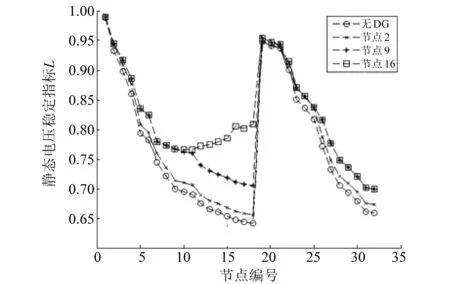
图6 方案三主馈线不同位置DG接入的L指标

图7 方案四同一引出馈线不同位置DG接入的L指标
方案三P-Q(V)型DG接入主馈线后,靠近末端接入对电压的提升量大于靠近电源首端的接入,更有利于系统的电压稳定。方案四P-Q(V)型DG接入同一引出馈线,靠近引出馈线末端对电压的提升量大于靠近引出馈线首端。
5 结束语
本文基于已有对分布式电源接入配电网对静态电压稳定性影响研究的基础上,考虑了DG电源出力和负荷接入模糊性对系统电压稳定性的影响。以异步发电机为例,对异步发电机并网模型简化,构建基于潮流解存在的静态电压稳定性指标L。设置P-Q(V)型DG按不同容量、位置和是否无功补偿等多种方案并网,通过仿真分析验证了这些因素对配电网电压稳定运行有重要影响,并验证了模型求解的有效性,为DG接入配电系统可靠运行提供参考。

