一类对称群的胞腔
罗 新, 王利萍
(北京建筑大学 理学院,北京102616)
1 引 言
1979年,Kazhdan和Lusztig提出了著名的Kazhdan-Lusztig理论.胞腔是该理论中的一个主要研究对象.为了研究Coxeter群的相关代数结构,Kazhdan和Lusztig根据左(右)等价关系,把群元素划分成不同的等价类,即双边胞腔、左(右)胞腔[1].当W是一个Weyl群时,Barbasch, Lusztig, Joseph, Vogan等人对其胞腔进行了研究.Weyl群中胞腔在李型群的表示理论以及半单李代数的普遍包络代数的本原理想理论中都有重要的应用[2].

对于对称群Sn,它有着很好的组合方面的结论和性质,更希望有方便好用的工具可以描述和计算对称群的双边胞腔(或左胞腔、右胞腔),从而应用到表示理论中.文章主要分为三部分,首先介绍了对称群以及胞腔等基本概念,并且指出了Sn内不等价的不可约表示、其每一个左胞腔所对应的W-图与n的整数无序划分之间存在关系;其次,通过计算机编程,实现了用Matlab构建标准Young表,对于对称群中的任意一个置换,可以很快得出其所对应的标准Young表;最后,运用程序给出了一类对称群所对应的双边、右(左)胞腔的个数.
2 预备知识
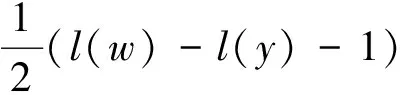
2.1 双边胞腔及左(右)胞腔
定义1[1]对于每一个元素w∈W,令
L(w)∶={s∈S|sw L(wi-1)⊄L(wi) (L(wi-1)⊄L(wi) 或R(wi-1)⊄R(wi)). 类似的,对应于关系w≤Lu,可以定义w≤Ru. 这些关系≤L,≤R,≤LR是W上的预次序. 定义2[1]对于W中的元素w和u,如果满足关系w≤Lu≤Lw(w≤LRu≤LRw),则称它们满足关系w~Lu(w~LRu). 类似的,也可以定义w~Ru. 关系~L,~R,~LR为W中的等价关系,它们对应的等价类分别称为W的左胞腔,右胞腔,双边胞腔. 定义3[1]给定一个Coxeter群W, A=为整系数的Laurent多项式环,q为一个变量,定义在A上的代数H称为一个Hecke代数,H有一组典范基{Cw|w∈W},即为Kazhdan-Lusztig基. 对于任意一个Coxeter群W,Lusztig首次引入a函数:a∶W→∪{∞}. 该函数是研究胞腔以及计算Kazhdan-Lusztig多项式首项系数的一个极其重要的工具. 给定x,y∈W,有 定义5[7]对任意z∈W,定义 定义6[8]整数无序划分是指把整数分解成若干整数的和,若各部分不允许出现0值时,则称各部分为类,即 引理1[9]两个置换g1,g2∈Sn共轭⟺它们对应着n的同一划分. 由引理1知,Sn的共轭类和n的划分之间一一对应,因此,Sn内共轭类的个数等于n的不同划分的个数. 引理2[10]设G是有限群,|G|=g,F是代数封闭域,且charF=0或charF=p但p不整除|G|,又设G的共轭类数为s,则G恰有s个不等价的不可约表示. 对于每一个确定的正整数n,其所对应的对称群Sn显然是一个有限群,因此符合引理2,根据引理1和引理2,可以得到以下结论: 定理1Sn内不等价的不可约表示的个数等于其所对应的共轭类的个数,并且等于n的整数无序划分的个数. 引理3[1]令X是对称群W=Sn的一个左胞腔,Γ是与X相关的W-图,ρ是对应于Γ的代数H的表示,则ρ是不可约的,并且Γ的同构类只取决于不可约表示ρ的同构类,与X无关. 由引理3知,Sn的每一个左胞腔所对应的W-图Γ的同构类与Sn的不可约表示有着紧密的联系. 对于对称群W=Sn,定义单反射集S由以下元组成: si=(i,i+1),i=1,2,…,n-1. 并且规定Sn中置换的乘法是从右向左的.可以根据Robinson-Schensted法则来描述W的胞腔分解情况[11].同时,我们也可以较为容易地计算出相应对称群的a函数. 对于整数n的一个划分λ,都可以找到一个Young表Fλ与之相对应.该Young表由n个盒子组成,每一列的长度由λ的分量所确定,且按照Robinson-Schensted法则,用1,2,…,n来填充盒子.如果用来填充盒子的数字按列从上到下递增且按行从左到右递增,就称该表是一个标准的Young表.该法则定义了一个从Sn到标准Young表对组成的集合上的双射θ∶w→(P(w),Q(w)). 对任意的i=1,2,…,n,令w(i)=ji,标准Young表定义如下: 令T0是一个Young图,接下来利用数学归纳法,按照法则,把数字j1,j2,…,jn-1依次填入到n-1个盒子中,这样便定义好了一个Young表Tn-1. 现在定义Young表Tn:如果jn比Tn-1的第一行中的每一个数字都大,则在Tn-1的第一行的后面再增加一个盒子,并且用jn标记便得到了Tn;否则在Tn-1中找出比jn大的那个最小的数字,并把它记为z,此时用jn来替换z,而对于z,按照上面同样的方法,把它插入到Tn-1表的第二行中,这样经过一系列的比较、替代、换行……,最终得到的Young表就是Tn. 令P(w)=Tn,则它就是一个标准的Young表.相对应地,Q(w)∶=P(w-1). 定理2[12]令y,w是Sn中的元素,则有 (i)y~Lw当且仅当Q(y)=Q(w); (ii)y~Rw当且仅当P(y)=P(w); (iii)y~LRw当且仅当P(y)和P(w)有相同的型. 命题1(i)w,u∈Sn,若a(w)=a(u)且w≤LRu,则有w~LRu[7]; (ii) 在Sn中,a函数的不同函数值的个数小于等于群所对应的双边胞腔的个数.w,u∈Sn,若w~LRu,则必有a(w)=a(u);但反之,若a(w)=a(u),不一定必有w~LRu,即w,u未必在Sn的同一个双边胞腔中; (iii)w,u∈Sn,若w~LRu,则未必有w~Lu或w~Ru成立.反之,若w~Lu或w~Ru成立,则w~LRu. 例如:在A3型Weyl群中,有s2s1s3~LRs1s3s2,但s2s1s3~Ls1s3s2和s2s1s3~Rs1s3s2均不成立. 给出对称群中的一个元素,在画它所对应的Young表时,若所给元素的长度较短,则很容易画出Young表,而一旦所给元素的长度较长,Young表的给出较为困难.因此有必要借助计算机编程,以便更加高效地解决问题.根据标准Young表的相关描述,可以很清楚地看到:对于一个给定的Sn中的置换,构建标准Young表的过程实际是一个具有递归思想的图表构建过程,因此可以应用matlab编程[附录1],从而快速实现标准Young表的构建. 对于任意给出的Sn的置换,可以通过程序来给出它们所对应的标准Young表.下面以n=22,30为例: 12711141516369132148122051710191822图1 置换y对应的Young表 137101322232481115253056169121814172619212024272829图2 置换z所对应的Young表 引理4[8]整数无序划分的相关递推公式 对于任意的正整数n,可以运用C语言软件,根据整数无序划分的要求,得到n的每一种具体的划分[13].根据标准Young表的相关描述,对于n的每一种具体划分,令第一列有n1个盒子,第二列有n2个盒子,……,第k列有nk个盒子,并且每一列第一个盒子左右水平对齐,这样就把n的每一种划分,对应到同一种型的Young表,根据定理2(iii),可以得出以下定理: 定理3Sn的双边胞腔的个数与n的整数无序划分的个数相等. 对于Sn,由于其双边胞腔的个数,等于n的按递减排序的划分个数,而在排列组合中,符合这种条件的划分,就是n的无序k-划分,所以要求Sn的双边胞腔的个数,实际上就是求符合一定条件的n的划分个数.在这里,根据引理4中整数无序划分的相关递推公式,运用matlab[附录2]编程软件,快速求出不同的正整数n所对应的划分个数Pn,即Sn的双边胞腔的个数. 在对称群Sn中,假设P(y)是一个型为λ=(λ1≥λ2≥…≥λk)的Young表,则有 根据a函数的计算公式,可以很快得到:n的每一种具体划分,都会对应一个a函数,同时也对应一种型的Young表,也即符合这种型的标准Young表所对应的Sn中的元素,都在同一个双边胞腔中.这样就把Sn中的元素划分到了不同的双边胞腔中,从而得到了Sn的双边胞腔分解. 在对Sn中的元素进行标准Young表的构建过程中,很容易得到:在同一个双边胞腔中的元素,都会对应相同型的标准Young表,所以也可以间接通过标准Young表的型数,来得到双边胞腔的个数,而标准Young表的型数又是由n的无序划分所决定的;在同一个右胞腔中的元素,都会对应相同的标准Young表.由于当n比较大时,n!是一个比较大的数,所以为了得到Sn所对应的右胞腔分解及其个数,不妨换个角度思考问题:在n的无序k-划分的基础上,给出一种具体划分,便可以得到一种型的Young表,然后用matlab进行编程,把从1到n的这些数填入这种型的Young表中,保证得到的是标准Young表.通过统计满足给定型的标准Young表的个数,便可得到它在这种情况下的右胞腔分解个数,即这种型所对应的双边胞腔中包含的右胞腔的个数.这样把Sn中所有双边胞腔所包含的右胞腔的个数一一都求出来再求和,便可以求出Sn的右胞腔的个数[附录3].由于Q(w)=P(w-1),根据定理2,可得:在对称群中,左胞腔的个数等于右胞腔的个数. 由于计算机内存和算法的限制,在这里给出了当n≤10时,Sn所对应的右胞腔分解个数.当n比较大时,Sn所对应的双边胞腔分解个数,所受影响较小,在这里只列出当n≤20时,Sn的双边胞腔分解个数.下面以S4为例: 例其生成元为s1=(12),s2=(23),s3=(34),并且 4=4=3+1=2+2=2+1+1=1+1+1+1, W={e,s1,s1s2,s1s2s3,s2,s2s1,s2s3,s3,s3s2,s3s2s1,s3s1,s3s1s2,s2s1s3,s2s1s3s2,s1s2s1, s1s2s1s3,s1s2s1s3s2,s2s3s2,s2s3s2s1,s2s3s2s1s2,s3s1s2s1,s3s1s2s1s3,s1s2s3s2,s1s2s3s1s2s1}, 得到这些元素所对应的标准Young表如下: 1234图3 1342图4 1243图5 1234图6 1324图7 1234图8 1423图9 1234图10 1324图11 1234图12 根据定理2,可以得出S4的10个右胞腔为 R1∶{e};R2∶{s1,s1s2,s1s2s3};R3∶{s2,s2s1,s2s3};R4∶{s3,s3s2,s3s2s1};R5∶{s3s1,s3s1s2}; 表1 S4的右胞腔所对应的Young表及a函数值 根据定理2以及整数4的无序划分数目,综合上面图表可知,对称群S4所对应的标准Young表有5种型,因此它有5个双边胞腔,分别为 由于篇幅限制,以下是运行的部分结果 表2 Sn所对应的右胞腔和双边胞腔的个数 本文主要借助计算机编程,得出了以下主要研究结论: (i) 指出了Sn内不等价的不可约表示、其每一个左胞腔所对应的W-图与n的整数无序划分之间存在关系; (ii) 对于对称群中的任意一个置换,实现了用Matlab快捷构建标准Young表; (iii) 以n的整数无序划分的组合公式为出发点,运用编程,分别计算了一类对称群的双边胞腔以及右(左)胞腔的个数; (iv) 从解决问题的角度出发,体现了数学与计算机的紧密结合,这将是一段时间内解决数学问题的有效途径. 致谢本文的完成得到了海军航空大学司守奎教授的帮助,他对本文的部分编程提出了有益的建议.同时,也要感谢审稿人对本文提出的宝贵建议. 附录1(Young表的构建) clc, clear m=input(′请输入正整数m=
′); A=[1∶m;randperm(m)] a=A(2,∶) %生成一个1到n的随机全排列 n=length(a); b=cell(1,ceil(n/2)); %初始化细胞数组 b{1}=a(1); k=1; for i=2∶n if all(a(i)>b{1}) b{1}=[b{1},a(i)]; else ind=find(b{1}>=a(i),1,′first′); %从头开始找第1个数 t1=b{1}(ind); b{1}(ind)=a(i); j=2; while 1 if length(b{j})<1 %b{j}为空 k=k+1; b{k}=t1; break; elseif all(t1>b{j}) b{j}=[b{j},t1]; break; else ind=find(b{j}>=t1,1,′first′); %从头开始找第1个数 t2=b{j}(ind); b{j}(ind)=t1; t1=t2; j=j+1; end end end end b(cellfun(@isempty,b))=[]; %删除细胞数组的空元素 celldisp(b) %显示细胞数组的所有元素值 附录2(计算对称群的双边胞腔个数) clc, clear n=input(′请输入正整数n=
′); a=eye(n); for i=2∶n for j=1∶i-1 if j<=i-j a(i,j)=sum(a(i-j,[1∶j])); elseif j>i-j a(i,j)=sum(a(i-j,[1∶i-j])); end end end a m=sum(a(end,∶)) %计算分解的个数 附录3(计算对称群的右胞腔个数) clc, clear %m=input(′请输入n划分的k元数组∶
′) m=[1 2 3 4]; m=sort(m,′descend′); %按降序排列 n=sum(m); %计算n的取值 L1=length(m); %划分的个数 b=perms([1∶n]); %生成1,2,…,n的全排列 L2=size(b,1); %计算全排列的个数 L=0; %计数初始化 t=cumsum(m);s=[1,t(1∶end-1)+1]; %每一段数据的终点和起点编号 e=cell(1); %初始化细胞数组 for i=1∶L2 a=2*n*ones(L1,m(1)); %矩阵初始化 c=b(i,∶); %利用第i个全排列 for j=1∶L1 a(j,[1∶m(j)])=sort(c(s(j)∶t(j))); %第i个全排列构造的分解 end d=a; d=sort(d); %逐列按照从小到大排列 if isequal(a,d) %相等时满足要求 for k=1∶length(e) if isequal(e{k},d) break; %与已经构造好的数组相等,不保存 end if k==length(e) %与已经构造好的数组不重复 L=L+1; e{L}=d; %保存 end end end end for j=1∶length(e) a=e{j}; a(a==2*n)=0; e{j}=a; %把2n替换为0 E{j}=e{j}′; end celldisp(E) %显示细胞数组的内容
2.2 a函数

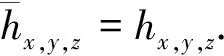

2.3 n的整数无序划分与Sn的关系
3 R-S法则下的Young表构建




4 Sn的双边胞腔及右胞腔
4.1 n的无序划分与Sn的双边胞腔

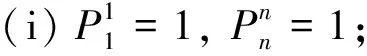
4.2 Sn的右胞腔个数




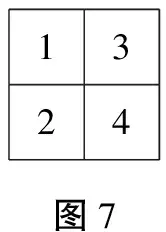





R6∶{s2s1s3,s2s1s3s2};R7∶{s1s2s1,s1s2s1s3,s1s2s1s3s2};R8∶{s2s3s2,s2s3s2s1,s2s3s2s1s2};
R9∶{s3s1s2s1,s3s1s2s1s3,s1s2s3s2};R10∶{s1s2s3s1s2s1}.

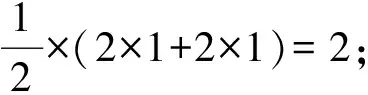
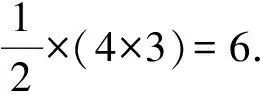


5 结 论

