解线性方程组迭代法的若干几何研究

卢兴江， 金通洸

(浙江大学 数学科学学院，杭州310027)

1 引 言

迭代法是解线性方程组常用的方法，如著名的Jacobi迭代法，Gauss-Seidel迭代法和SOR迭代法[1]等.但对这些迭代过程的认识、收敛性分析等一般是从分析和代数上去研究，例如一个迭代法的收敛与否决定于相应迭代矩阵的谱半径是否小于1，而求谱半径并非易事，而且仅从谱半径去认识迭代法的收敛性是不够的，一个简单的事实是：对某些线性方程组，若变换各个方程的次序，会改变一些迭代法的收敛性，而解的存在与否是和这些方程的次序无关的.要对这样的问题作出解释，揭示出迭代法的几何本质是重要的.下面将从几何上提出两种迭代过程，从而得到解线性方程组迭代法的几何实质.

2 记 号

记n阶线性方程组为

Ax=b,

(1)

其中A=(aij)n×n∈n×n为n阶系数矩阵，b=为n维常数向量，x=(x1,x2,…,xn)T为n维未知向量.

记Ai=(ai1,ai2,…,ain),fi(x)=bi-Aix,i=1,2,…,n，则(1)即为

fi(x)=0,i=1,2,…,n.

这n个方程分别代表n个超平面，记为πi,i=1,2,…,n.即

πi∶fi(x)=bi-Aix=0，

其中(Ai)T为πi的法向量，i=1,2,…,n.

3 迭代法的两个基本几何过程

对线性方程组(1)，首先我们从几何上来看两个基本迭代过程.

(Ⅰ) 反射过程(反射迭代)

对方程组(1) 的n个超平面πi,i=1,2,…,n, 选定一组方向(向量)Ei∈n,i=1,2,…,n, 且E1,E2,…,En线性无关.则反射迭代为这样一个过程(如图1，其中x*为方程组的解)

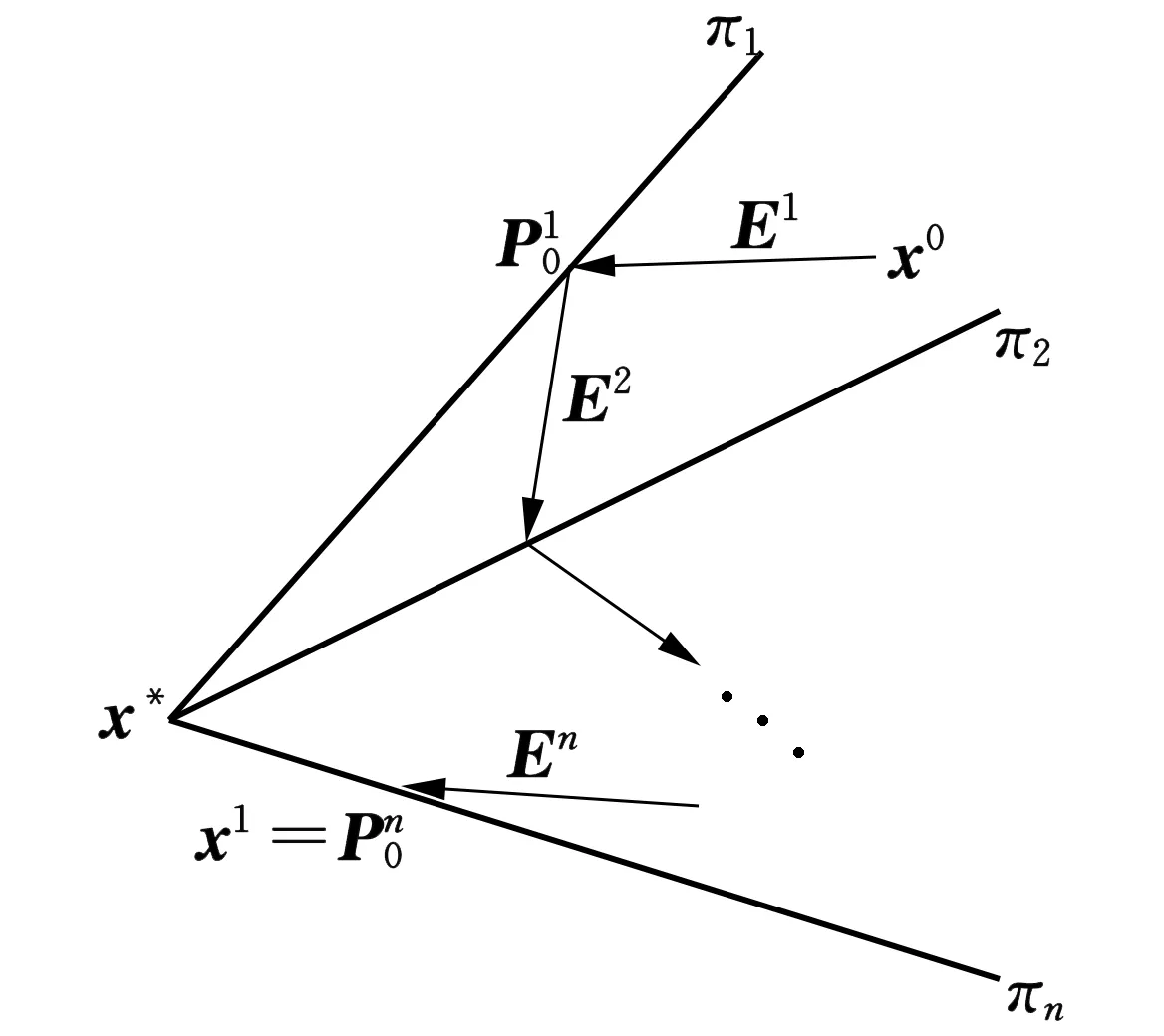
图1 反射迭代

① 选取初值(初始点)x0∈n；

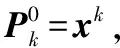
③ 这样得到迭代向量序列{xn}∶x1,x2,…,xn,…

以上过程称为反射过程，或反射迭代.

定理1对方程组(1)及一组线性无关的方向E1,E2,…,En，若A非奇异，且Ai·Ei≠0 (i=1,2,…,n)，则

(i)反射迭代可以一直进行下去；

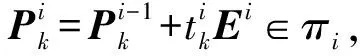
(2)

其中(Rij)n×n称之为关联矩阵，Rij称为关联系数.

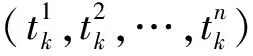
在反射迭代中，取不同的一组方向Ei(i=1,2,…,n)，就可得到不同的迭代法.

定理2对方程组(1)，若取一组线性无关的方向

Ei=εi=(0,0,…,0,1,0,…,0)T(εi第i个分量为1，其余分量为0)i=1,2,…,n,

则反射迭代即为Gauss-Seidel迭代法.

证若在反射迭代中取

Ei=εi=(0,0,…,0,1,0,…,0)T,i=1,2,…,n,

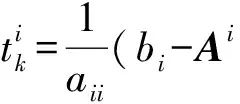
即

这恰为Gauss-Seidel迭代法计算表达式[1].

因此，Gauss-Seidel迭代法是一种反射迭代过程. 从这个几何本质可以看到，Gauss-Seidel迭代法的收敛性是与方程组的各方程(超平面)的次序是有关系的，因为它与“坐标”εi(i=1,2,…,n)有关，如图2和图3相同的两个方程(两张“超平面”)，次序不同，收敛性不同 .

图2 G-S迭代收敛 图3 G-S迭代发散

如果在上述反射过程中引进一个伸缩因子，则有以下迭代过程，我们称之为伸缩反射过程(伸缩反射迭代)：

① 选取初值(初始点)x0∈n；

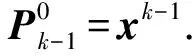
图4 伸缩反射迭代

③ 这样得到迭代向量序列{xn}∶x1,x2,…,xn,….

显然，伸缩反射迭代中若取所有的伸缩因子为1，则伸缩反射过程即为前面的反射过程 .

定理3对方程组(1)和一组线性无关方向Ei，若AiEi≠0(i=1,2,…,n)，则

(i) 伸缩反射迭代可以一直进行下去；

(ii) 对任意给定的初值x0∈n，存在唯一确定的伸缩因子使得迭代n步即得方程组的精确解,即有x1=x*.

对于(i)的证明类似于定理1的(i)的证明 .

对于(ii)，因为

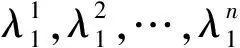
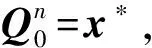
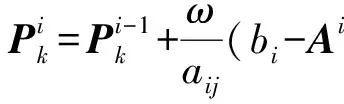
此恰为SOR迭代法计算表达式[1].

所以，SOR方法为伸缩反射过程的一个特例.

定义1在n维空间中，n-1张超平面的交线称为棱，与此n-1张超平面法向皆垂直的方向称为棱方向.

记

其中Δij为A=(aij)n×n中aij的代数余子式.

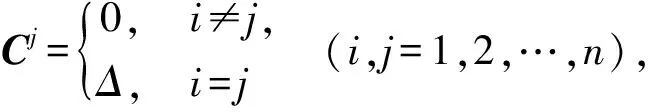
其中Δ=det(A).

因此，对方程组(1)中的n个超平面，Ci(i=1,2,…,n) 即为n个棱方向.

定理5若取Ei=Ci(i=1,2,…,n)，则对任何初值x0，反射过程进行n次即得方程组(1)的精确解，即x1为方程组(1)的解.

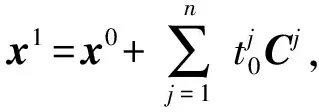
即x1为方程组(1)的解.

由定理5知，选取Ci(i=1,2,…,n)为反射方向，有限步(n步)迭代可得到方程组的精确解.

推论1若取Ei=Ci(i=1,2,…,n)，且取初值x0=0时，则反射迭代所得x1即为方程组(1)的克兰姆[2](Cramer)法则解.

于是

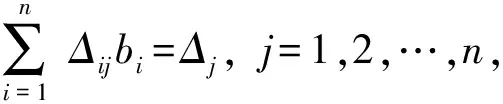
(Ⅱ) 张伞过程(张伞迭代)

选定一组方向(基)Ei(i=1,2,…,n)，对方程组(1)，张伞过程为(图5)：

图5 张伞迭代

① 任取x0∈n；

③ 这样得到迭代向量序列{xn}∶x1,x2,…,xn,….

事实上，这把伞为一个仿射标架：{xk,E1,E2,…,En}，求方程组(1)的解x*就是在此仿射标架中求出x*的“坐标”.

定理6对方程组(1)，若取一组线性无关的方向Ei=εi,i=1,2,…,n, 则张伞过程即为Jacobi迭代法.

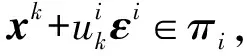
即

此即为Jacobi迭代法计算表达式[1].

从上述可知，Gauss-Seidel迭代法与Jacobi迭代法有着不同的几何本质，前者是反射过程，后者为张伞过程. 在一般情况下反射过程比张伞过程收敛快，所以通常说Gauss-Seidel迭代法比Jacobi迭代法收敛快，但这两个迭代过程本质不同，因此存在对有的方程组Gauss-Seidel迭代法发散而Jacobi迭代法收敛的情况也就不足为奇了.

4 降维迭代法

由上面所述，选取棱方向进行反射迭代可有限步得到精确解，但是计算棱方向的计算量太大，所以在实际计算时不宜采用. 下面将找出一组容易计算的方向Ei(i=1,2,…,n)，并能迭代有限步得到方程组(1)的精确解，将它称之为降维迭代法.

引理1若对方程组(1)，反射迭代的方向E1,E2,…,En满足

AiEj=0，i=1,2,…,n-1;j=i+1,i+2,…,n.

定理7若Ei(i=1,2,…,n) 满足引理1条件，则反射迭代n步即得方程组(1)的精确解，即x1为精确解.

设A1,A2,…,An线性无关，记hij=Ai·Aj(i,j=1,2,…,n).令

(3)

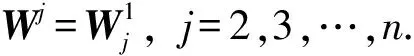
①E1=A1；

②E2=W2；

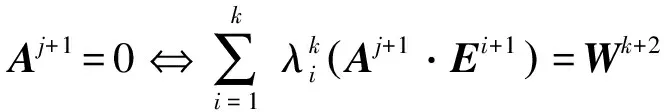
确定，即由

(4)

称这样构造的一组方向Ei(i=1,2,…,n)为降维方向.

由以上易知，如果Ei(i=1,2,…,n) 为降维方向，则有

Ej·Ai=0，i=1,2,…,n-1;j=i+1,i+2,…,n.

定理8设Ei(i=1,2,…,n)为降维方向，则对方程组(1)，反射迭代n步即得精确解.

证由引理1、定理7和降维方向的构造即得.

以降维方向进行反射迭代解线性方程组(1)的方法称其为降维迭代法.用降维法求解时，称反射迭代n步为迭代1次，因有计算误差，如果迭代1次误差不满足要求，可以将得到的x1作为x0继续迭代，这时因Ei(i=1,2,…,n)已经构造好，所以继续迭代时计算非常方便，计算量很小，但效果很好.

数值例子[3]：

精确解为x*=(-1,-1,…,-1)T.

以‖x-x*‖∞<ε来控制精度. 计算结果表明，用降维法迭代4次即得精度为10-6的解.

通过计算量分析，降维法与共轭梯度法为同一数量级，但降维法不要求A为对称正定，只要A非奇即可. 且数值例子表明，降维法比共轭梯度法更有效. 例如：

对Ax=b用降维迭代法迭代2次即得精确解.

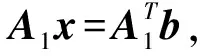
5 总 结

致谢本文是基于博士阶段的工作，感谢导师金通洸先生的悉心指导.也以此文表示对金老师的无限怀念.