挖掘例题的延伸价值 以点带面提升数学素养

福建 卢秀敏 包 喜

“学习数学意味着解题”，解题教学是数学教学的重要组成部分.通过例题教学,巩固知识，辨析概念，通过例题教学，提高分析问题、解决问题的能力，进而提高发现问题、提出问题的能力，通过例题教学，提升数学素养，都是例题教学的重要功能.但在教学实践中，我们发现一些教师的教学存在着就题论题的现象，没有充分挖掘例题的潜在价值，停留在浅层次的水平上，这是亟待改变的.本文就此展开探讨，期望对教师如何挖掘例题的延伸价值，以点带面提升数学素养有所帮助.

1.一题多变，提升数学应用素养

【例1】一个袋子中有5个大小相同的球，其中3个白球，2个黑球，现从袋中任意取出一个球，取出后不放回，然后再从袋中任意取出一个球，则第一次为白球，第二次为黑球的概率为

( )

本题属于古典概型的基本题型，解答过程如下：

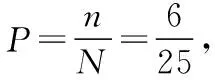
本题通过“举一反三”，将古典概型的几种命题方式逐一解析，通过教师的分析，帮助学生辨别不同的概率模型，横向触类旁通，使学生通过一道题演练这一个点，就能全面复习一个知识面.

2.一题多点，性质成串，提升数学探索素养

( )

知识点一：三角函数中，y=Asinωx,y=Atanωx是奇函数，y=Acosωx是偶函数，故“已知函数f(x)=cos(ωx+φ)(ω>0,0<φ<π)是奇函数”这一条件指向函数的转化，考查了三角函数的基本性质——奇偶性.

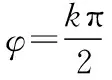
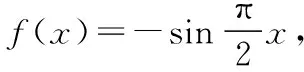
波利亚曾说：“丰富而有条理的知识储备是解题者的至宝”.总结本题的研究过程，发现本题综合考查了三角函数的基本性质：奇偶性、对称性、周期性、最值、单调性及三角运算公式——诱导公式.通过本题的分析及补充延伸，可使学生将基本初等函数的代表之一“三角函数”的七个性质作逐一复习及区分，取得了良好的复习效果.而且本题中各个知识点之间的有效融合，可使学生在解题过程中提升逻辑推理、数据分析、数学建模、直观想象的数学核心素养.

3.一理多用，提升数学文化素养

【例3】如图,有8个村庄分别用A1，A2，…，A8表示.某人从A1出发,按箭头所示方向(不可逆行)可以选择任意一条路径走向其他某个村庄，那么他A1从出发,按图中所示方向到达A8(每个村庄至多经过一次)有________种不同的走法.

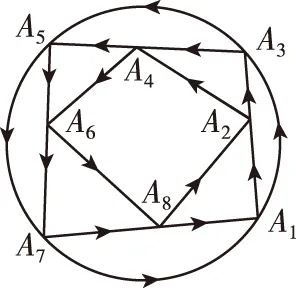
解析：可以从特殊情况出发，寻找变化规律：为方便计数，设从A1到Ai的走法有ai种，则容易看出a2=1，a3=2，a4=3，a5=5,发现a4=a2+a3，a5=a3+a4，所以a6=a4+a5=8，a7=a5+a6=13，a8=a6+a7=21，所以从A1出发，按图中所示方向到达A8(每个村庄至多经过一次)有21种不同的走法.

也可以画出树状图来分析求解.本题实质是斐波那契数列的一部分，是世界名题在初等数学中的应用.所谓斐波那契数列指的是这样一个数列：1，1，2，3，5，8，13，21，34，55，89，…，这个数列从第三项开始，每一项都等于前两项之和.世界名题的特殊化，本来就是高考命题的一个热点，不可忽视.

点评：有时挖掘隐含条件，就等于寻找规律，可锻炼学生敏锐发现数学的能力.中国的数学文化以及世界的数学文化，都是塑造学生数学文化的重要素材，应在欣赏数学之美后，能够应用于生活问题.

【例4】分形几何学是美籍法国数学家伯努瓦B·曼德尔布罗特在20世纪70年代创立的一门新学科，它的创立，为解决传统众多领域的难题提供了全新的思路．如图是按照分层的规律生长成的一个树形图，则第10行的空心圆的个数是________．

解析：由题意及图形知，不妨构造这样一个数列{an}表示空心圆点的个数变化规律，

令a1=1,a2=0,n≥3时，an=an-1+an-2,

本数列中的n对应着图形中的第n行中空心圆点的个数．

由此知a10即所求．

故各行中空心圆点的个数依次为1，0，1，1，2，3，5，8，13，21，34，55，89，…，因此a10=21，

即第10行中空心圆点的个数是21.

点评：本题主要考查了数列的应用，解题的关键是构造这样一个数列{an}表示空心圆点，可以看到第三行起每一行空心圆点的个数都是前两行空心圆点个数的和，由此可以得到一个递推关系，利用此递推关系求解即可．本题实质是当n≥3时，an=an-1+an-2，是斐波那契数列.

再比如，斐波那契数列与台阶问题：小明走台阶，每次可选择走1步或者2步，则只有一个台阶时，只有一种走法，F1=1；两个台阶，走法有2种，一步上一阶或者一步上两个台阶，所以F2=2；三个台阶时，走法有一步一阶，2阶再1阶，1阶再2阶，因此，F3=3；四个台阶时，走法有(1，1，1，1)，(1，1，2)，(1，2，1)，(2，1，1)，(2，2)，共5种方法，故F4=5.以此类推，如果有大于2级的n级台阶，那么假如第一次上一级台阶，剩下还有n-1级台阶，有f(n-1)种上法，假如第一次上2级台阶，剩下n-2级台阶，有f(n-2)种上法，这就表示f(n)=f(n-1)+f(n-2)，因此有数列：1，2，3，5，8，13，21，34，55，89，144，233，….

斐波那契数列与自然、生活、科学上的联系其实还有很多，但是仅仅从这几个例子上我们就可以看出斐波那契数列应用的广泛性，由此我们可以看到数学的美其实是无处不在的,它是一门科学，同时也是一种语言，一种艺术，它如同盛开的茉莉，洁白淡雅，总而言之，数学与自然、生活相伴相随，共同发展.

4.一题多解或多题一解， 提升数学理性思维及数学运算素养

( )

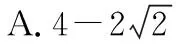
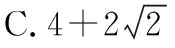
令bn=(an-2)2，则bn+1+bn=4，

GE Ai-qing, ZHANG Dan-feng, CHEN Ji-gang, YU Ming-kun, HU Guo-han, HOU Li-jun, LU Yi-cheng, WANG Jun-yu

bn+2+bn+1=4，于是bn+2=bn，

b1=(a1-2)2,b2020=b2=(a2-2)2，

所以b1+b2020=b1+b2=4，

即(a1-2)2+(a2020-2)2=4.

方法一：

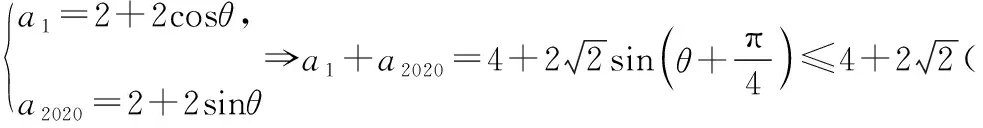
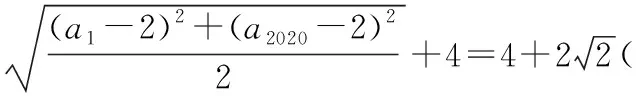
方法三：(a1-2)2+(a2020-2)2=4，

即(a1,a2020)在(x-2)2+(y-2)2=4上，

令z=x+y，即x+y-z=0，

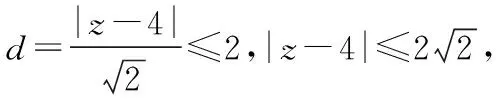
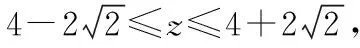
本题是一个数列问题，得到(a1-2)2+(a2020-2)2=4需要配方法，换元法，还需要运用周期性质，是一个比较综合的问题.在得到(a1-2)2+(a2020-2)2=4之后，可用三种思路，一个是三角换元，另一个是均值不等式的变形公式，再一个是应用直线与圆有公共点的性质，每一个思路就是一种方法，都需要数学抽象、逻辑推理、直观想象、数学运算，即理性思维素养.事实上，一题多解，是培养发散思维，沟通知识间互相联系的重要手段，也是以少胜多提升数学素养的有效策略.

( )

C．(1,+∞) D．(0,1)∪(1,+∞)

答案：B.

( )

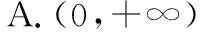
C．(-∞，0) D．(0，1)

答案：B.

( )

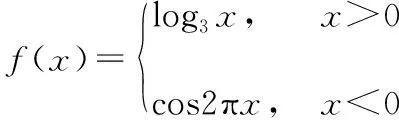
A.7对 B.6对

C.5对 D.4对

答案：B.

( )

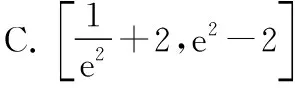
答案：B.

本题有四个问题，以题组的形式出现，其中前三个问题是含参数的分段函数存在关于原点、y轴对称，求参数取值范围的问题.它们有统一的解题策略：如问题(1)(2)首先将y轴一侧的函数图象作关于原点的对称图象，然后考虑此图象与原函数在此侧的函数图象之间的交点问题，问题(3)将y轴一侧的函数图象作关于y轴的对称图象，问题(4)将x轴一侧的函数图象作关于x轴的对称图象，然后考虑此图象与原函数在此侧的函数图象之间的交点问题，通常根据它们的位置关系可建立关于参数的不等式求解．通过如此呈现例题，可以提高学生收敛思维能力，达到由一道题会一类题的目的.