单箱双室变厚翼板CSW简支箱梁剪滞剪切效应
陈玉龙,刘世忠
(兰州交通大学 土木工程学院,甘肃 兰州 730070)
波形钢腹板组合箱梁因其特殊的构造和优于普通混凝土箱梁的力学特性,在当今桥梁工程中应用广泛。其自身结构特点主要体现在波形钢腹板组合箱梁在外力荷载作用下,波形钢腹板承受截面上很大部分的剪力,混凝土顶底板主要承受截面上的弯矩,充分利用了各材料的力学性能。但由于翼板的剪切变形造成的弯曲正应力沿梁宽方向不均匀的“剪力滞”现象[1]存在于各种结构形式的箱梁中,因此同样要对波形钢腹板组合箱梁进行剪力滞效应的研究分析,以便更好地为设计和实际应用提供可靠的理论依据。关于波形钢腹板剪力滞现象的研究,国内学者采用不同的方法进行了大量的研究工作。MA等[2]采用新的空间网格模型来研究波形钢腹板组合梁剪力滞效应,建立了对应的斜拉桥实体模型验证了该方法的有效性和准确性,SHAO等[3]通过模型试验和截面实测应力数据对剪力滞现象进行了分析,周勇超等[4]利用最小势能原理分别研究了等截面和变截面波形钢腹板组合梁的剪力滞效应,周茂定等[5]采用三杆比拟杆法对波形钢腹板简支箱梁的剪力滞系数进行了分析,姜瑞娟等[6]采用能量变分法分别研究了几何参数对波形钢腹板简支和连续箱梁剪力滞效应的影响。上述方法都是在计算中以等厚度的翼板为前提条件进行剪力滞分析,对翼板变厚度波形钢腹板箱梁的剪力滞效应分析鲜有报道。同时在进行箱梁剪力滞分析时,选用的剪滞翘曲位移函数也有很大差异,XU[7]将剪滞翘曲位移函数按照三次抛物线方程进行剪力滞系数计算,CHENG等[8]将剪滞翘曲位移模式设为余弦函数进行剪力滞效应下的挠度计算,肖军等[9]按照四次抛物线方程利用变分法求解了剪力滞控制微分方程及其解析解,以上方法对于剪力滞效应的解析解计算精度有不同程度的影响,因此,选用适当的剪滞翘曲位移函数也是研究分析的一个重要环节。张元海等[10]在分析翼板面内的剪切变形时,验证了剪滞翘曲纵向位移函数以二次抛物线形式分布的正确性,因此,本文在进行剪力滞效应分析时选用这一函数形式。同时,倪元增等[11]认为如果想要得到更加精确的理论值,剪滞翘曲纵向位移函数应当满足全截面轴力自相平衡这一附加条件,该条件在文献[10]中已被证实是可有效提高计算精度的。为了能够更加准确地研究翼板变厚度的单箱双室波形钢腹板箱梁的剪力滞效应,本文在上述文献的基础上,以翼板变厚度的单箱双室波形钢腹板箱梁为研究对象,结合波形钢腹板箱梁受力特点,采用变分法的最小势能原理,建立了翼板变厚度单箱双室波形钢腹板箱梁在考虑剪滞效应和剪切变形双重影响的基本微分方程并进行推导求解,得到翼板变厚度单箱双室波形钢腹板箱梁剪力滞效应的分析方法,并利用有限元分析值对解析值进行验证。
1 翼板变厚度单箱双室波形钢腹板剪滞基本微分方程的建立及求解
1.1 基本假定
1)忽略波形钢腹板对抗弯承载力的贡献;
2)在竖向荷载作用下,截面处混凝土上、下翼板满足平截面假定;
3)波形钢腹板与混凝土上、下翼板之间连接良好且共同工作,不发生相对滑移;
4)不考虑钢筋对截面刚度的影响。
1.2 基本原理
如图1所示的翼板变厚度单箱双室波形钢腹板箱梁,在任意竖向外力荷载q(z)作用下,截面发生挠曲变形,为更好地描述箱梁截面上任一点的纵向位移,选用满足轴向剪滞翘曲应力自平衡的二次抛物线为翼板纵向位移差函数,同时给出组合箱梁竖向挠度w(z)和考虑了剪切变形的纵向位移u(x,y,z)2个广义位移的表达式为:

图1 外力荷载及波形钢腹板箱梁横断面简图Fig.1 Diagram of external load and cross section of corrugated steel web box girder

Ge可通过式(3)进行计算[12]:

式中:G为钢材的理论剪切模量,a,b,c分别为计算需用到的波形钢腹板几何尺寸值,h为波高值,如图2所示。
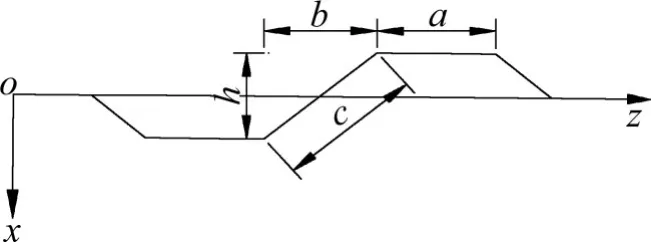
图2 波形钢腹板几何尺寸图Fig.2 Geometrical size drawing of corrugated steel web
本文在对翼板变厚度单箱双室波形钢腹板进行计算分析时,选用的翼板剪滞翘曲纵向位移差函数如下[13]:

d为使箱梁横截面满足轴向剪滞翘曲应力平衡条件而考虑的常数位移值,因本文计算分析中上、下翼板为变厚度形式,其计算表达式较为繁琐,详见式(19),b1,b2,b3,h1,h2表示见图1。对于翼板剪滞翘曲纵向位移差函数,参照文献[10]有如下公式:

根据式(2)可知,截面上任一点的纵向正应变和面内剪切变形为:
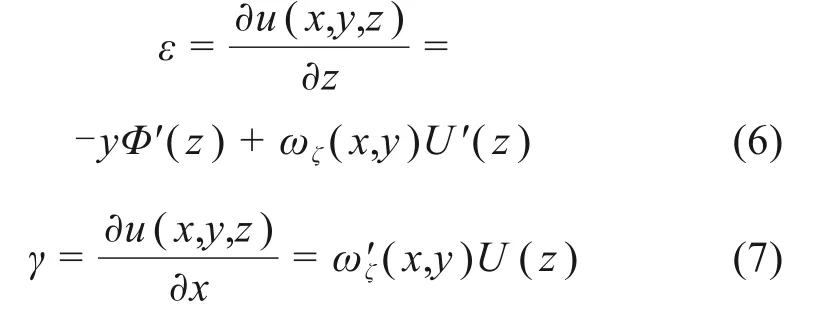
由式(6)~(7)可得,翼板变厚度单箱双室波形钢腹板的顶底板应变能及钢腹板应变能如下:

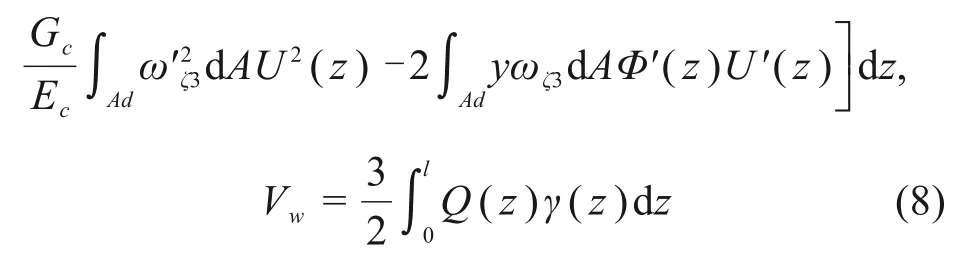
组合箱梁受到外力作用后的外力势能为:

则截面箱梁体系的总势能为:

式(10)中:

Gc及Ec分别为混凝土的剪切模量和弹性模量,Au1,Au2,Ad分别为翼板变厚度箱梁的内顶板,悬臂板及底板横截面面积。


由式(11)微分方程组可得翼板变厚度单箱双室波形钢腹板箱梁的剪滞微分方程为:
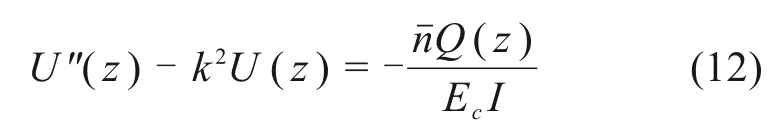
解微分方程可得:

式中:C1与C2为与边界条件有关的常系数;D为与Q(z)有关的特解。
于是根据胡克定律,可得横截面上任一点的纵向正应力和剪力滞系数为:

通过上述计算,可以看出,翼板变厚度单箱双室波形钢腹板的剪力滞控制微分方程与文献[13]中的等厚度单箱双室波形钢腹板的剪力滞控制微分方程形式具有相似性,但Iωζ,Iyωζ及Iω′由于翼板厚度发生变化,等厚度条件下的计算方法不再适用,因此需要重新推导求解。
2 均布荷载及集中荷载作用下的单箱双室翼板变厚度波形钢腹板简支箱梁的剪滞效应分析
2.1 单箱双室翼板变厚度波形钢腹板简支箱梁在集中荷载作用下的剪滞分析
如图3所示,一跨长为l的波形钢腹板简支箱梁在集中荷载作用下,
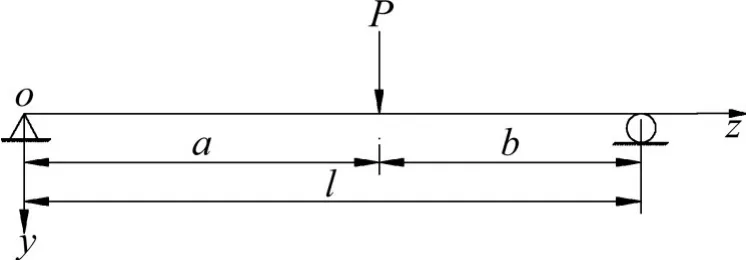
图3 波形钢腹板简支箱梁受集中荷载作用Fig.3 Simply supported box girder with corrugated steel webs subjected to concentrated load
当0≤z≤a时,令ξ=,M1(z)=ξPz,Q1(z)=ξP;
当a 将以上表达式代入式(12)可得: 根据以上4个边界条件及其构成的4个方程式,可得: 所以当0≤z≤a时,将u1代入式(14)有: 当a 如图4所示,一跨长为l的波形钢腹板简支箱梁在集中荷载作用下,根据力学关系可得:,将其代入式(12)可得: 图4 波形钢腹板简支箱梁受均布荷载作用Fig.4 Simply supported box girder with corrugated steel webs under uniform load 将C1,C2及u代入式(14)可得: 鉴于已有文献[4−6,13]等在进行波形钢腹板组合箱梁剪力滞后效应分析时,都按照等厚度翼板条件下的箱梁分析,这与工程实际中的箱梁翼板形式存在较大差异,因此本文将以变厚度翼板为研究对象进行分析。由前述单箱双室翼板变厚度波形钢腹板剪滞微分方程可知,式中的Iωζ,Iyωζ及Iω′计算方法不同于翼板等厚度情况,本文按照翼板面积等效原则,以翼板厚度沿箱梁横截面方向线性变化作为新的条件,仍以原有翼板面积不变为原则进行分析,因此在进行等效计算时,截面的抗弯刚度不发生变化。 如图5所示的箱梁横截面,y1和y2分别为顶板下缘的表达式,y3和y4分别为底板的上缘表达式,y5则为悬臂板的下缘表达式,上述表达式的方程为: 图5 箱梁横断面Fig.5 Cross section of box girder 根据变厚度翼板的各上、下缘方程表达式,将式(4)代入式(5),即可解得常数位移值d为: 式(19)中的y′11和y′12分别为图6(b)中的顶板处A11,A21和A12,A22的各截面形心到中性轴的距离,y′21和y′22则为底板处简化后的相应截面形心到中性轴的距离,A则为图5整个横截面面积。 图6 箱梁左顶板Fig.6 Box beam left roof 如图6所示,对变厚度翼板进行等效计算时,可将实际结构中的翼板面积从图6(a)向图6(b)进行简化,由于翼板厚度相较于箱梁梁高很小,因此为方便计算,简化前后整个截面的中性轴位置保持不变,对于悬臂板和底板的计算也采用同样的等效方法,不再赘述。 以图6为例,利用箱梁左顶板尺寸及式(10)中Iωζ,Iyωζ及Iω′的计算公式对翼板变厚度箱梁不同含义的参数惯性矩进行推导求解: 式(20)~(22)即为图6中顶板A11和A12面积下的截面惯性矩计算公式,对于顶板另一半面积A21和A22,通过计算也可得到相似公式,只是公式中的φ1需改写为φ2,其余系数均不变,由式(18)得:φ1=φ2,因此可得翼板变厚度箱梁左顶板有Iωζ=Iωζ1+Iωζ2=2Iωζ1,Iyωζ=Iyωζ1+Iyωζ2=2Iyωζ1,Iω′=Iω′1+Iω′2=2Iω′1。 由于实际应用中,箱梁横截面大多具有对称性,对于顶板处右边的Iωζ,Iyωζ及Iω′则可利用横截面的对称性进行求解,同样对于底板及悬臂板的各惯性矩数值,利用图6中的简化方式及式(20)~(22)以及箱梁横截面的对称性均可求得,限于篇幅,不再介绍。 本文算例的几何尺寸参考文献[14]算例中的几何跨度和横截面尺寸,将文献[14]算例中的横截面尺寸简化为与图6相似的形式,再按照本文介绍的计算方法进行理论分析。已知混凝土弹性模量为34.5 GPa,泊松比为0.167,波形钢腹板弹性模量为206 GPa,泊松比为0.283,在简支箱梁跨中部位按照文献[14]中的布载方式布置q=30 kN/m的均布荷载,图7为按照文献[14]算例中的实际截面建立的有限元模型图,图8为按照本文要求简化后的截面尺寸,并在截面相应位置设置计算点,最后将计算结果及有限元分析值一并列于表1中。 图7 有限元模型Fig.7 Finite element model 图8 箱梁横截面简化图Fig.8 Simplified cross section of box girder 通过表1中的结果对比可以看出,以本文方法计算得到的结果与有限元软件分析所得结果除在顶板下缘个别计算点处误差达到10%左右外,其余各计算点的结果误差相对较小,最小误差可以达到0.92%,说明本文方法可以满足工程实际的需要。 表1 均布荷载作用下跨中截面应力分析值Table 1 Stress analysis value of mid-span section under uniformly distributed load 对单箱双室翼板变厚度波形钢腹板简支箱梁在集中荷载作用下进行计算分析时,同样按照文献[14]算例中的荷载布置方式布置P=90 kN的集中荷载,由于在集中荷载作用点存在局部荷载效应,因此在表2中不列出该处计算点的应力值。 表2 集中荷载作用下跨中截面应力分析值Table 2 Stress analysis value of mid-span section under concentrated load 由表2结果可以看出,在顶板部位各计算点的计算值与有限元分析值存在较大误差,而在底板处误差相对更小,最小误差仅为0.87%,可见在集中荷载作用下进行分析时,由于集中荷载局部效应的影响,底板处的应力对比情况要好于顶板处。 若按照文献[14]中将箱梁横截面简化为翼板等厚度截面进行剪力滞效应分析时,只需将式(19)~(22)中的φ1,φ2,φ3,φ4,φ5代为0进行计算,计算结果分别列于表3和表4中,并与有限元分析值进行比较。 根据表3的数据分析结果可知,在均布荷载作用下,按照翼板厚度不变计算时,6号与8号计算点理论值与有限元值最大误差分别为44.3%和42.4%,这是由于在利用有限元分析时,应力误差要比位移误差大一个量纲,所以出现较大的变化;同时在等厚度条件下,除顶板少数计算点分析误差比表1变厚度条件下的分析误差有减少外,其余各计算点分析误差与变厚度分析误差相比都有所增大,可见本文采用的变厚度计算方法要优于等厚度计算分析。 表3 均布荷载作用下的跨中截面应力分析值Table 3 Stress analysis value of mid-span section under uniformly distributed load 由图9可以看出,在均布荷载作用下,对于顶底板各计算点而言,本文方法的计算结果与有限元分析结果吻合情况要优于等厚度条件下的计算结果,说明本文方法具有更好的实用性。 由表4的计算结果可以看出,在顶板上缘和个别翼板厚度最小处,变厚度翼板剪滞效应相比等厚度翼板剪滞效应有所增加;而在截面其余计算点处,变厚度翼板剪滞效应都要比等厚度翼板剪滞效应有所减小。从图9中可以看出,变厚度翼板剪滞效应与有限元分析结果下的剪滞效应吻合情况要好于等厚度翼板与有限元分析的吻合情况,可见利用变厚度计算方法,能够更加精确地对波形钢腹板组合梁剪滞效应情况进行分析。 表4 均布荷载作用下的跨中截面剪滞效应对比Table 4 Comparison of shear lag effect of mid-span section under uniformly distributed load 图9 均布荷载作用下的应力对比Fig.9 Stress contrast under uniformly distributed load 由表5的数据分析结果可以看出,在集中荷载作用下,按照翼板厚度不变计算时,9号计算点理论值与有限元值最大误差为35.71%,比变厚度条件下的分析误差增大了12%;除4号计算点分析误差比表2中变厚度条件下的分析误差减少2.12%外,其余各计算点分析误差与变厚度分析误差相比都有所增大,可见变厚度分析方法的实效性更好。 表5 集中荷载作用下的跨中截面应力分析值Table 5 Stress analysis value of mid-span section under concentrated load 由图10可以看出,在集中荷载作用下,对于顶底板各计算点而言,按照本文方法计算的结果与有限元分析结果吻合情况也要好于按照等厚度方法计算的结果与有限元分析结果的吻合情况,说明本文方法更贴合工程实际情况。 图10 集中荷载作用下的应力对比Fig.10 Stress contrast under concentrated load 由表6的分析结果可知,除顶板上缘处变厚度翼板剪滞效应比等厚度翼板剪滞效应有所增大外,在其余各计算点处,变厚度翼板剪滞效应都要比等厚度翼板剪滞效应有所减小;且从图10中可以看出,变厚度翼板剪滞效应与有限元分析结果下的剪滞效应吻合情况也要优于等厚度翼板与有限元分析的吻合情况,可见变厚度翼板剪滞效应要比等厚度翼板剪滞效应更接近工程实际中的剪滞效应现象。 表6 集中荷载作用下的跨中截面剪滞效应对比Table 6 Comparison of shear lag effect of mid-span section under concentrated load 1)在进行箱梁剪滞效应分析时,选取满足轴向剪滞翘曲应力自平衡的二次抛物线为翼板纵向位移差函数,并利用翼板面积等效原则对变厚翼板单箱双室波形钢腹板简支箱梁进行剪滞效应分析所得的解析解与有限元分析值吻合良好,验证了本文方法的正确性。 2)对变厚翼板单箱双室波形钢腹板简支箱梁进行剪滞效应分析时,均布荷载作用下的应力误差要明显小于集中荷载作用下的应力误差,是由于集中荷载作用位置附近的应力扩散效应所致。 3)采用翼板变厚度和等厚度计算方法分别对单箱双室波形钢腹板简支箱梁进行剪滞效应分析时,前者计算得到的应力误差比后者计算得到的应力误差最大可减少33%,可见将复杂形状变厚翼板等效为线形变厚翼板进行剪力滞剪切双重效应分析,不仅极大简化计算,而且提高了计算精度。 4)在均布荷载和集中荷载分别作用下,变厚度翼板剪滞效应总体来说要比等厚度翼板剪滞效应有所减小,并且变厚度翼板剪滞效应更接近实际工程中的剪滞效应现象,因此在工程结构分析中,可以通过变厚度翼板剪滞效应计算方法来对工程实际中的组合梁剪滞效应现象进行分析。



2.2 单箱双室翼板变厚度波形钢腹板简支箱梁在均布荷载作用下的剪滞分析



3 翼板变厚度单箱双室波形钢腹板箱梁截面惯性矩常数计算





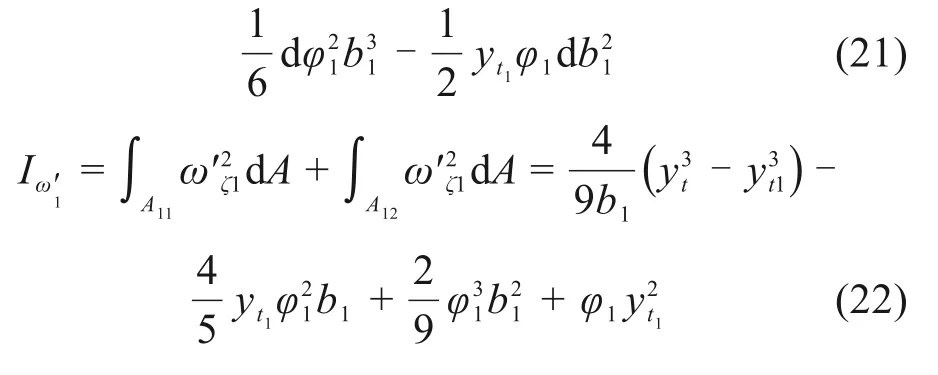
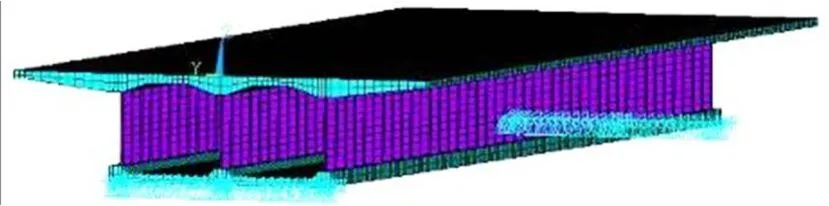
4 翼板变厚度单箱双室波形钢腹板箱梁剪滞效应算例
4.1 均布荷载作用下的剪滞效应分析


4.2 集中荷载作用下的剪滞效应分析

4.3 翼板变厚度与翼板等厚度在均布荷载作用下的剪滞效应对比分析



4.4 翼板变厚度与翼板等厚度在集中荷载作用下的剪滞效应对比分析



5 结论

