完全图线性链的电阻距离

李云翔，徐思奥，潘向峰

(安徽大学 数学科学学院，合肥 230601 )

1 引 言

设G=(V(E),V(G))是顶点集V(G)={v1,v2,…,vn}和边集E(G)={e1,e2,…,em}的简单连通图。在图G中，传统的顶点vi和vj之间的距离记为dij，指连接它们的最短路径的长度。距离是图论中的一个重要不变量，由它导出了许多基于距离的不变量。其中较为著名是Wiener指数[1]，记为W(G)，它是指G中所有顶点对之间距离的和，即

类比于Wiener指数，图G的基尔霍夫指数Kf(G)定义为图G中所有顶点对之间的电阻距离之和[2]，即

(1)

随着基尔霍夫指数研究的不断深入，当把两端点度的大小加入考虑因素之中时，随即产生了度积基尔霍夫指数和度和基尔霍夫指数.Chen和Zhang在 2007 年提出了度积基尔霍夫指数[6]，定义为

(2)

Gutman等人在2012年提出了度和基尔霍夫指数[7]，定义为

(3)

目前，有关电阻距离计算方法有很多，如串并联原理，星-三角变换[8]、消去原理[2]、星网变换[9]、概率公式[10]、组合公式等[11]、代数公式[12-13]。基于上述方法许多特殊图的电阻距离被计算出来，如线性2-树[14]、盆栽网络[15]、硅酸盐网络[16]等。

图的基尔霍夫指数与图的拉普拉斯特征值具有紧密的联系，其数值可以通过图的拉普拉斯特征值求得[17]，对于大部分难以给出拉普拉斯特征值的图，其基尔霍夫指数的求解还较为困难。由于树的基尔霍夫指数与维纳指数是相同的，因此研究带有圈结构的基尔霍夫指数便显得有价值，如杨玉军等人研究了单圈图的基尔霍夫指数。[18]许多结构更为复杂的图也被研究，如给定直径的二部图[19]、广义电晕图[20]、线性交叉四角链[21]等。

线性链系统是由一些具相同结构的平面图组合而成的线性状图类，是一类很重要的图，它和一些化学分子结构有着紧密的联系，如苯类烃，直线状多环芳烃等。而基尔霍夫指数在确定分子不变量中又扮演着重要的角色，因此确定线性链的基尔霍夫指数就显得尤为重要，近些年有关线性链的基尔霍夫指数的文献有很多，如梯形图[22]、梯形状链图[23]、线性六角形链图[24]、线性交叉六角形链图[25]、线性八角形链图[26]、线性交叉八角形链图[27]等。在线性链系统中有两类图，其具有非常鲜明的特点，因而被广泛研究。一类是由圈所构造出的，如梯形图、线性六角形链图等，另一类结构更为复杂的图，是由完全图所构造出的，如直线性2-树[28](见图1(a))、线性交叉四角链[21](见图 1(b))。本文主要研究第二个图类，我们称这样的图类为完全图线性链，记为表示为由m个n阶完全图所组合而成的，其中当n≥4时，相邻的两个完全图共用一条边，不相邻的完全图没有公共顶点和边。图2(a)给出了的图示，由于n阶的完全图不容易通过图示表示出来，所以我们只画出来其部分顶点，以及这部分顶点之间的边，其余顶点和边省略。图2(b)给出了的图示。

图 1 (a)直线性2-树，(b)线性交叉四角链

图

当n=3时，完全图线性链又称直线性2-树，当n=4时，完全图线性链又称线性交叉四角链.文献[27]中研究了直线性2-树的电阻距离及相关结论，文献[21]则研究了线性交叉四角链的基尔霍夫指数。基于此，本文主要通过电网络中的星网变换和消去原理来研究完全图线性链的电阻距离以及的基尔霍夫指数、度积基尔霍夫指数、度和基尔霍夫指数。

2 准备知识

在本节中，给出一些必要的定义和定理。

对于图G=(V(G),E(G))，如果顶点v和u是相邻的，或者说u是v的邻居，用v～u来表示，并且用e=vu来表示这两点之间的边。图G中顶点v的度，记作d(v)，表示v在G中邻居的个数。而与v邻接的所有顶点构成的集合称为v的邻接集，记作N(v)。图G的子图是一个图H，它满足V(H)⊆V(G)，E(H)⊆E(G)且H中边的端点的分配和G中一样，用H⊆G来表示。

如果N表示一个电网络，可以把N看作一个加权图G，其中边的权值是由这条边的电阻表示。为书写方便，接下来不区分图G和相应的电网N。用符号Ω(u,v)来表示顶点u和v之间的有效电阻.当u和v相邻时，用r(u,v)来表示边e=uv上的电阻值。当电网络N中所有边的电阻为1欧姆时，有R(u,v)=Ω(u,v)。在电网络中，串并联原理表述如下。

串联原理若顶点u和v之间仅有n个电阻值分别是r1,r2,…,rn欧姆的电阻串联在一起，则

Ω(u,v)=r1+r2+…+rn

(4)

并联原理若顶点u和v之间仅有n个电阻值分别是r1,r2,…,rn欧姆的电阻并联在一起，则

(5)

在现实中，电阻器的电阻都是正的，然而，引入零和负电阻的概念是必要的。因此对等式(4)和(5)进行扩展，使它们可以包括零电阻和负电阻。[28]

如果一个零电阻与其它电阻串联，则从式(4)来看，它不会影响串联电阻的有效电阻。如果一个零电阻与一些电阻并联，那么根据式(5)，并联电阻的有效电阻为0欧姆。如果一个r欧姆的电阻与一个-r欧姆的电阻并联，那么它们的有效电阻为+∞。这意味着两个电阻连接的顶点实际上是断开的。

从现在起，允许电阻可以为任何实数值。为了便于证明本文的主要结果，首先讨论电路中的两个重要原理。回顾一下图论中一些概念，连通图G的割点是指当把顶点v删除后，使得图G不连通的顶点v。图G的一个块B是G的没有割点的极大连通子图，如果G本身是连通的并且没有割点，则G是一个块。

消去原理[2]设N是一个电网络且其底图G是连通的。设B是G的一个仅包含G的一个割点w的块，如果N′是N通过删除B中除顶点w以外的所有顶点而得到的电网络其底图为G′，则对于任意的u,v∈V(G′)，都有ΩN(u,v)=ΩN′(u,v)。

应用消去原理可以使电阻距离的求解变的简单。如图3(a)所示，电网络N中所有的边的电阻为1欧姆，顶点v,w,z所导出的子图是一个N的块，且v是N的唯一割点，如果从N中移除顶点w,z，得到如3(b)所示的网络N′，则RN(u,v)=RN′(u,v)。在电网络N′中，由串并联原理，易得RN′(u,v)=1，则RN(u,v)=1。

图3 (a)N，(b)N′

接下来引入S-等价网络的概念。

定义1设N、M为两个不同的电网络，令S⊆V(N)∩V(M)，称N和M是S-等价，如果对于任意u,v∈S，都有ΩN(u,v)=ΩM(u,v)。

图4(a)中的电网络称为Δ-电网络，图4(b)中电网络称为Y-电网络.根据图4(b)所示的公式，可以将Δ-电网络转换为等效的Y-电网络，即Δ-电网络和Y-电网络是{u,v,w}-等价的，这些公式最初是由Kennelly[8]于1899年推导出来的，我们称之为三角-星变换。

图 4(a)Δ-电网络，(b)Y-电网络

在实际情况中，对于电网络N，经常面临对其一部分进行操作，从而想要保持其整体性不变，就有了在电路中应用更为广泛的替代原理。

替代原理如果H是N的一个子电网络，H与H*是V(H)-等价的，那么在N中用H*代替H得到的网络N*，对于任意的u,v∈V(N)，满足ΩN*(u,v)=ΩN(u,v)，即N与N*是V(N)-等价的。

称一个图为完全图，表示其任意两个顶点都是邻接的，并将含有n个顶点的完全图记为Kn。设V(Kn)={v1,v2,…,vn}，如图 5(a)。文献[29]给出了Kn中任意两顶点之间的电阻距离，即对于任意的i,j∈{1,2,…,n}且i≠j，都有

图5 (a)Kn，(b)Sn

星图是一个树，指存在一个顶点与其它顶点都邻接，剩下的顶点度为1的图，n+1阶的星图记为Sn。把与其它顶点都邻接的顶点称为Sn的根，记为t，令V(Sn)={v1,v2,…,vn,t}，如图 5(b)，当分配给每条边电阻为欧姆，由消去原理可得，对于任意的i,j∈{1,2,…,n}且i≠j，都有可以发现电网络Kn与电网络Sn是V(Kn)-等价的.结合替代原理，可以容易得到星网变换。

星网变换[9]在任意电网络N中，Kn是其一个子电网络，且每条边的电阻为1欧姆，则Kn可以替换为Sn而不影响电网络中余下的部分电网络，其中Sn中每条边的电阻为欧姆，即新的电网络N*是N的一个等价电网络。

3 主要结果

本节主要通过电路中的消去原理、星网变换、替代原理，研究完全图线性链的电阻距离，同时给出的基尔霍夫指数、度积基尔霍夫指数、度和基尔霍夫指数。

令

其中和

接下来给出完全图线性链中任意点对的电阻距离。

定理1 设为完全图线性链，其中n>4,m≥1，顶点集的划分为则

图

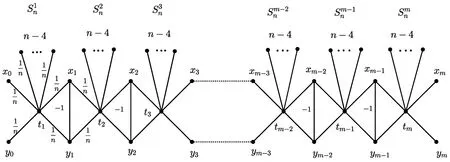
图

对于情形1，当u=xi,v=yi，1≤i≤m-1时，ti和ti+1都是的割点，根据消去原理，只需考虑由{xi,yi,ti,ti+1}为顶点集所生成的子网络Qi，见图8(a)，再由串联、并联原理，容易得所以

对于情形2，当u,v∈V(Ki),1≤i≤m时，ti是的割点，根据消去原理，只需考虑由{u,v,ti}为顶点集所生成的子网络Zi，见图8(b)，通过串联原理，易得所以

图8 (a)Qi，(b)Zi，(c)Wij

对于情形3，当u∈{xi,yi},v∈{xj,yj}，1≤i

对于情形4-6 的证明，与情形3的证明类似，在此省略，不再赘述。

推论1 设为完全图线性链，其中m≥1，顶点集的划分为则

定理2 设为完全图线性链，其中m≥1，顶点集的划分为则

证明由推论 1 以及等式 (1)，可以得

定理3 设为完全图线性链，其中m≥1，顶点集的划分为则

证明结合推论 1 和等式 (2)，可以得

定理4 设为完全图线性链，其中m≥1，顶点集的划分为则

证明结合推论 1 和等式 (3)，可以得

4 结 论

本文主要研究了完全图线性链的电阻距离及基尔霍夫指数。通过引入负电阻，结合替代原理和星网变换，构造出一个与完全图线性链等价的结构简单的电网络，再利用消去原理、串并联原理、星—三角变换，得到完全图线性链中任意顶点对之间的电阻距离。其次给出了的基尔霍夫指数、度积基尔霍夫指数、度和基尔霍夫指数。