锗烯基电极材料的第一性原理研究

李占超 李卓 王思奇 司雪 杨光敏＊

（长春师范大学物理学院，吉林长春 130032）

1 研究背景

自2004 年Geim、Novoselov 等人成功的在实验中分离出石墨烯以来，科研工作者们的目光就迅速向它靠拢，在不断的研究中，人们发现了半导体材料的新大陆，石墨烯所展现出的出色的物理化学特性使得二维材料成为研究热点。相比硅烯而言，锗烯的自旋轨道耦合强度能达到硅烯的10 倍，所以锗烯所产生的量子自旋霍尔效应也比硅烯更强。锗烯还具备一些优良的性质使得它能与半导体工艺更好衔接，因此锗烯在半导体高速纳米电子器件方面有着更为广阔的应用潜力和空间。

2 研究对象

锗烯(Germanene)是一种结构为六角蜂窝状的晶体材料，呈现出褶皱结构，具有一定的曲翘，如图1 所展现的形状。锗烯正格子基矢的晶格常数（图中a1、a2）为4.02Å，两个相邻的锗原子A、B 之间的距离为0.68Å。将两个锗原子所形成的键与Z 轴所成的夹角记为θ（图1（b）），θ 的大小大约为106.5°，这说明了锗烯并非像石墨烯一样是完全平面的二维材料。同时，由于这个夹角比较大，所以锗烯中两个相邻的锗原子之间会存在较大的间隔，这使得锗烯的杂化方式也与石墨烯的杂化方式不同，锗烯不仅更容易形成sp2、sp3的杂化，而且还能使π 键和σ键重合的更加明显，使整体结构相较于石墨烯稳定性更强。

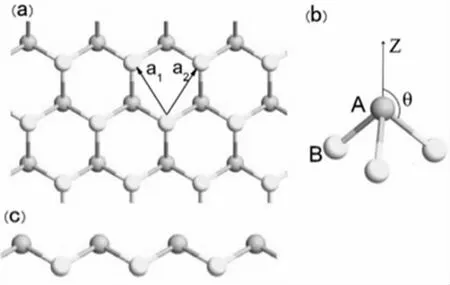
图1 Germanene 的晶体结构

自从发现了石墨烯的存在，科研工作者们的目光就迅速向它靠拢，在不断的研究中，人们发现了半导体材料的新大陆，石墨烯所展现出的优良特性使得二维材料的研究成为了热点。

但是由于能带的间隙性使得石墨烯难以被广泛的应用。这也使得科研工作者们将研究的重心转移到了发现一种与石墨烯一样具有优异的物理性质，同时不存在能带间隙性的新型二维材料。所以后续的研究中，如何弥补石墨烯的缺陷就成为了类石墨烯的研究方向。从图2 中我们可以看出，锗烯的晶体结构虽然看起来与石墨烯极其相似，但是锗烯并非是完全的二维平面，它的结构具有一定的曲翘，锗原子之间出现的是明显的sp3杂化，而非是石墨烯中出现的sp 和sp2杂化。由于锗烯存在曲翘结构，这使得锗烯与石墨烯之间的性能有着不小的差异。锗烯存在狄拉克锥和自旋轨道耦合，导致其带隙会打开。因此相比石墨烯而言，锗烯的霍尔效应在常温下更便于观察。所以可以在理论上对锗烯的性质进行推导，使之在未来的生产中少走很多弯路。

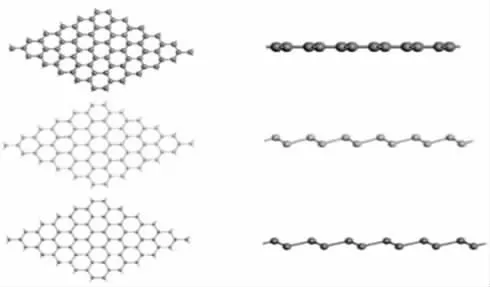
图2 左图为石墨烯、硅烯和锗烯的俯视图，右图分别为其侧视图

由于锗烯中的原子在排列时形成了褶皱，这种结构使得锗烯电极材料在充放电的过程中依然能够保持稳定，同时还可以避免长时间使用后传统电极材料会出现膨胀的问题。目前，锗烯的应用已经使得超级电容器的性能得到了极大的提升，在新能源汽车等领域已经得到了一定的应用。

3 基本理论和计算方法

3.1 第一性原理

第一性原理是一种通过大量的计算来求解薛定谔方程的方法。在运算的过程中，要以原子核与电子的相互运动规律为主，结合量子力学中相关的原理与方法。对于一个多粒子体系而言，求解薛定谔方程就在于如何获得它的本征函数与本征值。公式(1)为多粒子体系的薛定谔方程：

理论上，只要成功求解薛定谔方程，就能够通过本征函数与本征值去探讨一些基本的物理性质，然而电子之间存在非常复杂的作用力，通过求解薛定谔方程得到的结果往往不符合实际。当系统内部的原子数相对较少时，可以用Hartree-Fock 方法对其进行近似。但是，在系统内部的原子数比较多的情况下，计算量也将成倍增加，这对于计算机的运算力要求也非常之高，尤其在计算半导体等材料的能带时，误差往往比较大。为了能使计算结果与实际相符合，运算方法要继续升级，因此密度泛函理论应运而生。

3.2 密度泛函理论

对于多电子体系的薛定谔方程，通过Hartree-Fock(HF)方法近似是可以使方程更加优化的，但是从本质上讲，该方法仍然是基于电子波函数对方程进行求解。随着体系中电子数量的增加，波函数的数量也逐渐增加，因此求解薛定谔方程的运算变得越来越困难，限制了该方法在实际中较大体系下的应用。但是从科研需要出发，求解薛定谔方程的方法需要不断地革新，直至二十世纪六十年代，Kohn、Hohenberg 和Sham 三人提出了密度泛函理论。密度泛函理论的核心思想是：求解多粒子体系的薛定谔方程的本征函数与本征值时，把电子密度分布作为基本变量，从而得到体系的基态性质。

3.2.1 Kohn-Hohenberg 定理

密度泛函理论的基础来自Kohn 和Hohenberg 提出的“固体的基态性质可以用电子密度来描述”，在均匀电子气模型应用Kohn-Hohenberg 理论，包含以下两个定理：

定理一：任意一个忽略自旋的电子体系内，基态分子的电子密度都可以唯一决定该体系的基态能量和其他电子性质。即

3.2.2 Kohn-Sham 方程

通过结合物理学中的变分原理可知，体系的能量泛函的实际取值在KS 轨道作用下能够得到最小值。优化后得到以下方程：

KS 轨道是为了计算电子密度而引入的、建立在假想参考系上的轨道，可以发现，KS 轨道与HF 轨道非常相似，即使KS 轨道并不满足与Koopmans 的近似，但KS 轨道仍然可以得到一些有用的结果，例如分析分子的性质。一旦确定了体系的交换关联能，就可以应用(4)的自洽，最终精确求解真实体系的基态能量和粒子密度。

3.2.3 交换关联泛函

在求解方程(4)的过程中，核心在于交换关联泛函如何给出，但是由于很难用常规的公式表达出交换关联泛函，在以往的研究过程中，科研工作者们采用了一些近似，包括但不限于对关联函数的对称性和归一化等参数做出限定，最终给出了交换关联泛函的近似表达式。

在处理关联项时，最为熟练的方法是局域密度近似，其基本思想类似积分，将不均匀的电子气不断拆分，直至拆分成无数个无穷小的体积元，不均匀电子气即可看做无数局域均匀的电子气的迭加，最终通过对均匀电子气的交换关联项进行积分，就可以得到整个体系的交换关联能。实际应用中，还要考虑到电子的自旋，交换关联函最终写为：

采用LDA 计算以强键结合的晶体固体材料时，得到的理论值基本符合实验结果，但在计算以弱键结合的体系时，理论结果得到的键长以及半导体材料的带隙值通常比实验值低很多。

在计算交换关联能是还会采用到广义梯度近似，这种近似方法的基本思想是，在计算结晶固体材料的物理性质时，采用电子密度和电子密度梯度为基本变量。在GGA 情况下，电子密度和电子密度梯度的泛函就是交换关联能，表示成数学形式：

显然，GGA 对交换关联能的计算精度要比LDA 更高一些。

3.3 态密度和能带结构

在分子的形成过程中，由于原子轨道之间的作用形成了具有分立能级的分子轨道。而晶体这种物理性质稳定的特殊固体材料，就是由大量的原子通过有序堆积形成的，所以在微观的角度上，大量具有分立能级的分子轨道也被有序堆叠，这些被堆叠的分子轨道的能级呈现出准连续的一条带，物理学中将它称为能带。

能带结构作为目前采用第一性原理能够计算得出的最常用的信息，能够为接下来的计算做出一定的准备。能带结构分为价带、导带和禁带，如图3 所示，如果导带和价带之间分立，则称这条空隙称为能隙，用Eg表示。

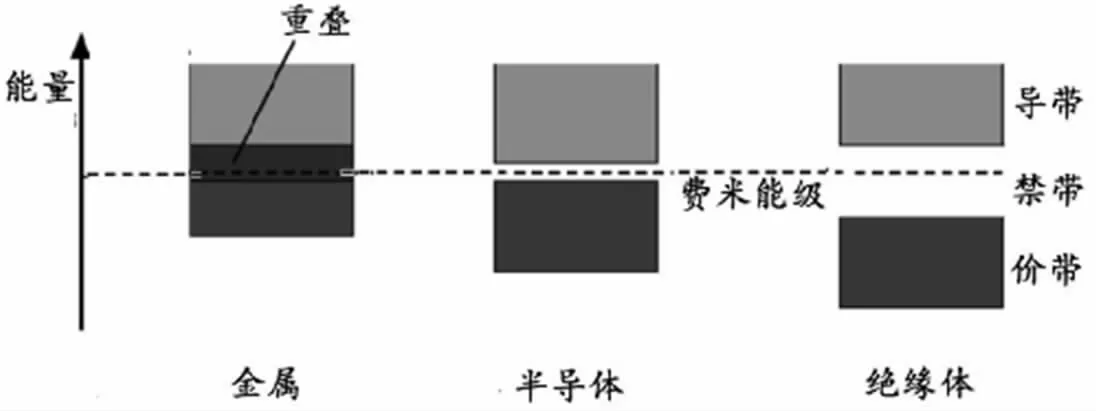
图3 固体的能带结构

在软件中，通过分析能带结构可以得到一个有规律的结果，称之为态密度。态密度和能带结构之间存在着许多共性，大部分术语也都是彼此相通的。但由于态密度呈现的结果更为直观，因此在结果讨论中比能带分析更加适用。电子能级在不断地堆叠呈现准连续分布形成能带时，单位能量间隔内总的电子态数目就称为态密度，也可以表示为，量子态数目△Z（介于E～E+△E 之间）与能量差△E 之比。态密度可以决定固体的大部分光电学性质，材料对X 射线的吸收与发射能力正是由态密度所决定的。

总而言之，分析态密度与能带结构都是用于探究固体的结构性质的手段，通过这些理论上的计算可以很好的预测材料的性质，或者用理论与解释实验上的现象。

4 理论计算

本文采用VASP 软件包、基于密度泛函理论的缀加投影波法来计算金属原子掺杂锗烯材料的量子电容，彼此相互作用的电 子 交 换 关 联 能 采 用 广 义 梯 度 近 似 下 的Perdew-Burke-Ernzerhof(PBE)泛函。为确保总能量收敛达到1 meV/atom，将K 点的截止能设置为450 eV，计算将自旋考虑在内。

本文构建了锗烯的单层4×4 大小的超胞结构。通过单空位锗烯上吸附Au、Ag、Cu、Al、Ti 金属原子，期望提升锗烯基材料的量子电容。图4(a)为金属原子在锗烯结构上可能的吸附位，(b) 为单空位锗烯，通过计算发现，Al 最稳定的吸附位在Valley位置，Au、Ag、Cu、Ti 最稳定的吸附位在Hollow 位置。

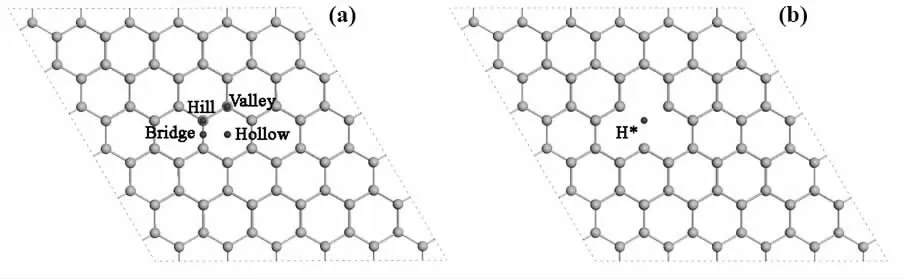
图4

5 结论

本文通过研究锗烯的电子结构来不断提升其量子电容。通过计算、研究单空位锗烯在不同原子掺杂下的性质，发现这些金属原子是以嵌入空位的形式吸附的，因此会在空位形成很强的化学键，使得锗烯在某些性质上表现出了准金属的特点。通过研究发现Au、Ag、Cu、Al、Ti 原子吸附单空位锗烯的量子电容明显增加，原因是这些原子的吸附明显调制了费米能级附近的态密度。通过对比，其中Ti 原子吸附单空位锗烯对量子电容的改善最大。根据公式1/CT=1/CD+1/CQ，提高量子电容，可以进一步提升总界面电容，从而提高超级电容器的能量密度。