多相流流动对管道腐蚀状况研究
张洋洋,刘志慧,耿光伟,张鲁飞
(中国石油大学(华东)石油工程学院,山东 青岛 266580)
伴随油气田开采进程,产出气含水率逐渐升高,同时气中含有CO2生成碳酸[1-3],形成多相流的交变侵蚀,对油管具有极强的腐蚀性[4-5],严重影响着实际生产。因此,明确多相流对油管腐蚀的影响,预测油管腐蚀发展规律及速率特性对管道的维护、治理达到二次应用具有重要指导意义。
国内外学者对多相流流动及管道腐蚀分别做了大量的研究,主要表现为流型变化机理划分依据,温度、压力、流体介质等方面对管道腐蚀的影响,但对于管道腐蚀速率与多相流状态关系的综合研究较少。Taitel、Shoham[6]利用有限元的方法,离散分析气液两相流型的变化过程。Ramdin Henkes[7]采用FLUENT软件模拟计算竖直管道内泰勒泡的运动过程,并分析管道内部气泡的影响因素。Kosterin[8]提出流型图的概念,根据该理论可以判断流体的结构特征;Baker[9]在前者研究基础上进一步改进了流型判断方法。Hilliard H M[10]认为腐蚀管道的主要原因是CO2分压、流速、温度等;1983年Crolet,Jean-Louis[11]等人在前人成果基础上又探索流动条件和腐蚀的关系;任呈强[12]等人认为CO2和H2O两种介质对管道腐蚀有重要影响;Fierro G(1989)、Dugstad A(1994)、Ma Houyi(2003)等人进一步探讨管道腐蚀影响因素;2013年Jepson发现了流型的变化对于腐蚀有重要影响。
文章基于FLUENT-OLGA软件,结合某气田开发工程背景,在Jepson的研究基础上通过数值模拟流相分布特性及腐蚀发展规律进一步研究多相流流动对管道腐蚀速率的影响。
1 控制方程
管道内部流动比较简单,内部流场没有运动构件干扰,无强湍流状态。流体流动均遵循能量守恒、动量守恒和质量守恒方程:
(1)
式中:ρ——流体密度,kg/m3;φ——通量变量;Γ为扩散系数;S——源项。
管内流动属于非稳态湍流运动,可采用k-ε模型预测不同流相运动轨迹。
k方程:
(2)
ε方程:
(3)
式中:k、ε——湍流动能和耗散率;μ——动力粘度;μt——湍流粘度;σε、σk——耗散率和湍流动能对应的普朗特数;Gb、Gk——由浮力影响和平均速度梯度产生的湍流动能[13];Sk、Sε——用户自定义源项;Cε1、Cε2、Cε3——经验常数。
VOF方法来追踪气—液两相自由界面。第q项流体在控制体内的流体体积分数函数Fq满足如下方程和控制条件:
(4)
∑Fq=1
(5)
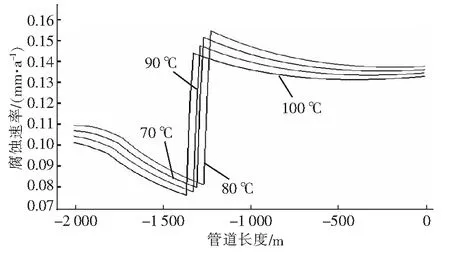
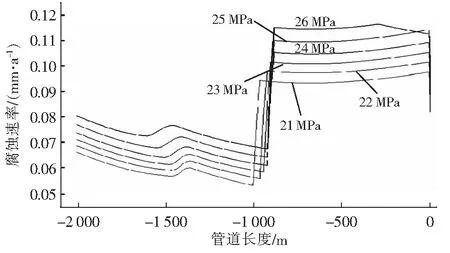
式中:u,v——在x,y方向的速度分量,m/s;Fq——第q种物质在单元格中所在体积分数,Fq=0,表示单元格中没有此相,Fq=1表示充满,在交界面上0 VOF方法中,流体物性参数由控制体单元内各相物性参数共同决定,表达式为: φ=∑φqFq (6) 管道的几何模型较为简单,简化示意图如图1。管道内径0.082 4 m,管长9 m,管道内部气相、水相从井底部自下往上流动,模拟过程中存在壁面黏附作用。严格意义上,仿真模拟管内多相流流动采用三维模型更贴近实际工程,但对于网格划分、迭代收敛时间的要求,加上气、液两相在管道内部许多参数是不相等的,因此按照三元问题去解决又存在一定的局限性,文章选用二维流场模拟。管道材料属性如表1。 图1 几何示意图Fig.1 Geometric diagram 表1 管道参数Tab.1 Pipe parameters 对所建几何模型做以下简化:(1)气田现场油管较长,为方便计算,将管道长度取短;(2)井筒中流体的特点,表现形式为不可压缩;(3)模拟过程中热交换为零,保证恒温恒压;(4)忽略流体与壁面的粘性力。 在二维网格划分过程中,考虑到管壁面的粘附作用,在壁面适当添加边界层,并对井底和井口进行适当的网格加密,网格划分如图2。 图2 计算网格划分Fig.2 Computational meshing 相态的设置中以气体作为主相,液态水作为第二相。流相的物理性质表如表2,数值模拟过程中,液相和气相同时从井筒管道底部向上流动,底部设置为流量入口,井口设置为压力出口。 表2 气液两相流体的物性组成Tab.2 Physical composition of gas-liquid two-phase fluid 液相和气相的相互流动为紊流,雷诺数,选择k-e模型;在确保收敛前提下,使用Second Order Upwind的离散方式,这种格式可以获得较精确的解[14-15],时间步长设置成2×10-5s。欧拉法将各不相同相态比作相互贯通的介质,主要包含VOF、Eulerian、Mixture[16-20],文章选择VOF方法。此次模拟基于实际工况的参考下,忽略凝析油的产量,将含水率直接定义为含液率,水的质量流量粗略当成液相质量流量。 考虑计算机的容量问题,为保证模拟结果的真实性,对网格进行无关性检验,定性分析气相在管道径向位置(x方向)上的体积数分布特性,根据图3计算可知,随着网格数的增加,气相流速精确度越高,网格数量在150 000~240 000区间内,计算结果相差无异,网格数110 000时,计算精度不满足要求,因此从计算耗时角度考虑,网格数量低迭代速度快,最终网格总数为160 000个,可以满足计算的精度要求。 图3 网格线无关性验证Fig.3 Verification of grid line independence 设置气相质量流量为1.7 kg/s,改变入口处含液率数值,模拟计算竖直向上的管内气液两相流型,得到不同工况下的气液两相分布云图。为便于观察,将管道自下而上分为a、b、c、d、e五段。当管内持液率为0.05%时,管内依次出现气泡流、离散气泡流等典型流型。各流型特征如图4。 图4 含液率0.05%的相分布云图Fig.4 Cloud diagram of phase distribution with liquid holdup of 0.05% a、b管段表现为气泡流。液相流速较小,气相流速较大,气相流体连续流动,液相以小液滴的形式分散其中。随着流体不断上升,从c管段开始,伴随气相带动液相向上流动过程,部分小液滴聚合形成大液滴,聚集在管壁附近,形成离散气泡流,管内流型主要呈现气泡流的形式。 持液率增至0.09%,如图5。管内依次出现分层流、气泡流、离散气泡流、搅混流及环状流等几种典型流型。a管段底部出现分层流,液相与气相相界面光滑,分层明显。离散小液滴在气相带动下不断向上运动呈现气泡流状态;b管段小液滴杂乱运动,不断聚合、破碎形成离散气泡流;c、d管段气相和液相主要分布在管内中心位置,两相界面不规则,整个流动为搅混流;在e管段以上,发现在壁面附着一层液膜,中部为气相分布,气相会夹杂小液滴。 图5 含液率0.09%的相分布云图Fig.5 Cloud diagram of phase distribution with liquid holdup of 0.09% 持液率增至0.11%,管内流型主要为弹状流,如图6,包含有段塞流、环状流、气泡流、分层流等典型流型。底部分层流较为明显,液相分离出小水滴,形成气泡流。液滴与气相不断碰撞,气液相界面不规则,呈现搅混流。壁面出现规整液膜,同时伴有大量气泡或大液滴继续流动,管道中心位置流动紊乱,整体表现为环状流。伴随流动影响及重力作用,离散液滴聚合生长成为大水滴或水泡,如子弹头模式的弹状流,管内环状流—弹状流交替出现。 图6 含液率0.11%相分布云图Fig.6 Cloud diagram of phase distribution with liquid holdup of 0.11% 持液率增至0.16%,在管道底部几乎充满流体,液相流量不断增多,随着流体不断向上移动,气液两相边界逐渐清晰可见,虽然比较混乱,但依然可以看到大气泡,即为泰勒泡,这时管道流型主要呈现段塞流形式,如图7。 图7 含液率0.16%相分布云图Fig.7 Cloud diagram of phase distribution with liquid holdup of 0.16% 表3是通过FLUENT模拟计算得到的不同质量流量下的流型分布特性,利用OLGA软件来分析不同流型对管道腐蚀速率的影响。 由表3可知,气液两相流动状态随液相质量流量变化而变化,先后有气泡流、环状流、段塞流等流型出现,与之前Fluent模拟计算基本吻合。流型的种类繁多,不止包括以上这几种,对于流型的分类只能粗略的划分,通过计算云图可以很清晰的观察到管道内部流型的分布情况。 表3 不同质量流量下的流型分布Tab.3 Flow pattern distribution under different mass flow 当温度不变时,管道腐蚀程度沿井筒方向降低;小于80 ℃,进口温度不断升高,管道破坏逐渐增大;高于80 ℃,进口温度不断升高,腐蚀程度呈现降低趋势。综上,管道腐蚀速率先增大后减小,此时以局部腐蚀最为严重,温度变化对壁面腐蚀有影响较大。 图8中纵坐标数值2、3分别代表环状流和段塞流的分布状态。温度不同,对应的管内流型分布大致相同,温度变化对于内部流型的改变影响不大。 不论温度高低,井口位置腐蚀都远远高于井底位置腐蚀,对比发现:当流型为环状流时,其腐蚀速率远远低于段塞流时的腐蚀速率,且在流型转变位置,壁面腐蚀速率发生较大变化,反映出在不同温度条件下,流型的变化对于壁面腐蚀程度起到很大的影响。 图8 流型和腐蚀速率的关系Fig.8 Relationship between flow pattern and corrosion rate 图9为不同压力条件下,流型沿管道的分布情况,分析可知:随着压力的变化,管内流型的变化趋势不大。管口四周区域多为段塞流,管道底部四周多为环状流。随着压力越来越小,环状流覆盖范围增多,段塞流覆盖范围减少。综合分析,不同压力对应的流型分布大致相同,压力变化对于管道内部流型的改变影响较小。 图9 管道流型分布Fig.9 Distribution of pipeline flow pattern 图10为不同进口压力条件下,壁面腐蚀程度沿管道的分布情况。管道底部压力不断增大,其腐蚀程度也相应逐渐增大。同一压力条件下,管道在井底腐蚀较为严重;靠近管口位置,破坏性比较显著,且井口破坏程度远大于井底。 图10 管道腐蚀速率分布Fig.10 Corrosion rate distribution of pipeline 对壁面侵蚀破坏作用最强的是段塞流,平均腐蚀速率为0.21 mm/a;其次为环状流,平均腐蚀速率为0.18 mm/a。同时随着压力的增大,流体速度增大的位置越趋向于管口位置,导致此位置发生流型的转变,从而使得壁面腐蚀速率发生巨变。这表示随压力不同条件,流型的变化对管道腐蚀程度有重要影响。 文章在Jepson的研究基础上基于FLUENT-OLGA数值模拟流相分布特性及腐蚀发展规律进一步分析流型对管道腐蚀速率的影响。 1)通过模拟计算直观的解释气液两相流流型变化规律,引起流型转变的本质原因是液率的变化。 2)管内压力、温度对管壁腐蚀影响很大,同时管内流型转变的存在加剧了管壁腐蚀程度。环状流腐蚀速度低于段塞流,在流型改变的位置,壁面的腐蚀速率发生巨变,反映流型变化对壁面腐蚀程度的影响。 3)段塞流对管道壁面腐蚀最严重,其次为环状流,气泡流的腐蚀程度表较弱。此外,在计算过程中发现液相流速和壁面剪切力的变化对腐蚀存在一定影响,也是下一步的主要研究方向。2 计算模型
2.1 几何模型简化


2.2 网格划分及边界条件


2.3 网格无关性验证
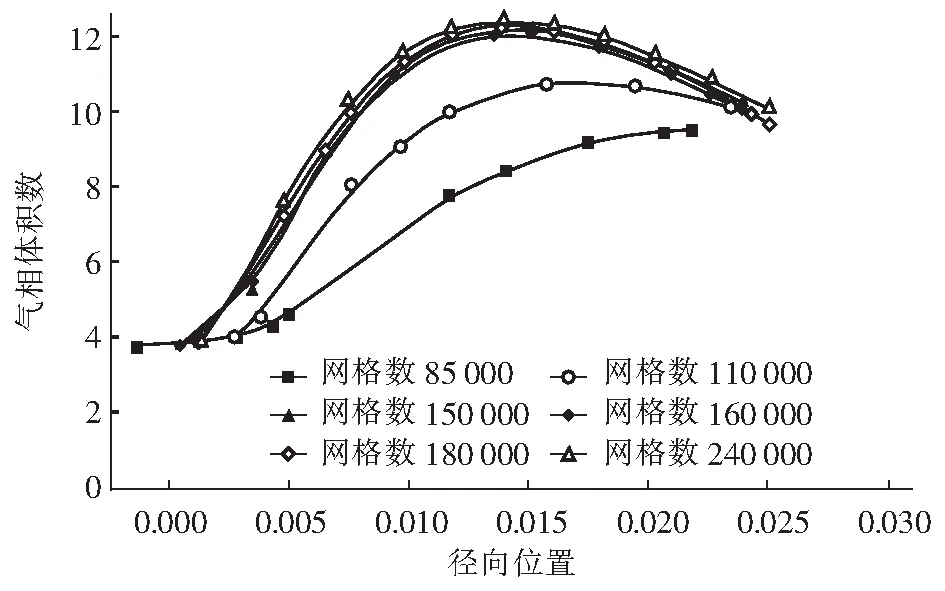
3 计算流态分析
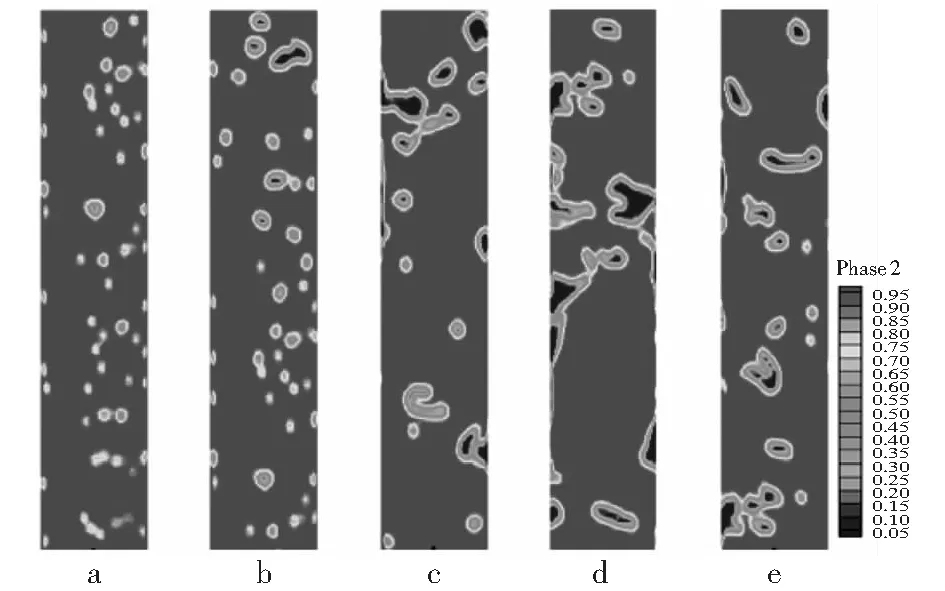
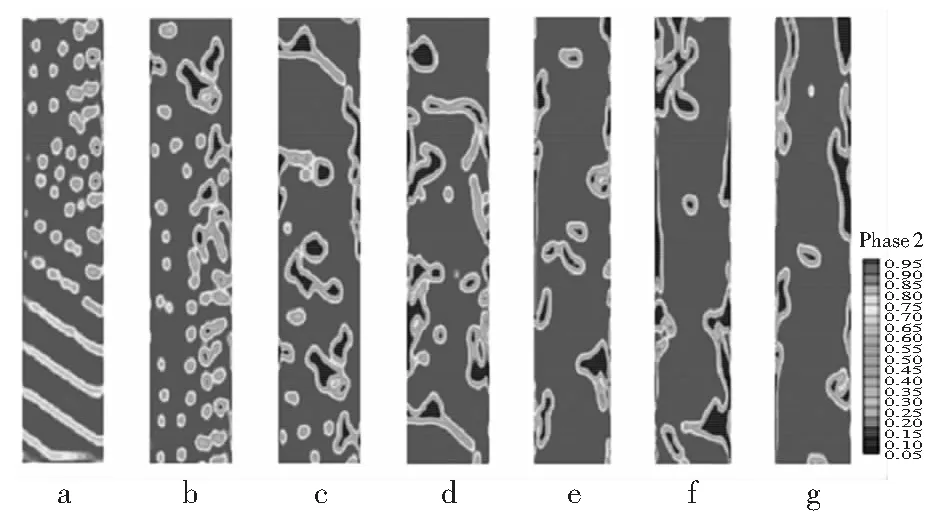


4 不同流型的腐蚀分析
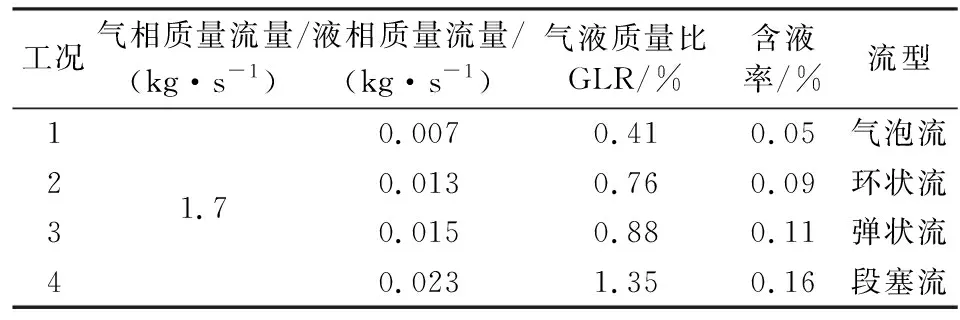



5 结论

