离散支承梁分段动力学建模方法

吴浩慜，邵济明，卢 健，王 熙，杨斌堂

（1.上海交通大学 机械系统与振动国家重点实验室，上海 200240；2.上海宇航系统工程研究所，上海 201109； 3.西南交通大学 机械工程学院，成都 610031）

近年来，随着运营里程数的不断增加，轨道交通逐渐成为诸多城市上班族首选的出行方式。然而，城市轨道交通在给市民带来交通便捷的同时其自身伴随的结构振动与噪声污染也会对沿线住户的日常生活造成影响。为了更准确分析轨道交通振动与噪声的成因以及传播机理，专家学者们通过构建车辆-轨道耦合动力学模型来模拟移动载荷作用下全系统的动力学响应，以此来寻求对于振动与噪声的抑制手段。其中，轨道结构振动方程作为模型中的重要组成环节，其求解方法对于模型的计算精度有着直接影响。

上个世纪下半叶，国外较早展开了轨道动力学的理论研究。Ono 等[1]从理论上分析了在车轮施加的移动冲击载荷和轮轨表面粗糙度共同作用下钢轨的动力学响应。Jezequel[2]将轨道简化为弹性基础上的无限长Euler梁，并引入旋转刚度描述梁的剪切效应，该模型结合波动方程可以计算出周期性结构在移动载荷下的临界速度。Timoshenko 等[3]采用Lagrange法求解了连续弹性支承梁的自由和受迫振动响应，对比两者的计算结果发现梁在简谐力作用下的动挠度可以由恒力载荷作用下的静挠度导出。相比于国外，国内在上世纪90年代后才开始车辆-轨道耦合动力学领域的理论研究，起步较晚。1992年，翟婉明[4]首次将轨道、车辆动力学以及轮轨间相互作用当作一个总体系统进行考察，建立了车辆-轨道垂向统一模型。徐志胜等[5]在上述理论的基础上建立了基于Timoshenko梁的车辆-轨道耦合振动模型，探究1 000 Hz以上中高频段内剪切变形对轨道加速度的影响。Wu[6]基于轮轨-减振器系统动力学模型、滚动接触力学和摩擦学，模拟了钢轨波磨的生长过程，发现轨道减振器的引入可有效抑制pinned-pinned共振引起的短节距钢轨波磨的生长。

然而，上述研究在通过模态叠加法求解轨道动力学响应的过程中都对振型函数进行了简化。Wu[6]在计算轮轨-吸振器系统波磨生长的过程中，将简支梁的各阶振型作为基函数代入轨道竖直方向的振动运动微分方程，并依靠振型正交性求解出轨道在安装吸振器后钢轨波磨生长速度的变化；翟婉明[7]在其所构建的车辆-轨道耦合动力学模型中，将各离散轨枕提供的支反力视作外力项，在采用Rayleigh-Ritz法求解振动微分方程时，同样直接引入简化简支梁振型作为解的基底，该种简化方法只有当轨道计算长度足够长时才能获得令人满意的近似效果[8-9]。然而，当计算长度不足、周期支承特性缺失时，仍将轨道视作有限长简支梁得到的振型函数则不能充分表征轨枕的离散支承特性，实际工况下，弹性元件的引入会改变轨道的局部振型及固有频率。

针对一般离散支承梁，本文提出了一种分段建模方法，以n个离散支承为节点将简支梁分为n+1段，通过边界条件把支承约束作为弹性元件纳入模型中，而不是作为外力项，从而求解出更符合实际的修正振型函数以及固有频率。进一步，对比动力学建模与有限元仿真结果验证了本文所提出建模方法在其适用范围内的精确性和有效性，并给出不同支承刚度、计算长度下离散支承梁振型和固有频率的变化规律。

1 有限长离散支承梁分段动力学建模

有限长离散支承梁结构形如图1所示。假设梁为均质等截面梁，以i个离散支承为节点可以将简支梁分为i+1 段，每段梁横向自由振动的运动微分方程为：

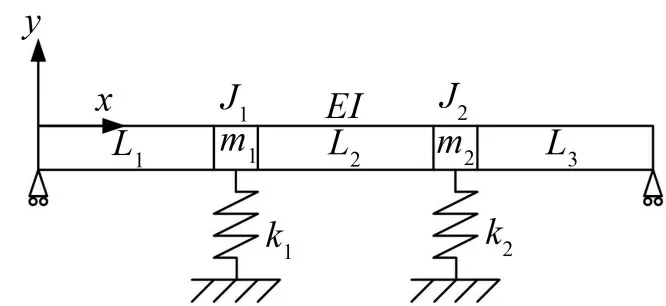
图1 有限长离散支承梁结构示意图

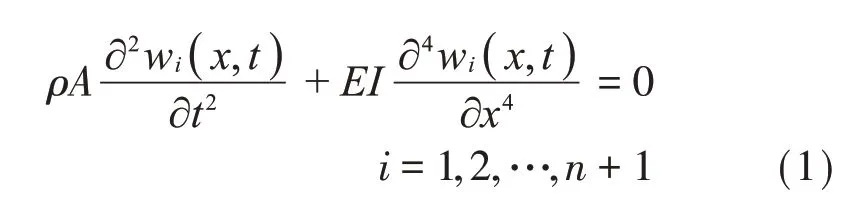
其中：wi(x,t) 为t时刻第i段梁上x位置处的横向位移；ρ为梁的材料密度；A为梁的横截面积；EI为梁截面的抗弯刚度。

为求解上述微分方程的解析解，这里采用分离变量法将2 元横向位移函数wi(x,t)写成振型Yi(x)与广义坐标qi(t)乘积的形式：

将式(2)代入式(1)，2 元4 阶微分方程解耦成只含振型Yi(x)与广义坐标qi(t)的2 阶与4 阶常系数线性齐次微分方程，可得两个方程的解具有如下形式[10]：

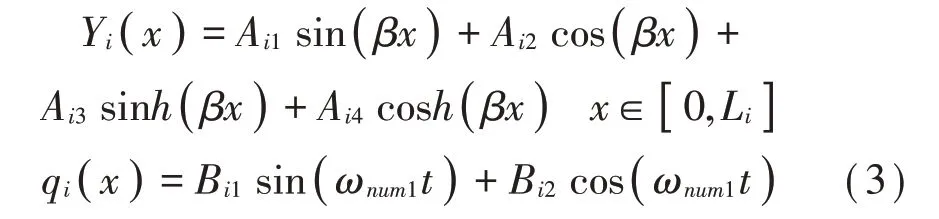
把式(3)写成向量乘积形式：

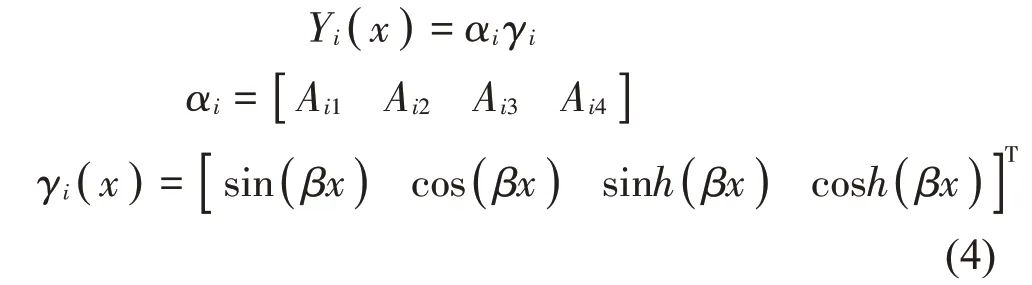
其中：ωnum1为整根梁的num1阶固有频率。

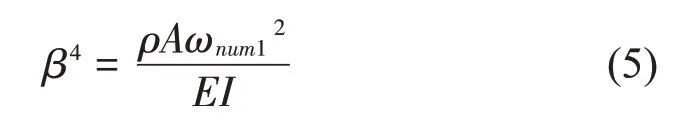
考虑到i+1 段梁有i+1 个振型函数，又每段振型函数包含4个独立的未知系数Ai1-4以及一个待求的公共未知数固有频率ωnum1，因此需要4i+4个边界条件以及行列式非零解条件才能够解出离散支承梁的num1阶振型Yi(x) 和固有频率ωnum1。下面将以图1所示包含两个离散支承的简支梁结构为例，给出各类边界条件的构建过程。

(1)简支端约束条件

根据简支定义可知，两侧简支端的位移和弯矩分别为零。

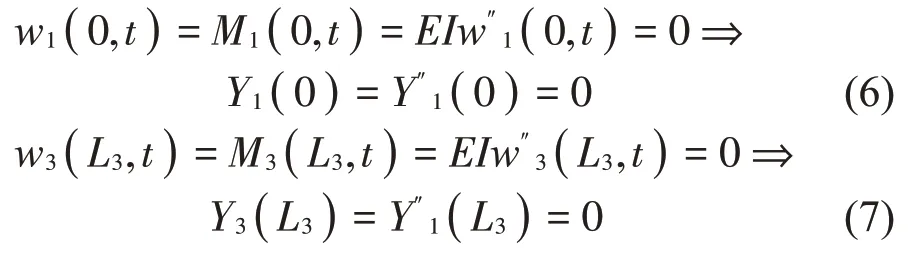
(2)连续性条件

由于离散支承梁为一连续系统，因此在第i段和第i+1段梁的连接处存在位移和转角相等的连续性条件。

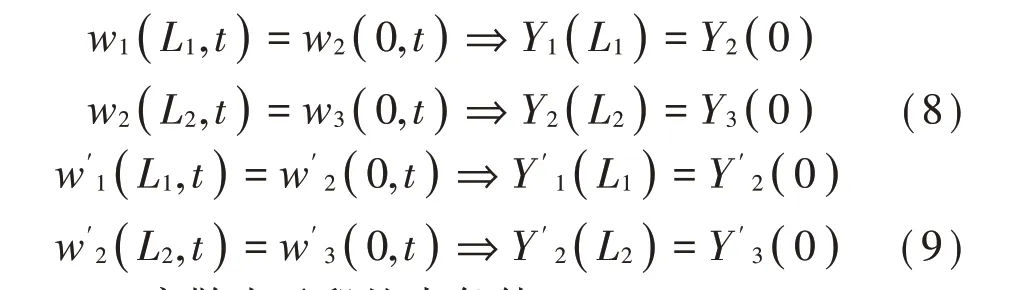
(3)离散支承段约束条件

如图1 所示。第i个离散支承处对应的短梁长度为ΔLi，且相比于两相邻离散支承之间的梁Li和Li+1，短梁由于长度较短、支承刚度较大可被近似视作刚体。结合图2，分别对短梁建立力和力矩平衡方程，即离散支承段的约束条件。

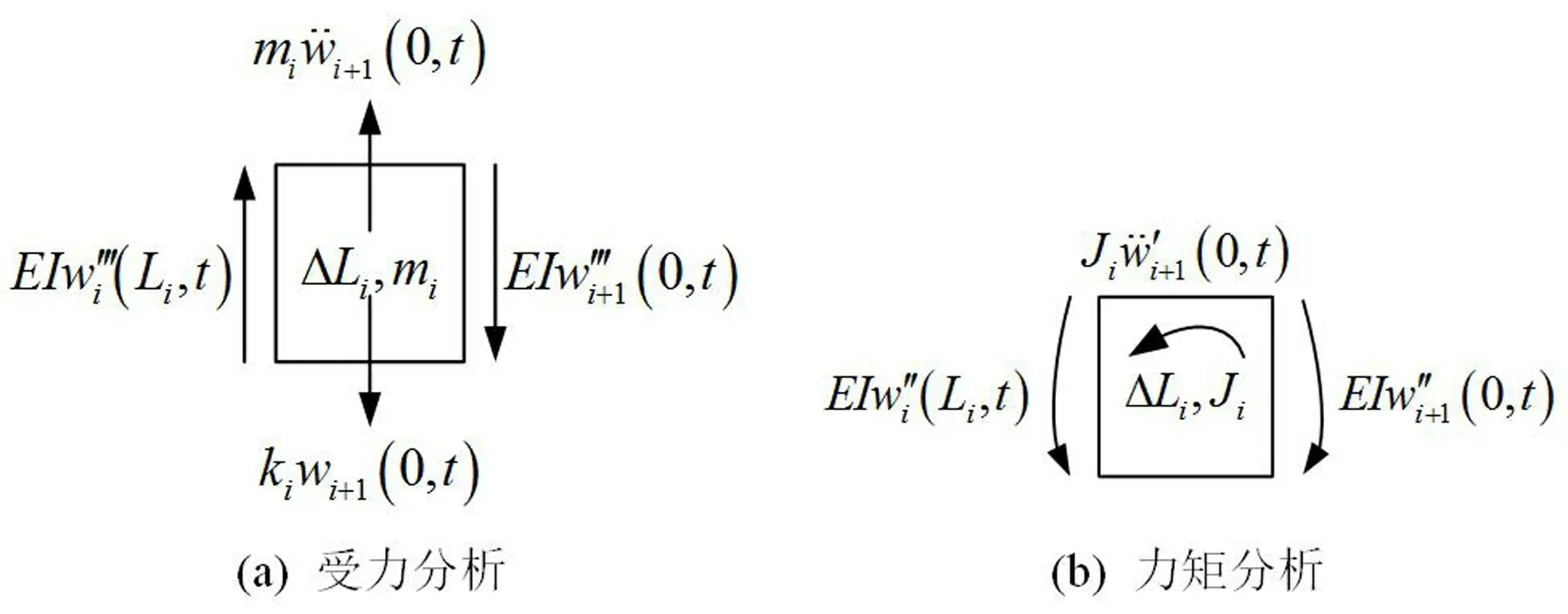
图2 离散支承段受力和力矩分析

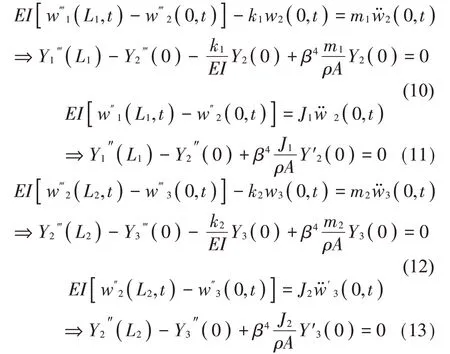
其中：mi和Ji分别为短梁的质量和转动惯量。

联立式（6）至式（13），可以得到12 个边界条件组成的十二元一次方程组的系数矩阵为G2，分别定义以下矩阵C至F：

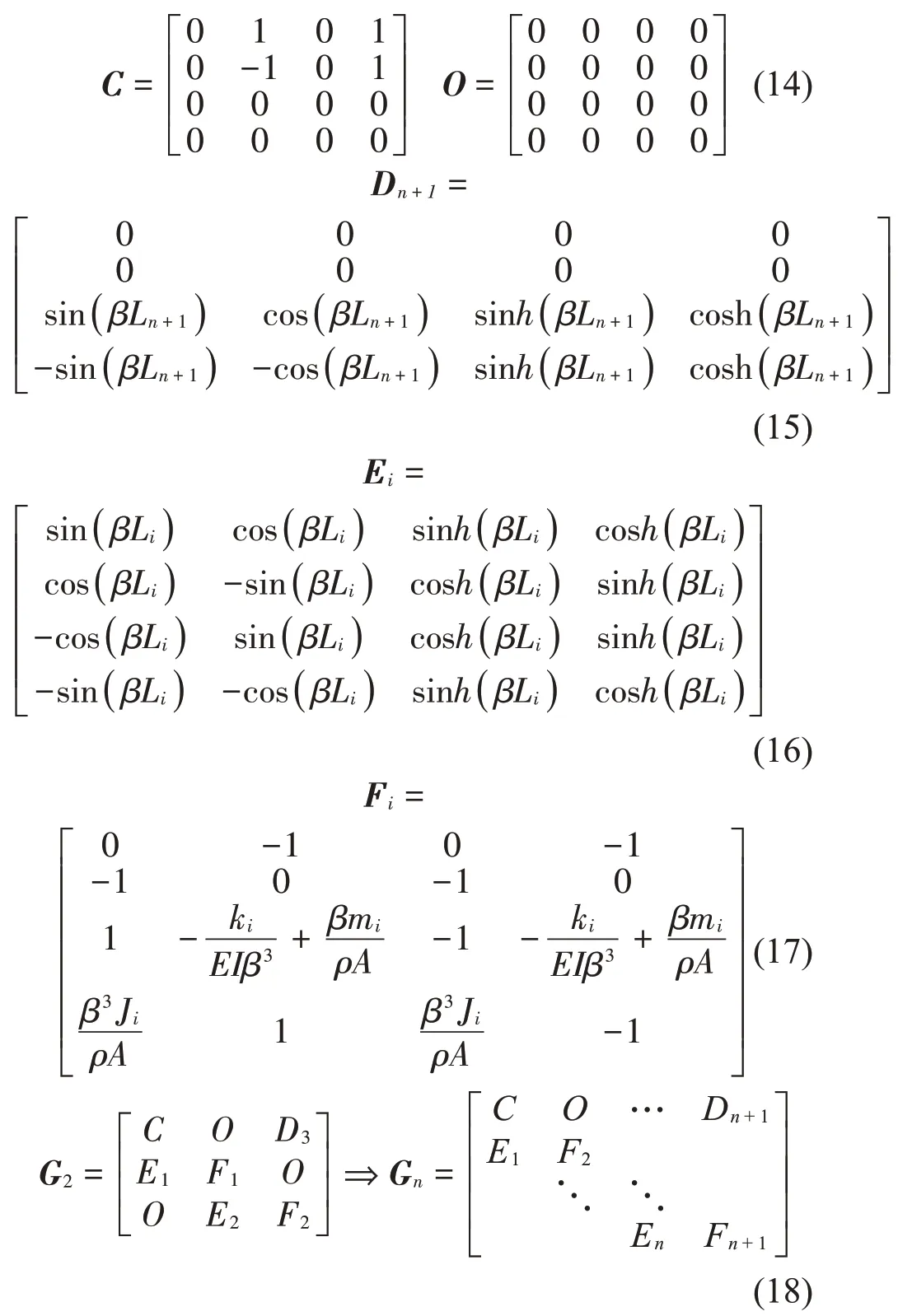
为了保证各段梁的广义坐标系数非零，包含n个离散支承的简支梁的固有频率ωnum1可以通过线性齐次方程组的非零解条件解得。

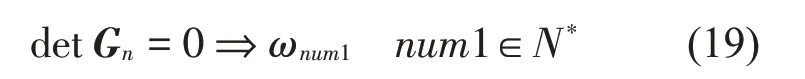
把固有频率ωnum1代回系数矩阵Gn后，通过高斯消元法求得方程组的基础解系，即第num1阶各段梁振型函数的系数矩阵Coff num1-n。

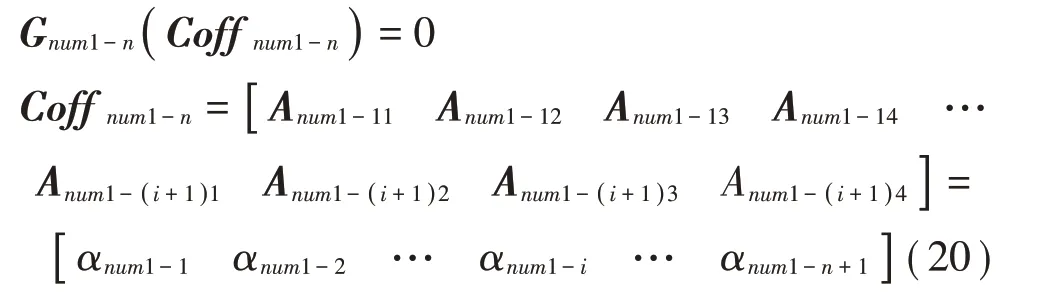
记取值函数Φ1-i(x)、Φ2-i(x)为：

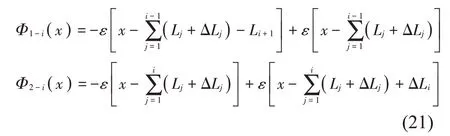
其中：ε为单位阶跃函数。

含n个离散支承的简支梁的第num1 阶修正振型函数Ynum1-n(x)为：

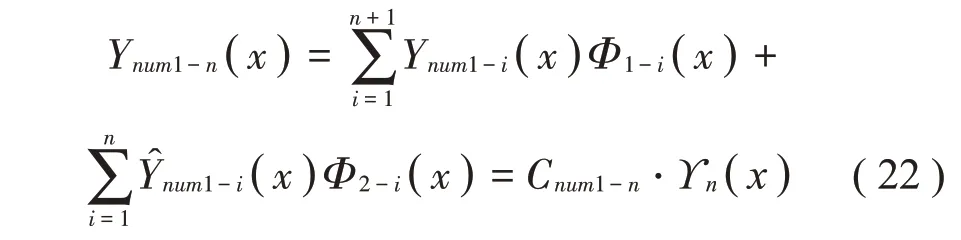
其中：

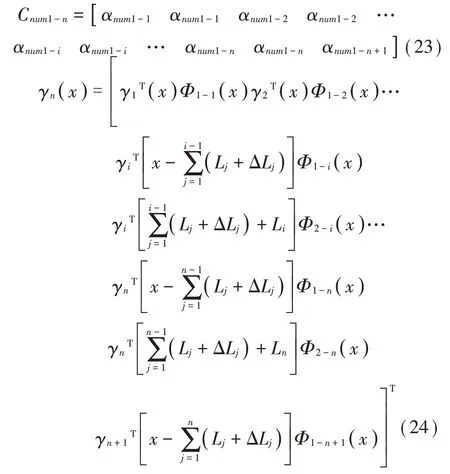
对Ynum1-n(x)进行归一化可得离散支承梁的第num1阶标准振型函数(x)：

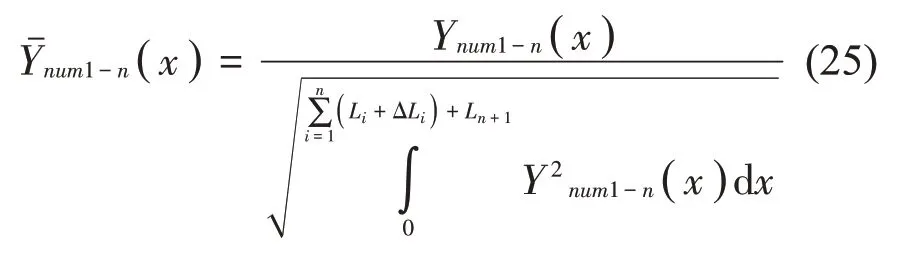
其中：

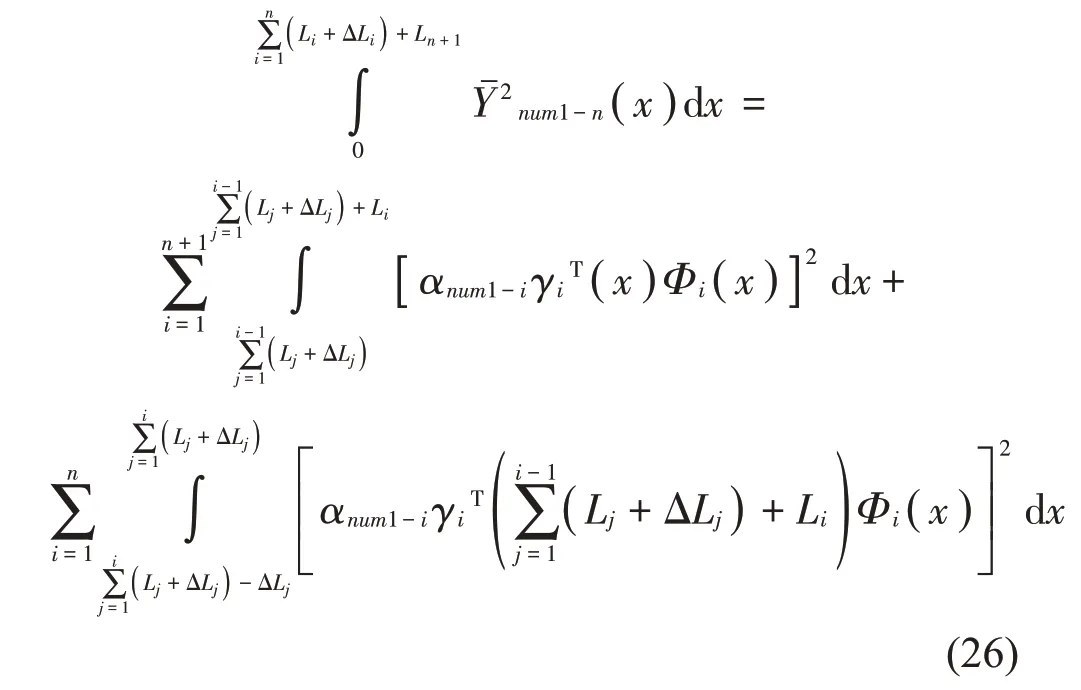
2 数值分析与仿真

2.1 可靠性分析（算例1）

为了验证所提出针对离散支承梁建模方法的可靠性，将数值分析计算结果（固有频率ωnum1）与有限元仿真结果进行对比，若两者对同一算例计算结果的相对误差小于3%，则可以认为所提出方法在适用范围内是可靠的。算例1 的结构示意图如图3 所示。主要尺寸及物性参数如表1所示。

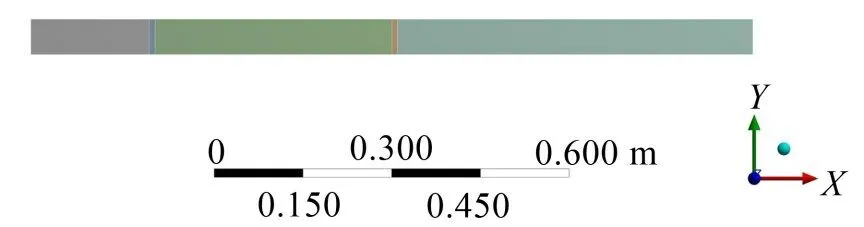
图3 算例1结构示意图

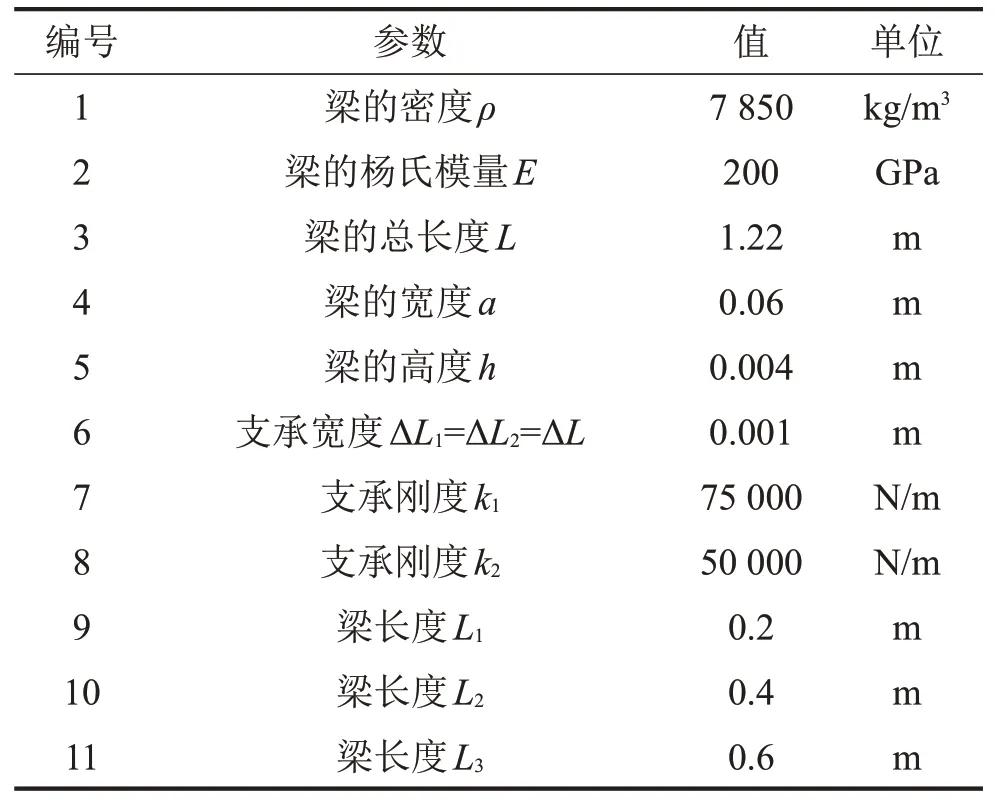
表1 算例1中主要尺寸及物性参数

其中，梁横截面对中心轴的极惯性矩I、支承座对应短梁段的质量mi以及转动惯量Ji可以由式（27）～式（29）计算得：

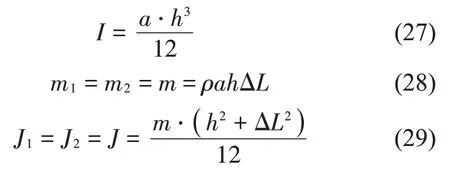
算例1 动力学建模与有限元分析结果即梁沿z轴方向的前10阶固有频率如表2所示。前4阶振型如图4所示。

如表2 所示。本文所提出建模方法对算例1 中离散支承梁沿z轴方向的前10阶固有频率的动力学分析结果与ANSYS有限元仿真结果较为接近，最大相对误差为2.91%，平均相对误差为1.24%，这说明针对有限离散支承梁的分段动力学建模方法是准确而可靠的。总体上，两种方法之间的相对误差随着模态阶数的增加而变大，其中相对误差出现波动的原因可归结为如下两点：

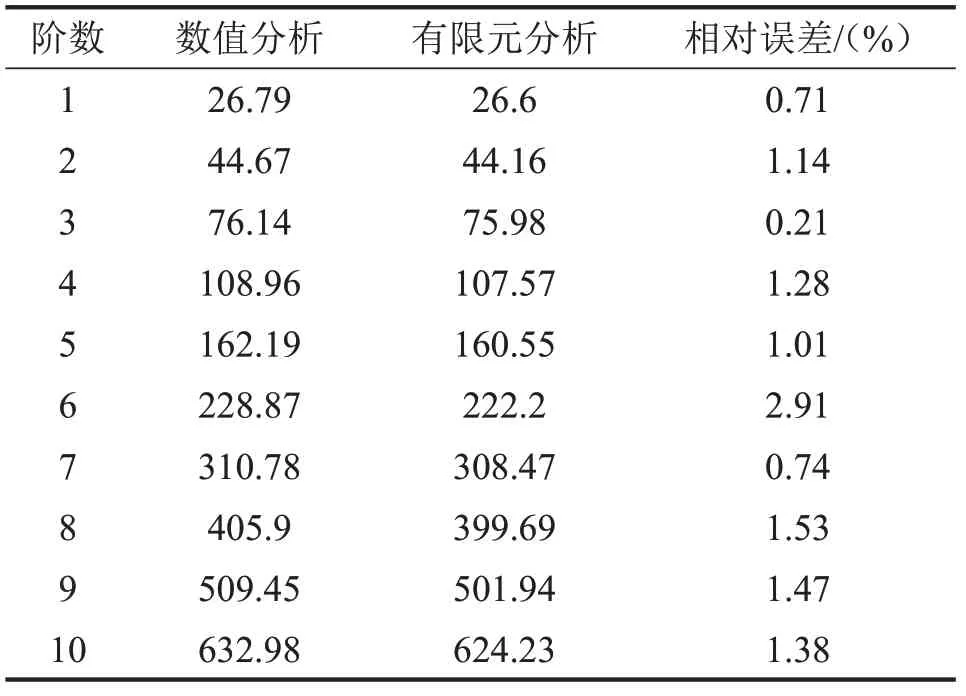
表2 算例1中固有频率计算结果/Hz

(1)由于三段梁(L1-L3)的长度不同致使每段梁所包含的有限元网格数随着长度的增加而增加，包含的网格数越多该段梁的计算精度越高；

(2)梁的长度增加，剪切变形影响减小，更加符合模型中的Euler梁假设。

以上两点解释了当离散支承梁的第num1 阶振型最大值出现在梁L1段内时，相对误差值会突然增大的现象。另外，如图4所示，引入两个离散支承后简支梁的前4 阶振型与原先的显然不一致，因此在使用模态叠加法求解外力作用下离散支承梁的动力学响应时就不能简单地把长度为L的简支梁的振型函数作为模态空间的基向量。

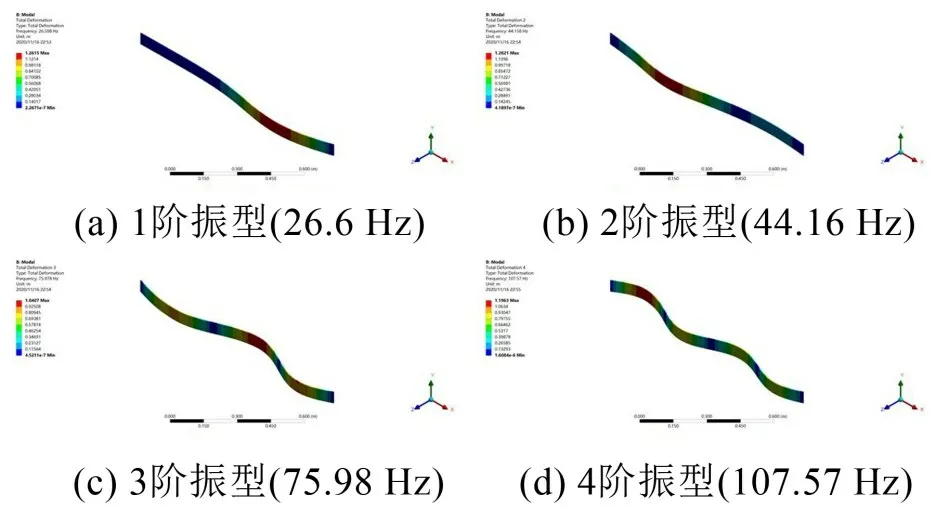
图4 非周期性离散支承梁的前4阶振型（算例1）

2.2 支承刚度（算例2）

考虑到支承刚度会随着梁与支承座之间弹性紧固件的型号、材料以及预紧力大小变化发生改变，算例2中相邻支承座间梁的长度(L1-L4)保持不变，仅改变支承刚度大小，观察离散支承梁前4 阶固有频率的变化。算例2 的结构示意图如图5 所示。主要尺寸及物性参数如表3所示。

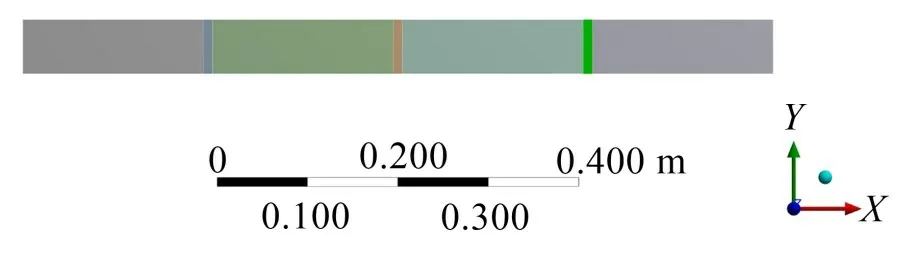
图5 算例2结构示意图

表3 算例2中主要尺寸及物性参数

对比表4 和图6 中算例2 的动力学建模和有限元分析结果可知，随着支承刚度k从0 增加至2 MN/m，离散支承梁的固有频率f1-3逐渐增加，且阶数越低增幅越大，相反，表4 中离散支承梁第4 阶固有频率f4的值几乎不发生改变，这是由于当支承刚度增加到一定程度后，支承处的弹性紧固件逐渐等价于固定约束，即被三等分后每段梁(L1-4)的f1等于原简支梁的f4，而f1-3则随着刚度增加逐渐逼近f4。另外，值得关注的是，f4的数值分析与有限元仿真结果相对误差达到了6.9%，其原因可能为：

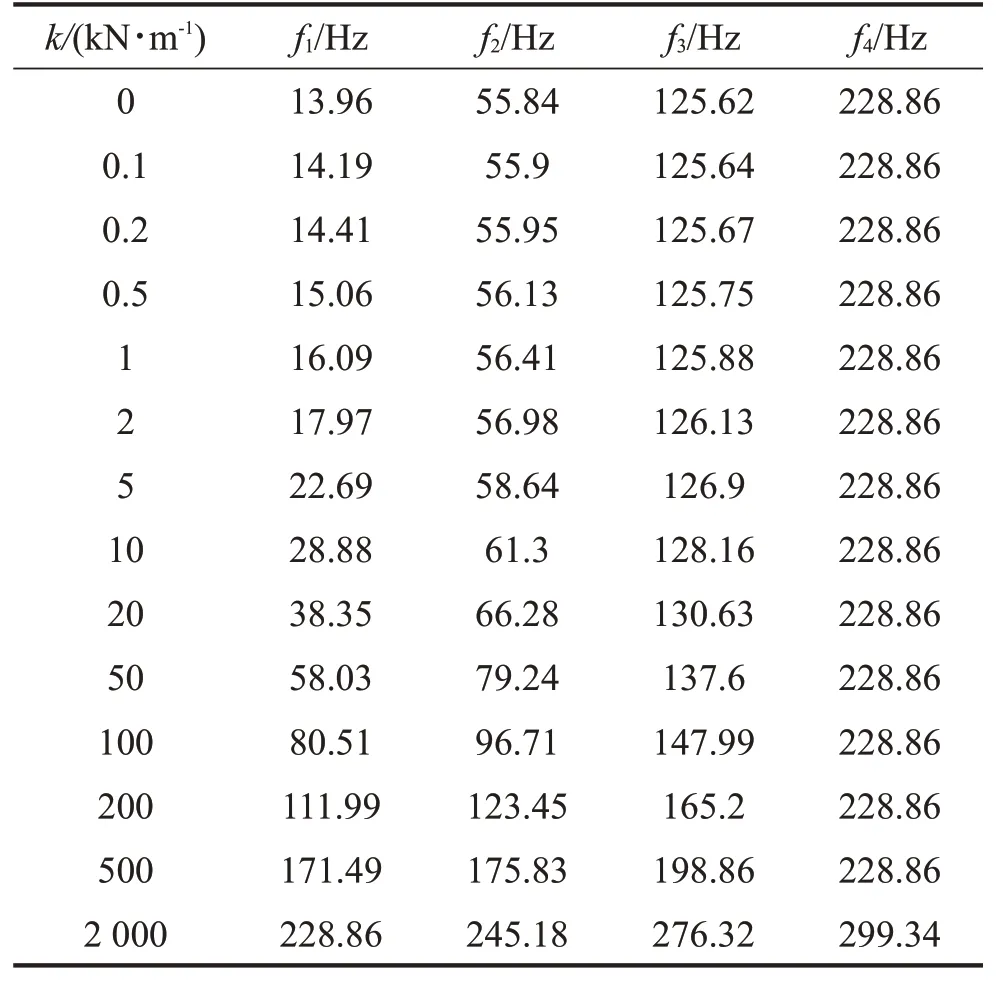
表4 算例2中不同支承刚度条件下梁前4阶固有频率计算结果

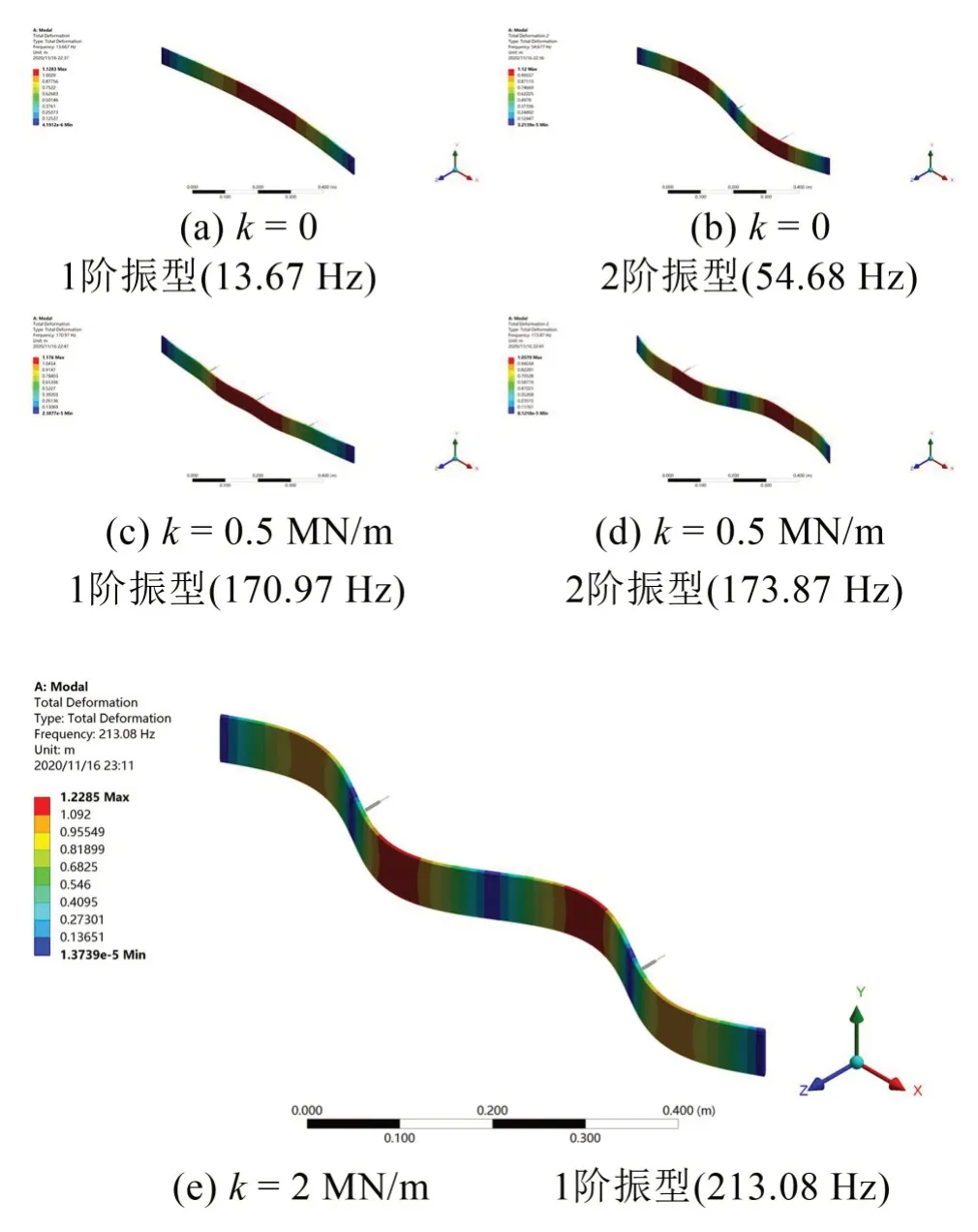
图6 不同支承刚度条件下周期性离散支承梁的前2阶振型（算例2）

(1)在有限元模型中支承段短梁被按六面体网格划分为若干单元，并不是刚体；

(2)随着支承刚度的增加，支承段短梁两侧连接处剪切变形和转动惯量的影响增大。

2.3 计算长度（算例3）

目前，车辆-轨道耦合动力学模型中通常采用的振型简化方法的使用前提有以下两点：

(1)支承梁具有对称性较高的周期性结构；

(2)离散支承梁的计算长度足够长。

为了进一步探究上述简化方法的适用范围，令ΔLi为一定值，并按单元段（两个离散支承之间的梁为一单元段）逐步增加计算长度。算例3 的主要尺寸及物性参数如表5所示。

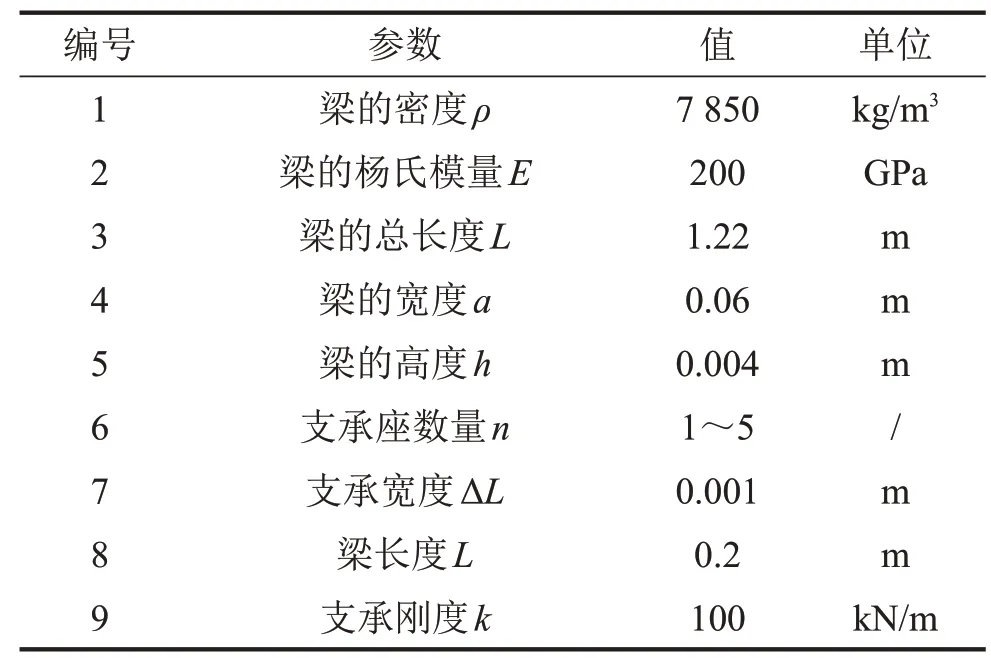
表5 算例3中主要尺寸及物性参数

一方面，从频率的角度（如表6所示）来看，随着计算长度的增加，周期性离散支承梁各阶固有频率的变化量逐渐减小，当计算长度趋向无穷时，各阶固有频率会收敛到一定值，另外，有趣的是随着n的增加，num1阶固有频率同样也会缓慢向num1-1阶靠近，最终趋向1阶固有频率，这也就是在车辆-轨道耦合动力学模型中存在最短计算长度的原因之一，且显然此时离散支承梁的固有频率远高于对应简支梁的。

表6 算例3中梁在不同支承座数量条件下250 Hz以下固有频率/Hz

另一方面，从振型的角度来看，当n=4、k=100 kN/m 时，对比简支梁与离散支承梁的1 阶振型函数（如图7 所示）发现，虽然两者的前两阶振型较为相似，但局部还是存在细微的差异，且经归一化后，通过分段建模得到的修正振型函数与ANSYS仿真结果几乎一致。当n=2,4,6,8 时，按式（30）计算上述两种方法得到1阶振型的误差，如表7所示。随着计算长度的增加误差逐渐减小，但降幅也同时减小，由此可以推断即使计算长度趋向无穷，两者之间的误差也不可能趋向零，因此采用分段建模方法得到的修正振型函数具有更高的计算精度，尤其是在以后采用模态叠加法求解轨道动力学响应时，每阶振型函数的误差会随着阶数的累积被不断放大。综上，针对算例3 这类周期性离散支承梁结构可以采用简化简支梁振型来近似，且近似程度随着计算长度的增加而增加，然而一旦离散支承梁结构在某一单元的参数发生变化，周期性遭到破坏，那振型上的近似特性也将不复存在。

表7 算例3中离散支承梁与对应简支梁1阶振型间的误差变化规律

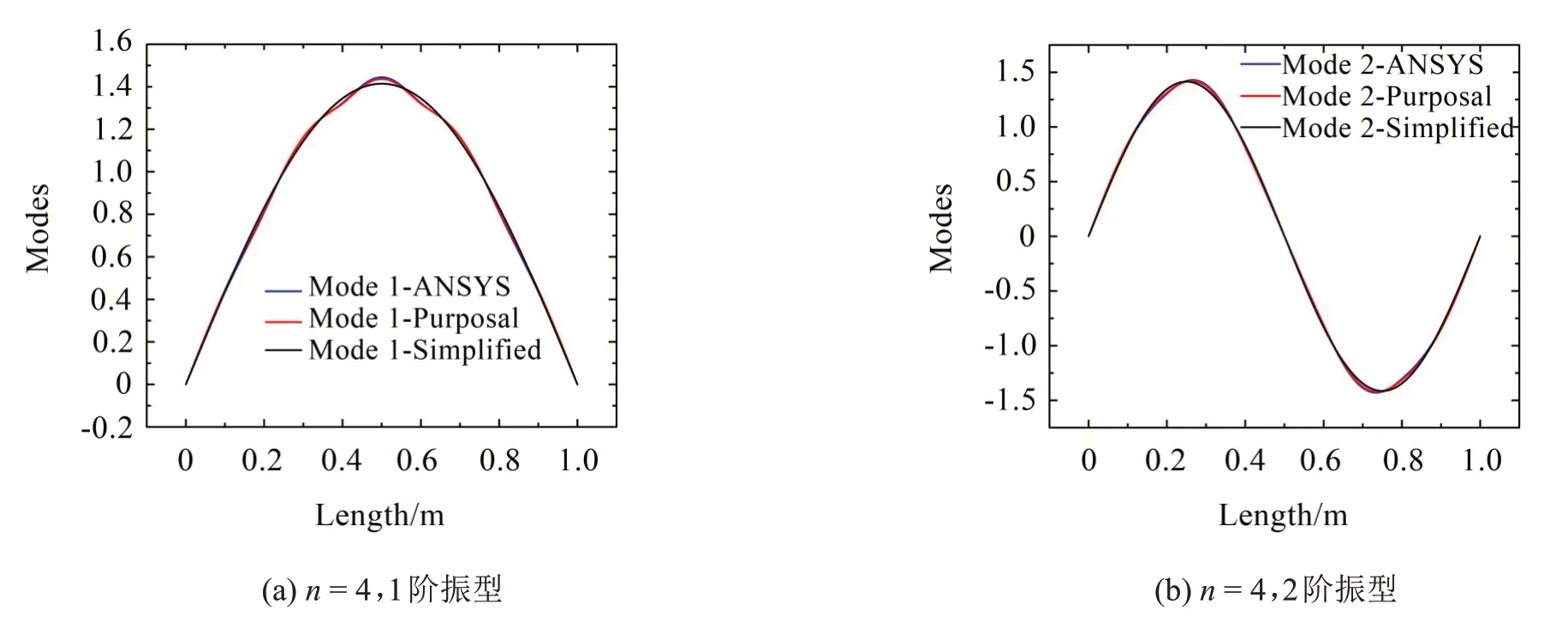
图7 n=4时周期性离散支承梁的前2阶振型（算例3）

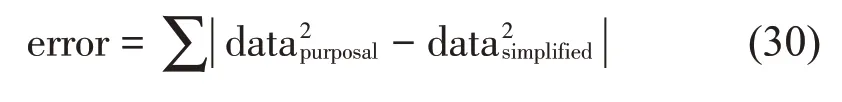
3 结语

本文针对离散支承梁建模过程中使用对应简支梁简化振型方法的适用范围进行了分析与讨论。

(1)相比于通过狄拉克函数直接将支承刚度以外力项纳入轨道动力学模型的做法[8]，本文提出了一种可以得到解析振型函数的分段动力学建模方法，以n个离散支承为节点，把简支梁划分为n+1段，且单独考虑了支承处对应短梁的长度ΔL，与现实情况下的离散支承梁结构更为贴近。

(2)通过对比动力学建模与有限元仿真结果，验证了本文所提出的分段建模方法的准确性和可靠性。针对周期性较差、计算长度不足或出现某一节周期性缺失的情况，采用本文提出的方法依然能够准确求得梁的各阶振型和固有频率，可为之后强迫振动响应的求解奠定理论基础。

(3)讨论了支承刚度对离散支承梁固有频率的影响。当支承刚度增加时，包含n个离散支承的简支梁的前n阶固有频率会逐渐增大并收敛于第n+1阶固有频率，直至弹性支承可被近似视作固定约束。

(4)讨论了简化简支梁振型的误差随计算长度的变化关系。对比3 种方法求得的振型函数发现，对标有限元分析结果修正振型能够准确表征离散支承特性，且随着计算长度的增加，简化简支梁振型与修正振型之间的误差逐渐显小，最终收敛于一非零定值。