Dynamical analysis,circuit realization,and application in pseudorandom number generators of a fractional-order laser chaotic system∗
Chenguang Ma(马晨光) Santo Banerjee Li Xiong(熊丽) Tianming Liu(刘天明)Xintong Han(韩昕彤) and Jun Mou(牟俊)
1School of Information Science and Engineering,Dalian Polytechnic University,Dalian 116034,China
2School of Physics and Electromechanical Engineering,Hexi University,Zhangye 734000,China
3Department of Mathematical Sciences,Giuseppe Luigi Lagrange,Politecnico di Torino,Corso Duca degli Abruzzi 24,Torino,Italy
Keywords: fractional-order laser chaotic system,SE complexity,intermittent chaos,NIST test,circuit realization
1. Introduction
Advantages of chaotic systems such as the extreme sensitivity to initial values, the inherent randomness, ergodicity make them prime candidates for scrambling and diffusion in image encryption process.[1–12]However, with development of technologies such as deep learning and artificial intelligence algorithms, predicting low-dimensional simple chaotic sequences has become a piece of cake.[13,14]This situation will lead some secret communication schemes based on this chaotic sequence fragile and easy to crack. Therefore, constructions of chaotic systems with high dimensionality and complex dynamical behaviors are favored by scholars.[15–19]
Laser chaotic systems are widely used in the field of optical secure communication because they can quickly generate high-dimensional broadband, high-frequency, and strong nonlinear chaotic signals.[20–28]A surging number of scholars spare no effort to study laser chaotic systems. For instance, Kadhimet al.[29]constructed a new four-dimensional laser chaotic system by introducing complex variables into a Lorentz–Haken system, and designed a random sequence generator based on this system, Ranet al.[30]constructed a new master-slave laser chaotic system, analyzed its dynamical characteristics,and used this system to construct a random sequence generator. Reports on low-dimensional laser chaotic systems are not uncommon. However, there are few reports on the construction and realization of high-dimensional laser chaotic systems.
Fractional calculus is not a novel concept, its unique memory effect makes it more suitable for describing the process-related physical phenomena, but its development has stagnated due to computational difficulties. Fortunately,fractional calculus has been applied to various fields due to the increase in computing power, such as signal processing, image detection, control systems, and financial systems.[31–35]Integer calculus,as a special case of fractional calculus,hides many properties of physical phenomena. A growing number of academicians devoted themselves to discovering special properties of fractional-order systems.[36–38]By introducing fractional calculus to a chaotic system, the bifurcation parameters of the system can be expanded, and some complex behaviors such as state transitions and bursting oscillations will appear. Therefore, fractional-order chaotic systems(FOCSs)have attracted attention of scholars.[39–48]Heet al.[49]found through numerical simulation that time-varying order will change dynamical behaviors of an FOCS. Maet al.[50]analyzed multi-stable behaviors of an incommensurate FOCS, and also analyzed the influence of order of different sub-equations in the system equation on the bifurcation behavior of the system. Wanget al.[51]analyzed the complex dynamical behaviors of an FOCS with coexisting hidden attractors and designed a circuit to verify the characteristic of the FOCS.Research and implementation of FOCSs are still in infancy,requiring further investigations by scholars.
Based on the above discussion, strong curiosity drives us to explore dynamical characteristics of a high-dimensional fractional-order laser chaotic system(FOLCS).Therefore,we propose a new five-dimensional(5D)FOLCS,analyze the dynamical behaviors,realize it by a circuit and apply it to a pseudorandom number generator(PRNG).The rest of the paper is arranged as follows: The model of the FOLCS,its properties and numerical solution process are given in Section 2. Section 3 analyzes some dynamical behaviors of the FOLCS,including some special behaviors such as state transitions and coexistence of attractors. The circuit implementation of the system and its application in the PRNG are introduced in Sections 5 and 6,respectively.Finally,some conclusions are summarized in Section 7.
2. Model of the new laser system and the numerical solution of its fractional-order form
2.1. The model and its properties of the laser chaotic system
A new Lorentz–Haken-type laser system with the hostnonlinearity is expressed as

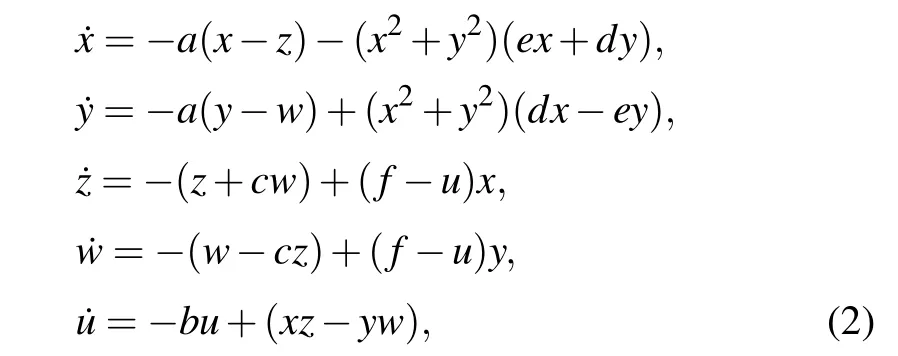
where(x,y,z,w,u|x,y,z,w,u ∈R)are state variables,anda,b,c,d,e,fare bifurcation parameters. Obviously,the system remains unchanged under coordinate transformation (x,y,z,w,u)→(−x,−y,−z,−w,u), that is, the system remains unchanged when rotated 180◦around theuaxis. The factors that affect the divergence of the system(2)read

It can be seen from Eq.(3)that the divergence of the laser system is not only related to parameters,but also affected by state variables. Introducing the Caputo differential definition in the laser chaotic system(2),the 5-D FOLCS can be expressed as
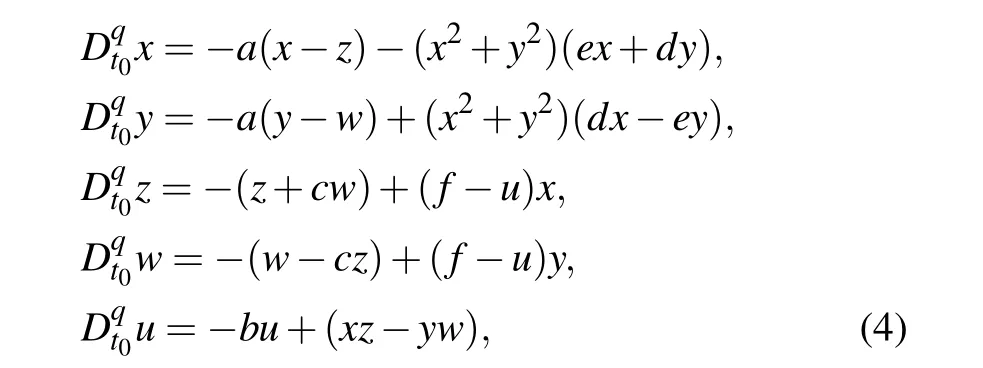
whereqis a non-integer derivative.
In order to explore stability of the equilibrium point of the FOCS, we investigate the stability of the equilibrium points of the real number field of the system (2). Let the left side of Eq. (2) be 0, the equilibrium point can be obtained asE0=(0,0,0,0,0), and substitutingE0into the Jacobian matrix of system(2),one can reach

For simplicity, leta= 8,b= 1,c=−0.36,d=−0.01,e= 0.005,f= 38, the characteristic values at the equilibrium pointE0are 13.2825±0.2154i;−22.2825±0.1446i;−1. Obviously,E0is an unstable saddle point under these conditions. For the FOCS,its equilibrium point will be stable if the eigenvalue of the Jacobian matrixJat the equilibrium point satisfies the following equation:

2.2. The numerical solution of the FOLCS
Based on the ADM algorithm, the numerical solution of the FOLCS can be expressed as
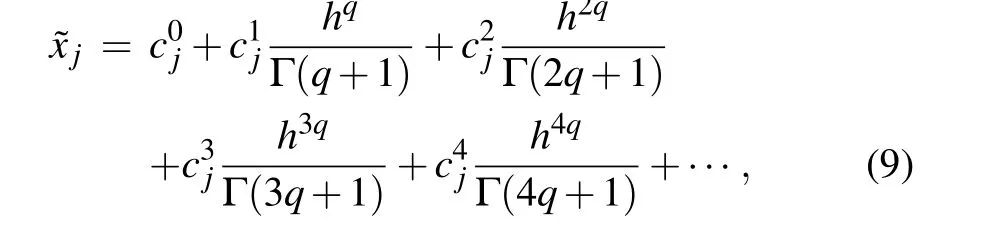
wherej= 1,2,3,4,5, and the step sizeh= 0.01 is always maintained in this study. In this paper,the first 5 items are intercepted,which can not only guarantee the calculation accuracy but also reduce the calculation time. Assuming the initial valuex0=[x01,x02,x03,x04,x05],and the related gamma functions are represented by Eq.(10),then the coefficientscijare shown as follows:
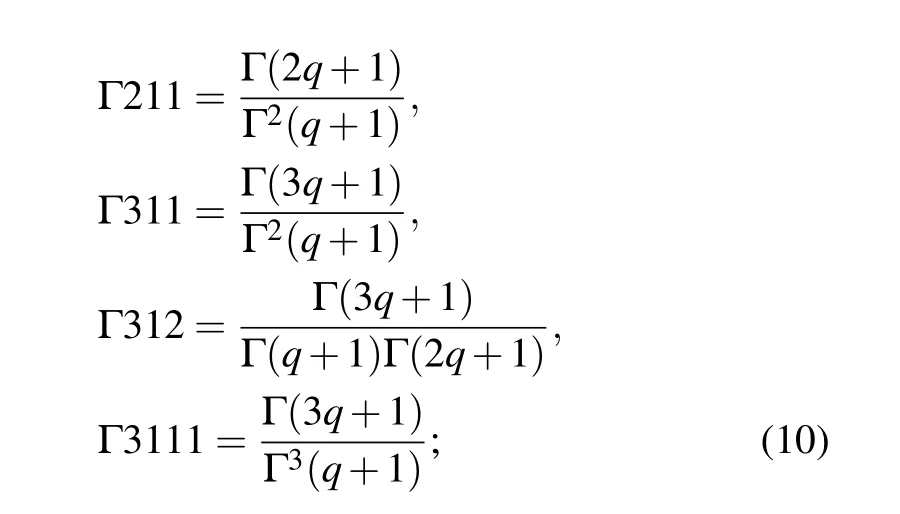

Whena=8,b=1,c=−3.8,d=−0.3275,e=0.003,f=38,q=0.9, the initial valuex0=[−3,1,5,10,−7], the attractor projections of the system are shown in Fig.1. Under these conditions,the Lyapunov exponent(LE)of the system are 0.9058,0,−7.9739,−34.8478,−38.2401,and the Lyapunov dimensionDL=2.1136.

Fig.1. The projections of attractor on(a)x–u plane,(b)z–u plane,and(c)w–u plane.
3. The dynamical behaviors of the FOLCS
3.1. Dynamical characteristics influenced by parameters and orders
It is a very effective method to explore the dynamical behaviors of the system at different orders through the bifurcation diagram and the Lyapunov exponent spectrum. Figure 2 shows the detailed bifurcation behaviors and Lyapunov exponent (LE) values of the system with the orderqwhena=8,b=1,c=2.1,d=0.01,e=0.02,f=38, with the initial valuex0=[1,1,1,1,1]. The first three LEs’ curves are provided here to clearly capture the changes in the system state.The data shows that whenq=0.652,the maximum LE(MLE)of the system is 4.018. It can be seen from Fig. 2 that the larger the orders,the smaller the LE values,which means that the randomness of the sequence generated by the integer-order system is worse than that of the fractional order.
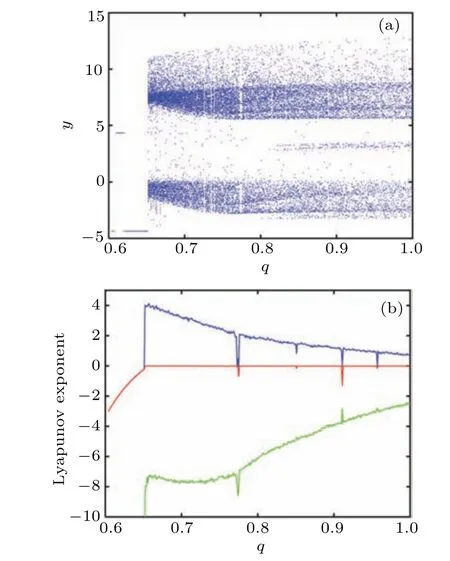
Fig.2. Dynamical behaviors versus q: (a)bifurcation diagram,(b)Lyapunov exponent.
A conspicuous advantage of this FOLCS is that it has multiple bifurcation parameters and there are multiple paths to chaos. Taking the variable parametercas a case, whena=8,b=1,d=0.01,e=0.02,f=38,q=0.9 and under the initial conditionx0=[1,1,1,1,1],the bifurcation diagram and LEs varying with parametercare shown in Fig. 3.It can be seen from Fig.3(a)that as the parametercincreases,the system enters a chaotic state from period-doubling bifurcation. Interestingly, the period-doubling bifurcation, boundary crises points and reverse period-doubling bifurcation can be seen clearly in the partially enlarged diagram in Fig. 4, and the data record thatc=−3.901,3.797 are the boundary crises points. The MLE=2.151 is located atc=3.96. The results of the MLE and SE complexity of the system varying with the parametercwith different orders are shown in Figs.5(a) and 5(b). Overall, the smaller the order, the larger the MLE and the higher the SE complexity of the system. However, as the order decreases,more periodic windows appear in the system.Whenq=0.9,the system has not only a larger chaotic range,but also a larger MLE.
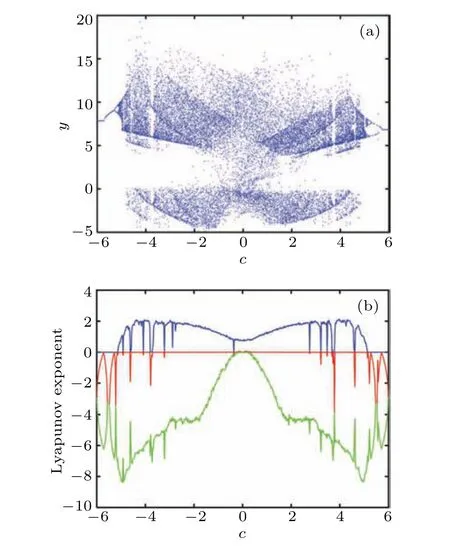
Fig.3. Dynamical behaviors versus c: (a)bifurcation diagram,(b)LEs.

Fig.4. Partial enlarged view of bifurcation:(a)and(b)partial enlarged view of period-doubling bifurcation,(c)partial enlarged view of reverse period-doubling bifurcation.

Fig.5. The system performance versus c: (a)the MLE,(b)the SE complexity.
The changes of other bifurcation parameters and the corresponding first three LEs are shown in Fig.6.

Fig.6. The impact of parameters on system status with(a)parameter a,(b)parameter b,(c)parameter d,(d)parameter e,(e)parameter f.
3.2. Coexistence of attractors
Under three different initial conditions,the chaotic attractors coexist with two different sinks whena=10,b=0.9,c=0.8,d=−0.01,e=0.088,f=29,q=0.9,as shown in Fig.7. In Fig.7,the trajectories,with initial values of

are represent by red, blue and green, respectively. It can be seen from the time domain diagram that both red and blue trajectories degenerate from the chaotic state to a sink,but the degeneration time and the final state position are different. However, the green trajectory always maintains the chaotic state.In addition,the MLEx2>0 all the times,but the MLEx0<0 aftert=8675 s and the MLEx1<0 aftert=3050 s. The above discussion shows that small differences in initial values will lead to different final states of the system.
Figure 8 shows that the system has two coexisting weak chaotic attractors. Under the conditionsa= 8,b= 1,c=−1.68,d=−0.01,e=−0.005,f=38,q=0.7, red is for the initial valuex0=[10,0,3,1,−2], and blue is for the initial valuex1=[3.26,−3.58,3.6,−4.8,36.16]. From the timedomain waveform and the evolution of LE over time,it can be seen that both the relatively weak chaotic attractors are transferred from the same strong chaotic attractor. However, the conversion times are different.

Fig.8. Coexistence of two chaotic attractors: (a)strong chaotic state, (b)two different weakly chaotic state, (c) the y waveform with different initial values,(d)the first two LEs changing with time under different initial values.
The other types of coexisting attractors are shown in Fig.9,and its corresponding parameters and the initial conditions are listed in Table 1.
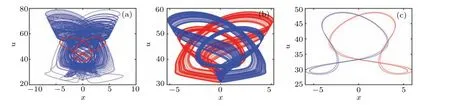
Fig.9. Other types of coexisting attractors. (a)period-chaotic;(b)chaotic-chaotic;(c)period-period.

Table 1. The parameters,initial values,colors and coexisting type corresponding to Fig.9.
3.3. State transition and intermittent oscillation(breather)
Whena=8,b=1,c=−0.36,d=−0.01,e=−0.003,f=38,q=0.9, the state of the system will shift with time,as shown in Fig. 10. Under these sets of parameters, the final periodic attractor is degenerated from the chaotic attractor, but the degradation time is 800 s for the initial valuex0=[3.26,−3.58,3.6,−4.8,36.19], and 5100 s for the initial valuex1=[1,1,1,1,1].Correspondingly,we have the MLEx0,x1=0 after 800 s and 5100 s,respectively.
Whena=8,b=1,c=3.797,d=−0.01,e=−0.005,f=38,q=0.9,the time-domain waveform,LEs,and attractor that change with time are shown in Fig. 11. One can see from the time-domain waveform that the periodic oscillation of system state variables will be interrupted by random finite burst oscillations,and when the burst oscillation ends,the periodic oscillation will restart again.The trend of LEs changing with time can also prove that the system alternates between short-term chaos and periodic oscillation.
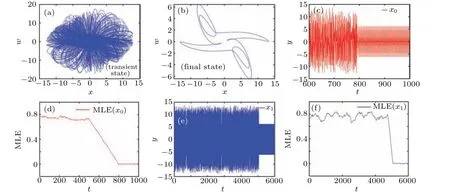
Fig.10. Chaotic states degenerates to periodic state: (a)transient state,(b)final state,(c)the waveform of the y with x0,(d)the MLE with x0,(e)the waveform of the y with x1,(f)the MLE with x1.
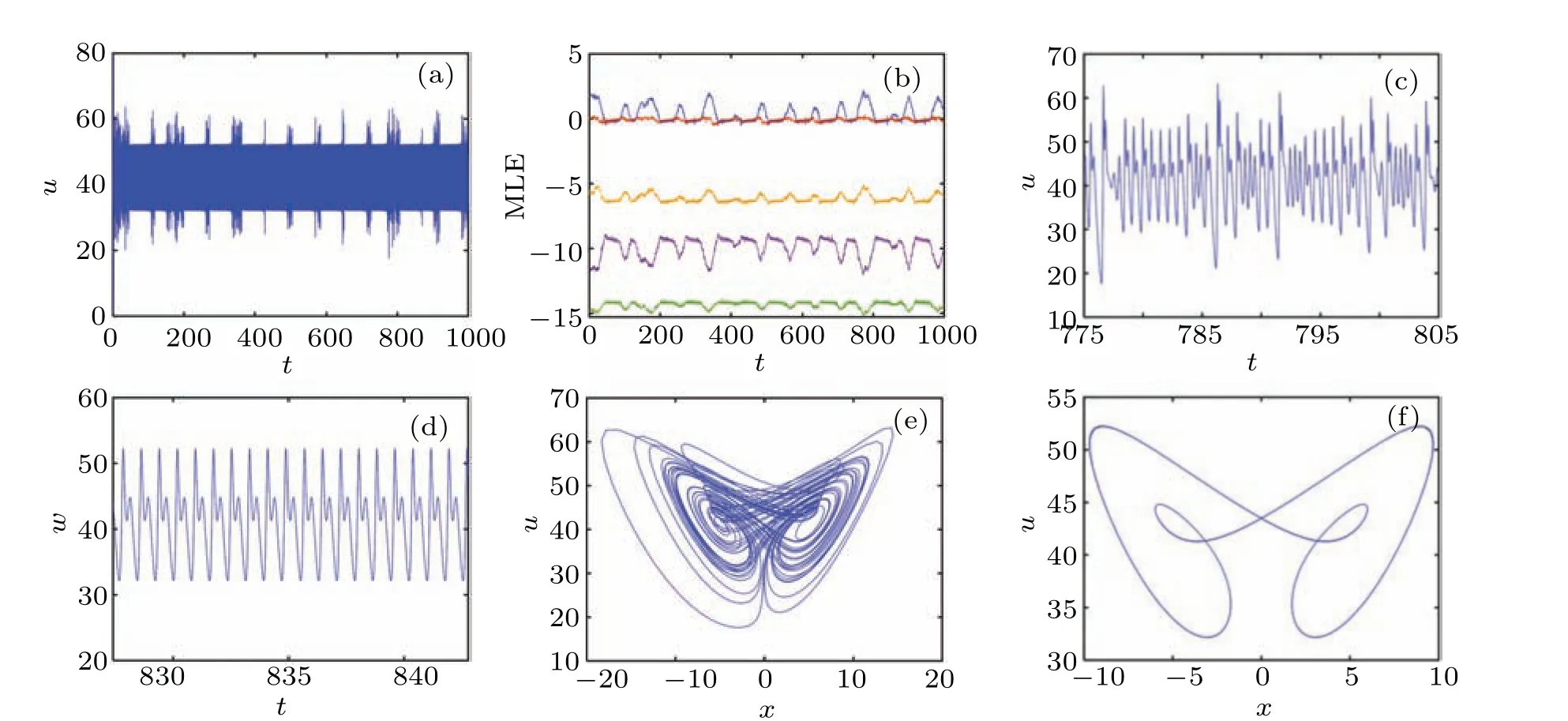
Fig. 11. Intermittent oscillation between the burst and periodic: (a) time-domain waveform, (b) the LEs changing with time, (c) the burst oscillation,(d)the periodic oscillation,(e)the burst oscillation attractor,(f)the periodic oscillation attractor.
3.4. Attraction basin and complexity analyzes
Using the attraction basin can easily find the parameters space of the system in a chaotic state, which is very effective in secure communication based on chaotic systems. Figure 12 detects the state distribution of the laser system on different parameter planes. In the figure,black represents the divergent state, red means stable point, yellow indicates periodic and blue means chaos.This means that the parameters corresponding to the blue area should be selected in chaotic cryptography.
In order to further find out the chaotic regions with high complexity, the spectral entropy complexity algorithm which can reflect the energy distribution of any signal in the frequency domain is considered here to measure the structural complexity of the FOCS,as shown in Fig.13. The more balanced the energy distribution,the higher the complexity of the sequence structure,so the larger the SE value. The color levels are mapped to the level of system complexity. The initial value is setting asx0=[1,1,1,1,1]and the parameters’conditions,maximum SE values and the corresponding coordinates are given in Table 2. One can see from a longitudinal point of view of Fig. 13(a) that, asqdecreases, the complexity of the system becomes larger. However,whenqis less than a certain value,the complexity of the system becomes smaller,and the system even diverges (white area). The maximum SE under this condition is 0.7703 witha=8.4,q=0.65. A larger SE value indicates that the fractional-order system can generate chaotic sequences with higher complexity.
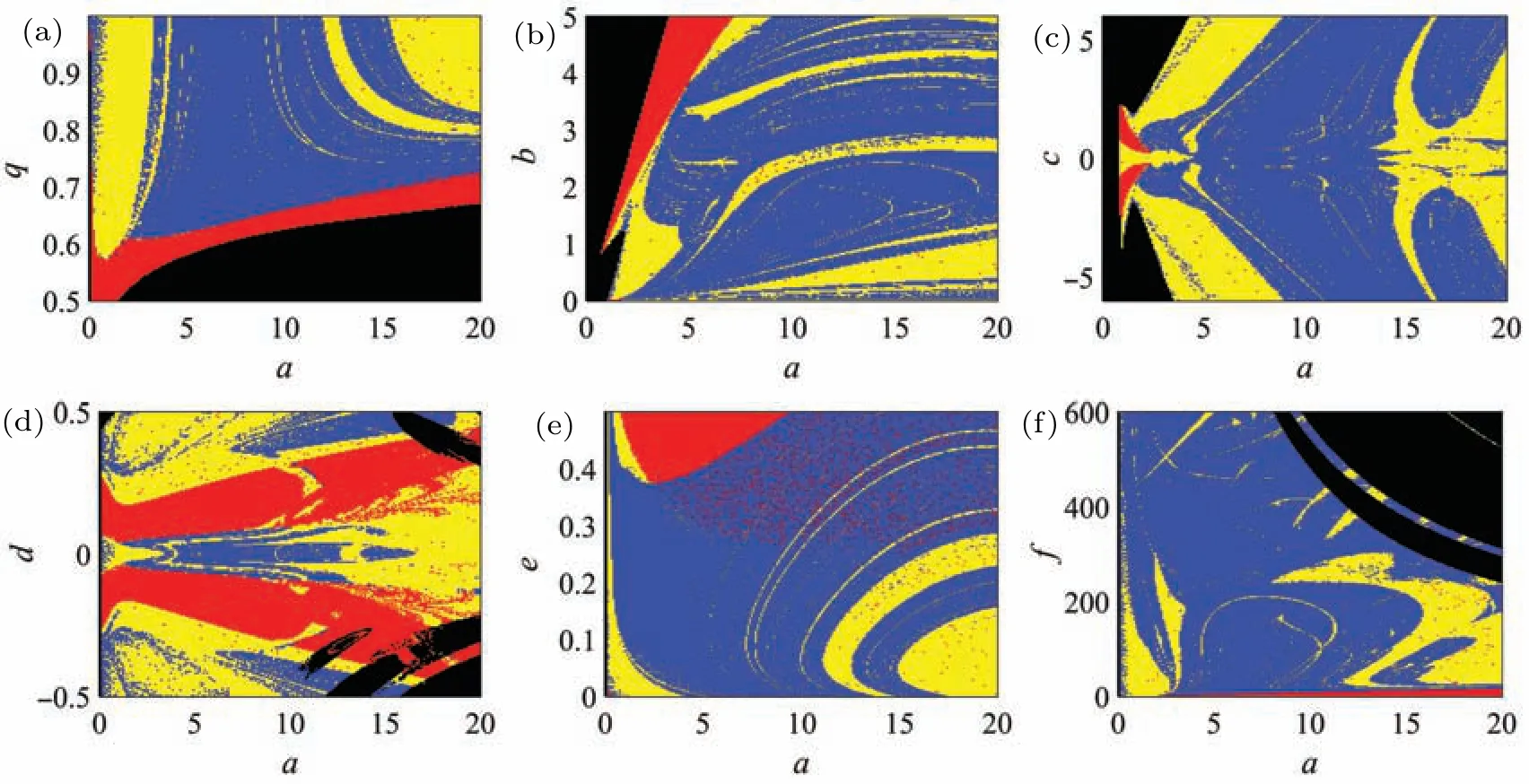
Fig.12. The attraction basin with different parameters’planes: (a)a–q plane,(b)a–b plane,(c)a–c plane,(d)a–d plane,(e)a–e plane,(f)a–f plane.
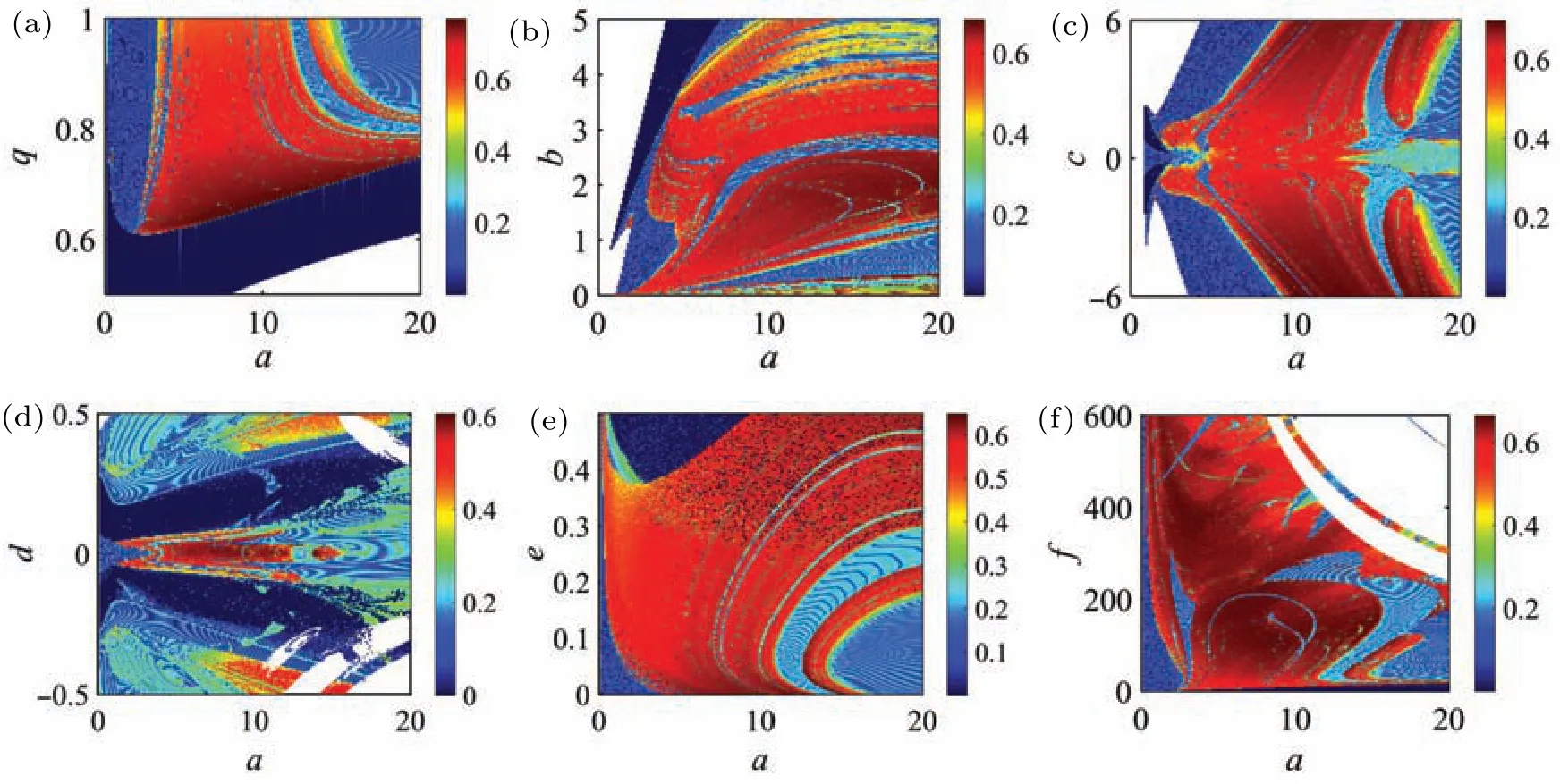
Fig.13. SE complexity diagram of different parameters planes: (a)a–q plane,(b)a–b plane,(c)a–c plane,(d)a–d plane,(e)a–e plane,(f)a–f plane.
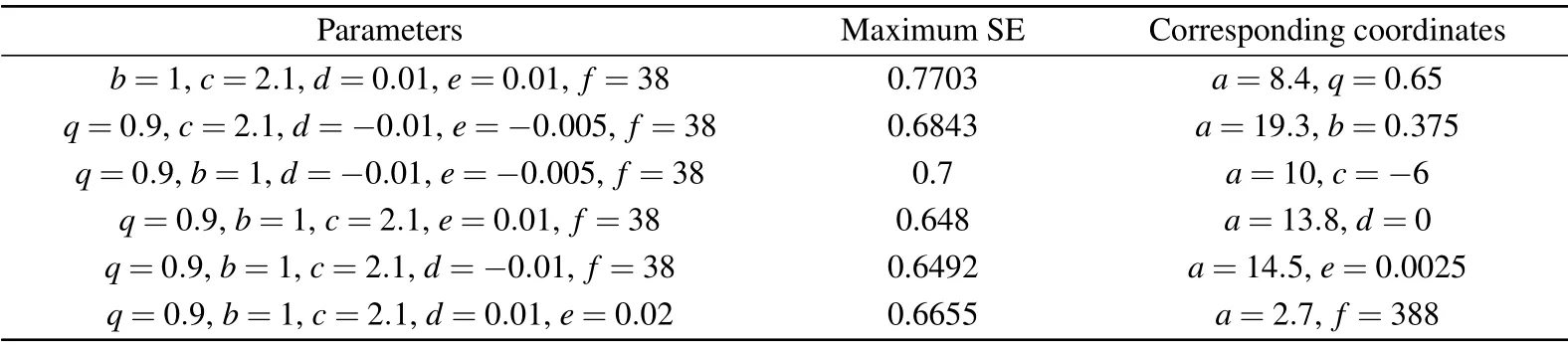
Table 2. Parameters of the SE complexity diagram(Fig.13).
4. The circuit realization of the FOLCS
Here,TMS320F28335 is used as the core processor to realize the 5-D FOLCS.The experimental system can be seen in Fig.14.
Set the same parameters and initial value as in Fig.1,and the DSP output sequence randomly intercepted on the oscilloscope is shown in Fig.15.

Fig.14. The circuit test bench.

Fig.15. The output sequences by DSP:(a)x–u sequence,(b)z–u sequence,(c)w–u sequence.
Compared Fig.15 with Fig.1,it can be seen that the DSP simulation results match well with the computer simulations.This indicates that the chaotic oscillation of the system can be realized on the DSP platform,which provides a guarantee for the application of the FOLCS.
5. PRNG based on the FOLCS
Pseudo-random numbers based on chaotic sequences play a vital role in image encryption, information hiding, digital authentication and other cryptographic fields. The seed of the PRNG can be the initial value and bifurcation parameters of the chaotic system. The output chaotic sequencexican be represented by a certain number of binary numbers,but there may be correlation between these numbers. Therefore, some of them can be selected to generated random sequence to reduce the correlation. Combining the parameters range given by the attractor basin and SE complexity chaotic diagram analyzed in Subsection 3.4,the chaotic region with high complexity should be selected as the seed of the PRNG.It is important to note that the divergence state of the black region,the stable point of the red area and the period state of the yellow area cannot be used as the seed of the PRNG. Algorithm 1 is the generation algorithm of this chaos-based pseudo-random sequence generator.

Algorithm 1. The the PRNG based on the FOLCS Input: the parameters of the system.(2)For i=1 to 5 do Get data Pi: intercept a section of the chaotic sequence xi;Transform Pi to 32-bit binary;Extract the last 8 bits of the 32-bit binary;end for Output: Five the PRNG based on xi.

Table 3. The NIST test results.
There are many existing detection methods for random sequences, among which NIST test is the most widely used statistical detection method. The NIST-800-22 kit will evaluate the sequence from 16 different aspects and obtain apvalue. It is generally believed that when the obtainedpvalue is greater than 0.01, it is a random sequence with 99%confidence. Set the initial valuex0=[−3,1,5,10,−7],parameters(a,b,c,d,e,f,q)=(8,1,−3.8,−0.3275,0.003,38,0.9) are selected as the seed of the PRNG. Five PRNGs will be obtained according Algorithm 1, and each the PRNG contains 1000000 binary bits.The test results of NIST-800-22 are listed in Table 3.
6. Conclusion
By introducing the Caputo differential operator, this paper constructs a new 5-D FOLCS.The dynamical characteristics of this system are analyzed by numerical solution. Compared to the corresponding integer-order system, the dynamical characteristics of the system in the fractional-order form are more complex,which is reflected in the fact that the maximum LE value of the system decreases with the increase of the order. The simulation results show that when the orderq=0.9, as the parametercchanges, the system not only has a larger LE value and SE complexity, but also has a larger parameter space making the system in a chaotic state. In addition, the laser system exhibits rich multi-stable behaviors, including the coexistence of chaotic attractors and two sinks,the coexistence of two symmetric chaotic attractors,and the coexistence of chaotic attractors and limit cycles.Meanwhile,there are two types of oscillation transitions in this system. One is that chaotic oscillations degenerate into periodic oscillations.The other is the endless alternate appearance of chaotic oscillation and periodic oscillation. The parameters corresponding to the high-complexity sequence that the system can generate are found through the SE complexity diagram. For example,when fixedb=1,c=2.1,d=0.01,e=0.01,f=38, the maximum SE=0.7703 whena=8.4,q=0.65. In addition,the simulation results of the digital circuit proposed in this article are consistent with the computer numerical simulation results,that is,the chaotic oscillation of the system is verified on the circuit.Finally,the PRNG based on the FOLCS has passed the NIST-800-22 test. In short, the theoretical and numerical simulation have proved that the FOLCS has rich chaotic characteristics. In the future, we will explore applications of this system in the field of image encryption.
- Chinese Physics B的其它文章
- Transient transition behaviors of fractional-order simplest chaotic circuit with bi-stable locally-active memristor and its ARM-based implementation
- Modeling and dynamics of double Hindmarsh–Rose neuron with memristor-based magnetic coupling and time delay∗
- Cascade discrete memristive maps for enhancing chaos∗
- A review on the design of ternary logic circuits∗
- Extended phase diagram of La1−xCaxMnO3 by interfacial engineering∗
- A double quantum dot defined by top gates in a single crystalline InSb nanosheet∗

