与月球有关的引潮力

金咸宜

(原上海船舶工业公司所属新中动力机厂培训中心，上海 200083)

潮汐是地球表面壮观的自然现象．潮汐现象的主要特征是，海洋在随地球自转的过程中，到达近月点时涨潮，然后退潮，到达远月点时又涨潮，然后又退潮，每日两次涨落．近月点的潮位比远月点稍大．地表海水，相对于地球自转轴，呈不对称的纺锤体形(见图1示意)．

图1 海洋在近月点和远月点涨潮

潮汐是由于地球附近天体如月球和太阳，对地表物体(主要指海水)存在作用所造成的．月球离地球最近，作用也最大．已有各种方法，运用力学原理，引入引潮力的概念，以解释月球对潮汐现象的主要作用．

本文试图以另一种角度，即从简化的地月二体系统的力学模型入手，比较严格地推导出与月球有关的地表物体动力学方程，转换到固连于地月系统的转动坐标系中，使用对称性原理对方程各项进行分析，排除与潮汐无直接关联的项，从而确定引潮力．

1 简化的地月系统力学模型

建立一个简化的地月二体系统的力学模型．在惯性参考系中，地球质量为m地，质心在O1点，月球质量为m月，质心在O2点．O1和O2两点之间的距离为常量L(此处忽略了地月之间距离的变化)．在一个固定的平面内，地月二体绕系统的质心O点作匀速转动(此处忽略了地月绕太阳和银河系中心等的复杂运动)，转动角速度ω沿该平面的法线方向．O和O1两点之间的距离为常量a．

建立一个惯性坐标系(见图2)．原点在O点．z轴与角速度ω重合．Oxy平面即系统的转动平面．x轴可以这样设定：在某一初始时刻，当O1和O2两点之间的连线正指向天空中某一恒星时，设x轴从O点指向该恒星．

再建立一个转动坐标系．坐标系的原点、z轴和Oxy平面的设定，与上述惯性坐标系相同．而x轴，则固定在O1和O2两点的连线上．可见此坐标系在初始时刻与惯性坐标系完全重合(见图2)，然后以角速度ω相对惯性坐标系作匀速转动，是一个非惯性的坐标系．

最后，在力学模型中加入地球的自转．设地球相对于以上建立的转动坐标系，绕通过地球南北极的自转轴，以角速度ω1匀速转动，ω1与ω平行，因而也与z轴平行(此处忽略了ω1和ω之间的夹角)．因而在惯性坐标系中，地球绕地球自转轴，是以角速度ω+ω1作匀速转动的．

本文后续的讨论就以此力学模型为基础，在惯性坐标系和固连于地月系统的转动坐标系中分别进行．

2 地表物体的运动参量

如有物体(如海水)质量为m物，位于地表任意一点P．设此物体相对地球静止，只随地球的运动在惯性坐标系中运动．分析该物体的各运动参量．

(1)

此径矢是时间t的函数．其中a以角速度ω绕z轴转动．R既以角速度ω绕z轴转动，同时又以角速度ω1绕地球自转轴转动．

物体的速度如下式所示，其中利用ω和ω1方向相同的性质，可得

(2)

把速度对时间微分，得到物体的加速度，并利用ω和ω1方向相同，以及ω和ω1为匀速转动的角速度，因而对时间的微分为0的性质，可得

ω×(ω×a)+(ω+ω1)×((ω+ω1)×R)

(3)

并得物体质量与加速度的乘积为

(4)

3 惯性坐标系中的动力学方程

由质量与加速度的乘积，即可得到惯性坐标系中地表物体的动力学方程：

m物ω×(ω×a)+m物(ω+ω1)×[(ω+ω1)×R]

(5)

其中力F由3项组成，代入得

m物ω×(ω×a)+m物(ω+ω1)×[(ω+ω1)×R]

(6)

等式右边第1、2项，是物体质量与加速度的乘积．由于ω和ω1方向相同，第2项可拆分为三项之和：

m物(ω+ω1)×[(ω+ω1)×R]=

m物ω×(ω×R)+2m物ω×(ω1×R)+m物ω1×(ω1×R)

(7)

因而方程可写为

m物ω×(ω×a)+m物ω×(ω×R)+

2m物ω×(ω1×R)+m物ω1×(ω1×R)

(8)

4 转换到固连于地月系统的转动坐标系

把动力学方程从惯性坐标系转换到非惯性的转动坐标系，只要在等式右边，只保留物体质量与在转动坐标系中的加速度的乘积，而把其余各项变号后移到等式左边，有

m物ω×(ω×a)-m物ω×(ω×R)-

2m物ω×(ω1×R)=m物ω1×(ω1×R)

(9)

对等式左边各项说明如下：

第1至第3项同上，不再重复．第4、5项之和利用式(1)可写为

-m物ω×(ω×a)-m物ω×(ω×R)=

-m物ω×[ω×(a+R)]=

(10)

可见这是物体在转动坐标系中所受的惯性离心力．第6项则是物体在转动坐标系中所受的科里奥利力．只要代入物体相对于转动坐标系的速度

ω1×R=V

(11)

可得

-2m物ω×(ω1×R)=-2m物ω×V

(12)

这正是科里奥利力．

5 按对称性原理确定引潮力

对上述动力学方程等式左边的6项进行分析，判断是否是形成潮汐的原因，把无直接关联的项排除掉，留下的项就是引潮力．这个判断可以用对称性原理来实现．按对称性原理，结果中的不对称性必在原因中有所反映，即原因中的不对称性至少有结果中的不对称性那么多[1]．如前所述，潮汐现象相对地球自转轴具有显著的不对称性，这种不对称性必在其原因即引潮力中有所反映．引潮力至少要有同等的不对称性．在这6项中，凡是相对地球自转轴对称的项，不可能是形成潮汐的原因．只有相对地球自转轴不对称的项，才可能成为引潮力．

第1项相对地球自转轴显然是对称的．第3项是一个非主动的力，不在考虑之列．第5项，由于R是由地球质心O1指向地表某点P的矢量，二次矢乘的结果，是由地球自转轴垂直向外发散的矢量，其方向和大小在地表各点的分布，相对地球自转轴具有对称性．第6项，如考虑ω和ω1的方向是相同的，那么分析的方法和结果就与第5项相同．由此可见，第1、3、5、6项都应该被排除在引潮力之外．

再分析剩下的第2、4项．为表达方便，用j表示第2项，有

(13)

这一项是月球引力．由于其相对月球质心O2是球对称的，因而，相对地球自转轴没有对称性．用k表示第4项，有

k=-m物ω×(ω×a)

(14)

这一项已知是物体在转动坐标系中所受惯性离心力的一部分．从公式可见，这是一个常矢量，在地表任一点上，方向都与x轴平行且反向，大小则等于常量m物ω2a，因而此项也是相对地球自转轴不对称的．把第2、4项相加，就得到了引潮力，用F引潮表示，有

(15)

6 若干说明

通过上述方法分析所得的引潮力，与通过其他方法得到的结果完全相同[1]．

对所得引潮力公式进行简单的计算，可以看到与地球潮汐现象的实际也相符合．

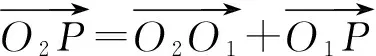
r=L+R

(16)

把此式和

r2=L2+R2-2RLcosφ

(17)

以及

k=-m物ω×(ω×a)=m物ω2a

(18)

代入式(15)，可得

(19)

由此式，不难在Oxy平面中以直角坐标分量的形式求得地球赤道上任一点处物体所受的引潮力．若再考虑式(15)和式(19)对x轴的对称性，实际上已可求得地表任何一点处的引潮力．

现把在Oxy平面和Oxz平面上若干点处单位质量物体所受引潮力的计算结果，标示在示意图中(见图3)． 从图中可以看到，在近月点和远月点，引潮力数值最大，方向都指向当地上空，对海水起到提升的作用．近月点的引潮力比远月点稍大．在近月点与远月点的中间点，引潮力数值最小，且方向都指向地心．其余地点，数值和方向各有不同．将此图与图1所示的海洋涨潮和退潮的示意图对照，可以看到明显的正相关性．

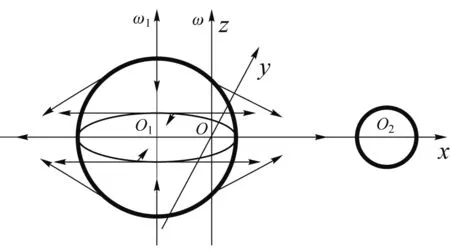
图3 地表各点物体所受引潮力示意图

最后必须说明的是，在本文第2节中，使用了地表物体在某点相对地球静止的简化条件．而通常在实际情况下，海水常常是流动着经过该点的．自然，海水在流经该点时，也会受到与静止时相同的引潮力．但是，这里使用的简化条件，以及把引潮力的计算结果与潮位的大小对照的方法，毕竟是一种准静态和定性的解释．更准确的定量分析，则应该从流体静力学的观点，去近似求得在引潮力作用下的海平面几何形状的变化[2]．也可以在一定的简化条件下，求得地球周围海水圈在各种外力包括引潮力作用下的流体力学方程的全积分．从而掌握地表海洋随地球自转而与时间有关的全部动态过程．进而了解海水如何提升，洋流如何在地球各处涌动，以及潮汐如何相对近月点和远月点的位置发生迟延等等．但这显然已超出了本文的讨论范围．

本文仅限于从推导与月球有关的地表物体动力学方程着手，在非惯性的转动坐标系中，用对称性的讨论来确定和计算引潮力，从而提供一种可取的分析方法，有助于加深对引潮力和地球潮汐成因的理解，作为一个运用力学原理来提高解题能力的实例，为进一步的分析和研究打下基础．

致谢：感谢于凤军教授的热情指导．