盖尔圆的性质及其应用 ①

张仙凤

(朔州师范高等专科学校 数计系，山西 朔州 036002)

0 引 言

力学、工程学中特别多的难题，都与数学中的特征值问题紧密相连。矩阵特征值问题在数学学科及相关科学技术领域都有广泛的应用。1931年Gerschgorin提出了著名的盖尔圆定理，使得高阶矩阵特征值估计变得可能。特征值估计是许多领域的特点，在诸多领域起着非常重要的作用。雍龙泉提出线性代数中增加盖尔圆定理的思考。本文中，盖尔圆相关定理与特征值的相似不变性巧妙结合，将矩阵中的盖尔圆放大或缩小，使得矩阵的盖尔圆盘变成独立的圆，使得对特征值估计进一步精确。同时对矩阵是否可对角化问题、矩阵的正定问题及是否为奇异矩阵的问题，做出判断。

1 基本概念

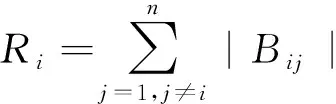
定理2：由矩阵B的所有盖尔圆组成的连通部分中，连通的盖尔圆个数等于B的特征值个数。(盖尔圆相重时按重复计数)。两个(或两个以上)盖尔圆中，任两点都可以用该范围内的一条折线连接起来，则这两个(或两个以上)盖尔圆就是一个连通的部分[1]。

2 基本性质

性质1：矩阵B有n个不同为特征值λi(i=12,…,n)，则B可对角化[2]。

性质2：相似矩阵有相同特征值[2]。

性质3:设B=(bij)∈Cn×n,若对所有i≠j,则|bii||bjj|>Ri(B)Rj(B)⟺detB≠0[3].

性质4：B=(bij)∈Cn×n，D=(dij)∈Rn×n，若dij≥|bij|(i=1,2,…,n)，则对B的任一特征值必有i，使得[ρ(D)表示D的谱半径]，dij≥|bij|⟹|λ-bii|≤ρ(D)-dii[3]

性质5：如果利用相似变换，矩阵D某盖尔圆被变大，则其它盖尔圆将会变小或不变；反之，则除它以外的盖尔圆会被放大或不变。

证明：由性质2，可构造对角F=diag(ε1,ε2,…,εn)

若εi>0(i=1,2,…,n).将矩阵B=(bij)∈Cn×n可写成如下形式：

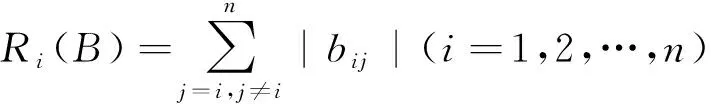
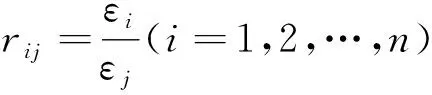
上市公司内部没有科学、系统的监督管理系统。监督机构没有履行自己的审查与监督责任，导致信息披露工作无法开展，效果不佳，直接影响了信息披露与审计工作效果。

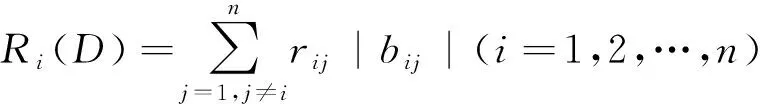
3 盖尔圆盘应用

3.1 对角化判别

阶数不高的矩阵对角化问题比较容易，但对于n阶甚至有未知文字的矩阵，此时对于特征值、特征向量的判断难度很大。

例1：证明矩阵B能够对角化，

分析：该矩阵为n阶方阵，对于求特征值、特征向量难度较大，假如令n=10n或30，利用计算机应用软件，可求得相应矩阵的特征值分布图，显然是实数，且互不相同，但怎样证明？

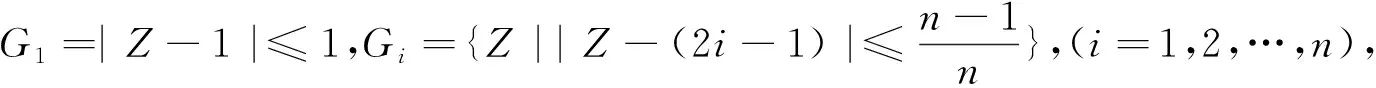
3.2 特征值估计

对于阶数比较大的矩阵(例如256×256的图像)，若det(E-B)=0是非常繁琐的。对于生活实际及工程、力学中的高阶矩阵，对于耗时耗力的求精确的特征值真的没有必要。可以对高阶矩阵的特征值进行估计，当其盖尔圆范围足够小，则估值就足够精准。这一过程对于所依赖的盖尔圆，只要其分离的合适，各个盖尔圆彼此独立，每个盖尔圆恰好含有一个特征值，这样特征值的范围就比较精准。

放缩盖尔圆的对角阵如何取？常常用如下关系：D=FBF-1对角矩阵D的选取，常用如下准则：变大第i个盖尔圆，则取di>1，其余dj=1(i≠j)；变小第i个盖尔圆，则取di<1，其余dj=1(i≠j).用来放缩的di≠1，直接作用于B的第i行的非主对角元素，当放缩第i个盖尔圆，同时也会不同程度放缩其它盖尔圆。

例2：估计矩阵

解：B的4个盖尔圆为：|Z-1|≤0.1+0.2+0.3=0.6；|Z-3|≤0.5+0.1+0.2=0.8；|Z+1|≤1+0.3+0.5=1.8；|Z+4|≤0.2+0.3+0.1=0.6,B的特征值全部都在如下这四个盖尔圆内，画在复平面上的图：孤立的盖尔圆G2和G4各是一个连通部分，对于盖尔圆G1和G3是一个连通的关系，该例子中共有三个连通部分。

图1 例2对应的盖尔圆

3.3 分离盖尔圆，将范围重叠的特征值隔离

例3：估计矩阵B的特征值，这里

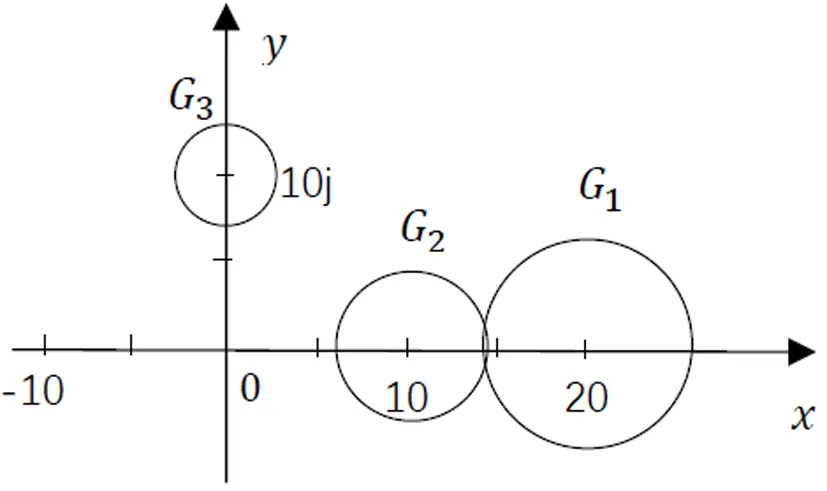
图2 例3对应的盖尔圆(分离前)

图3 例3对应的盖尔圆(分离后)

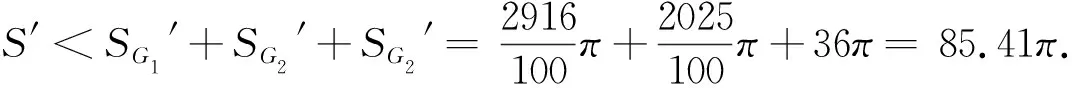
易见，这是3个孤立盖尔圆，B与D的特征值相同，且特征值在这三个盖尔圆中，注G3′中特征值就是G3中特征值，所以B的3个特征值分别位于G1′,G2′,G3′之中。通过盖尔圆理论来划分特征值区域，隔离特征值，将特征值隔离到较小范围内，提高估计特征值的准确率。

3.4 正定判定

设B是n阶实对称矩阵，在理论上，当实数t足够大，tE+B就正定。

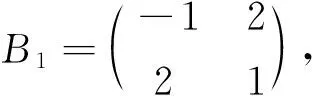
3.5 利用盖尔圆性质判别矩阵奇异性

解：R1(B)=2.1,R2(B)=2.8，R3(B)=2.6，|a11||a22|=6>2.1×2.8=R1(B)·R2(B)；；|a11||a33|=6>2.1×2.6=R1(B)·R3(B);|a22||a33|=9>2.8×2.6=R2(B)·R3(B)

根据性质3，可得detB≠0，即B为非退化矩阵。

本文利用盖尔圆相关性质，对不易求特征值的矩阵，利用矩阵某盖尔圆被放大，其它盖尔圆被缩小或不变；矩阵某盖尔圆被缩小，其它盖尔圆被放大或不变的性质，估计特征值的范围。在一定程度上，也可以估计非齐次特征值的范围。利用盖尔圆还可以处理矩阵对角化问题，还可以分析矩阵正定时参数的取值范围。盖尔圆的相关理论在矩阵扰动分析及优化理[4-5]中有重要的应用前景。