应用“等时圆”规律巧解时间问题

■吕良英

“等时圆”是由意大利著名物理学家伽利略提出的应用数学知识解决物理问题的经典模型。同学们在遇到一些涉及质点运动时间的问题时,如果能够通过数理分析,构建出“等时圆”,那么就可以运用“等时圆”规律快速做出判断,省时又省力。下面举例说明。

一、“等时圆”的基本规律

1.如图1 所示,A为竖直平面内圆周上的最高点,B、C、D、E、F、…为圆周上的任意点,质点从A点沿不同的光滑斜面AB、AC、AD、AE、AF、…由静止开始下滑,到达斜面底端所用的时间都相等。

图1

2.如图2 所示,A为竖直平面内圆周上的最低点,B、C、D、E、F、…为圆周上的任意点,质点从B、C、D、E、F、…各点沿光滑斜面BA、CA、DA、EA、FA、…由静止开始下滑,滑至A点所用的时间都相等。

图2

例1 如图3 所示,光滑细杆BC、DC和AC构成矩形ABCD的两邻边和对角线,已知三根细杆的长度之比为1∶3∶2,细杆AC竖直。每根细杆上分别套有一小球a、b、d,三个小球的质量之比m1∶m2∶m3=1∶2∶3。现将三个小球同时从各细杆的上端由静止释放,不计空气阻力,则这三个小球沿各细杆滑行的时间之比为( )。

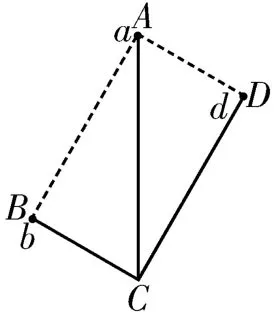
图3

A.1∶1∶1 B.1∶3∶2

C.1∶4∶9 D .1 ∶3∶4

因为ABCD为矩形,所以A、B、C、D四点必定在以AC边为直径的同一圆周上。三个小球同时从各细杆的上端由静止下滑至C点,遵循“等时圆”的基本规律,因此三个小球必定同时到达圆周的最低点C。

答案:A

同学们若不能利用矩形的几何性质,得出“A、B、C、D四点必定在以AC边为直径的同一圆周上”这一结论,就不会联想到“等时圆”模型。本题也可以利用匀变速直线运动规律和自由落体运动规律,逐一求出a、b、d三个小球的滑行时间,但是相较于利用“等时圆”基本规律求解的过程既复杂烦琐,又容易出错。

二、“等时圆”的推广规律

1.如图4所示,A、B、C、D、E、F、…为竖直平面内圆周上的任意点,过其中较高的一点(不是最高点)的竖直线(虚线)可以把圆分割成优弧和劣弧两部分,质点从该点由静止开始沿不同的光滑斜面下滑,从劣弧一侧开始质点滑至离该点越近的点所用的时间越短,滑至离该点越远的点所用的时间越长。比如,质点从A点(不是最高点)沿不同的光滑斜面AB、AC、AD、AE、AF、…由静止开始下滑至斜面底端所用的时间大小关系为

图4

t1＜t2＜t3＜t4＜t5。

2.如图5所示,A、B、C、D、E、F、…为竖直平面内圆周上的任意点,过其中较低的一点(不是最低点)的竖直线(虚线)可以把圆分割成优弧和劣弧两部分,质点从圆周上比这个点高的其他点由静止开始沿不同的光滑斜面下滑至该点,从劣弧一侧开始质点出发位置离该点越近所用的时间越短,质点出发位置离该点越远所用的时间越长。比如,质点从B、C、D、E、F、…各点沿光滑斜面BA、CA、DA、EA、FA、…由静止开始下滑至A点(不是最低点)所用的时间大小关系为t1＜t2＜t3＜t4＜t5。

图5

例2 如图6 所示,AB、AC、AD是固定在竖直平面内的三根光滑细杆,A、B、C、D四点位于同一圆周上,圆内AE为水平线,细杆AB、AC、AD互成30°角,每根细杆上分别套有一质量均为m的小球。小球从细杆顶端由静止下滑到A点所用的时间分别为t1、t2、t3,则( )。

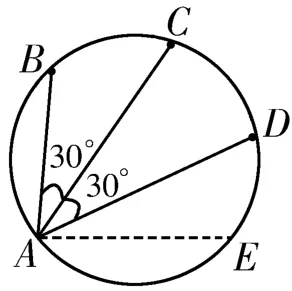
图6

A.t1=t2=t3B.t1＞t2＞t3

C.t1＜t2＜t3D.条件不足,无法判断

A点不是圆周上的最低点,小球从细杆顶端由静止下滑到A点,遵循“等时圆”的推广规律。与水平线AE垂直的线将圆周分割成优弧和劣弧两部分,从劣弧一侧开始,B、C、D三点距离A点越来越远,小球沿细杆AB、AC、AD下滑所用的时间越来越长,因此t1＜t2＜t3。

答案:C

本题也可以通过作辅助线,构建出与B、C、D三点分别对应的“等时圆”,先利用“等时圆”的基本规律找到与从B、C、D三点下滑所用时间相同的B′、C′、D′的位置,再根据B′、C′、D′三点与A点的位置关系,结合自由落体运动规律,判断出时间t1、t2、t3的大小关系。

1.如图7所示,在同一竖直平面内,一半圆的直径水平,与另一圆的底部相切于O点,O点恰好是下方半圆的圆心。三条光滑轨道AOB、COD、EOF的两端分别位于上下两圆的圆周上,三条轨道与竖直线O′O″的夹角关系为α＞β＞θ。现让一小物块分别从三条轨道的顶端由静止下滑至底端,所用的时间分别为t1、t2、t3,则( )。

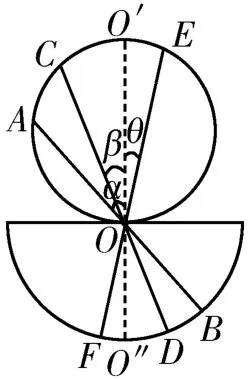
图7

A.t1=t2=t3B.t1＞t2＞t3

C.t1＜t2＜t3D.t1=t2＜t3

2.如图8所示,位于竖直平面内的固定光滑圆形轨道与竖直墙壁相切于A点,与水平面相切于B点,圆心为O,在圆形轨道内搭接有AB、AC两条光滑倾斜轨道,轨道AC与竖直墙壁间的夹角α=60°。现将质量相同的三个小球a、b、c分别放在轨道AB、AC的顶端和圆心O处,同时放手,让三个小球由静止开始运动(c球可以直接穿过轨道AC),则( )。

图8

A.a球最先到达B点

B.b球最先到达C点

C.c球最先到达B点

D.a、c两球同时到达B点

参考答案:1.B 2.C