利用不等式约束求解病态问题的新算法
赵邵杰 宋迎春 李文娜
(1. 中南大学 地球科学与信息物理学院, 湖南 长沙 410083; 2. 有色金属成矿预测与地质环境监测教育部重点实验室(中南大学), 湖南 长沙 410083)
0 引言
病态问题是大地测量的数据处理中常出现的棘手的问题,广泛存在于控制网平差、精密轨道解算、重力场向下延拓、变形监测、极化干涉合成孔径雷达(Polarimetric Interferometric Synthetic Aperture Radar,PolInSAR)植被参数反演等领域。病态问题法方程的条件数远大于设计矩阵的条件数,误差方程系数阵或常数向量的微小扰动,便会造成参数解剧烈变化,难以得到可靠的结果,主要原因是:系数阵出现了相对较小的奇异值,且最大与最小的奇异值相差了几个甚至十几个量级,这将导致计算过程中,未知参数的方差被较小奇异值过度放大,显著降低平差结果的精度[1]。在病态问题的处理上,目前有许多成熟的方法。如:岭迹法、GCV法(Generalized Cross-Vali-dation)、Tikhonov正则化法[2]、截断奇异值法[3]等。这些方法在一定的条件下可以降低平差模型的病态性,得到较可靠的平差结果,不足之处在于无法利用测绘工程中的先验信息。
根据未知参数的先验信息建立不等式约束,并同误差方程联合平差的方法,称为不等式约束平差法。这种方法补充了平差问题的信息量,对未知参数形成有效约束,深受国内外专家学者的广泛关注[4-15]。由于不等式约束的存在,它给平差问题的解算带来了一定的难度,在已有的文献中,许多学者重点研究了不等式平差模型的解算方法,然而,他们很少或者没有针对系数矩阵病态问题展开研究。如,在椭球约束算法[15]计算过程中,将不等式约束表示为椭球约束的形式,通过计算广义型岭估计得到平差结果,但由于转化过程会弱化不等式约束的条件,可能导致平差结果不在不等式约束范围内,从而严重影响参数解的精度,故这类方法受主观条件的影响较大。在有效约束算法[14]和规划类算法[11]计算过程中就有法矩阵求逆运算,或法矩阵的子矩阵求逆运算。当系数矩阵病态时,这些求逆运算就会出现异常,使得解产生严重的偏离。
当不等式约束作为一个先验信息纳入平差运算时,在病态的平差模型中可以增加一些虚拟的观测信息,这显然可以对观测信息进行补充,从而降低平差模型的病态性,使得平差结果更加可靠。这需要在构建不等式约束平差算法时,尽量避免对病态系数矩阵进行求逆运算,否则不等式约束信息还没有利用,其病态问题的影响已经在参数解中存在了。因此,避免对病态矩阵求逆是求解病态问题的一个较理想的途径。
本文针对未知参数具有不等式约束的情形,通过KKT(Karush-Kuhn-Tucker)条件将平差问题转化为线性互补问题(Linear Complementary Problem,LCP)[16-18],转换后的LCP的系数矩阵是非对称的、病态的,现有的平差算法无能为力。本文借助Lemke算法给出了针对非对称的、病态的LCP的一个算法,同时,为利用Lemke算法解决不等式约束平差问题提供了一个新的途径。新的算法不同于已有的不等式约束算法,在算法构建过程中完全避免了矩阵求逆运算,使得病态性在计算过程中对迭代解的影响大大降低。论文通过几个实例验证了算法在处理病态问题的有效性,丰富了利用不等式约束解决病态问题的算法。
1 病态性影响分析
平差模型
L=AX+e权阵P
(1)
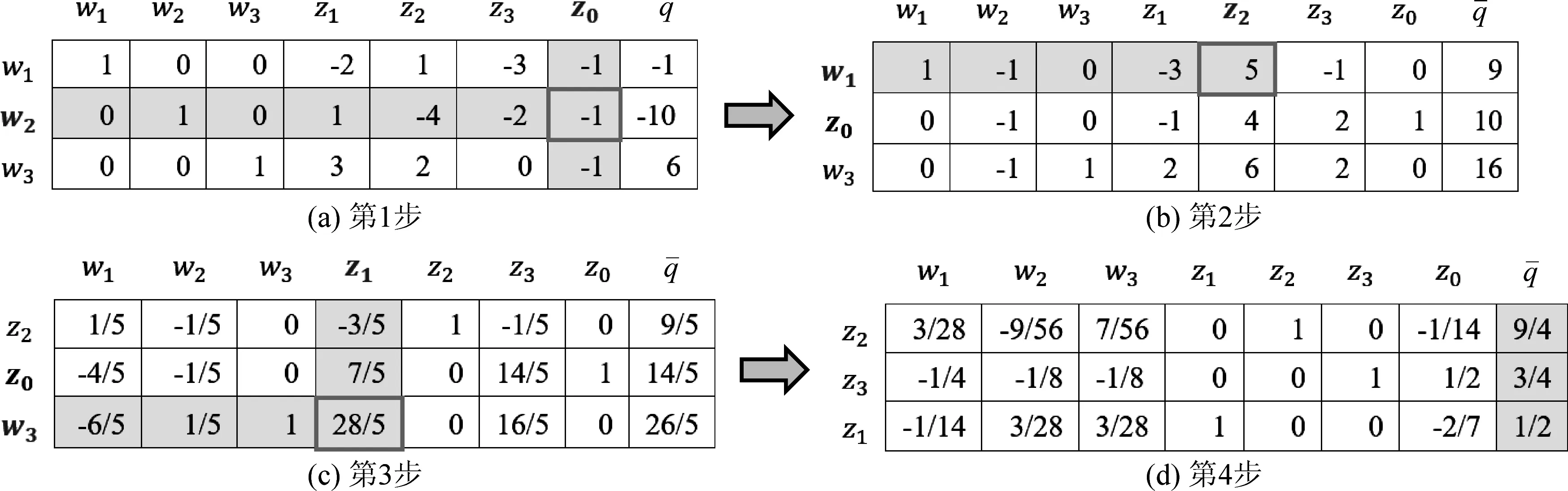
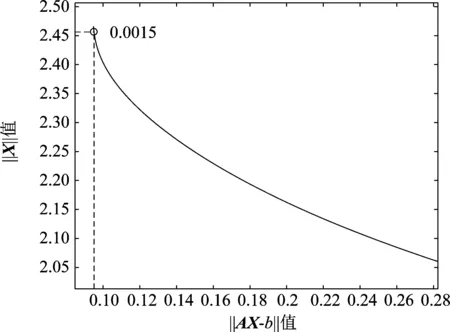
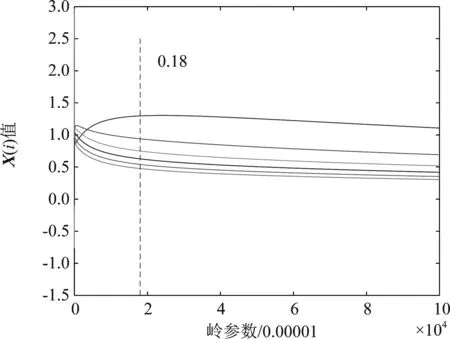
其中,A是m×n维的列满秩矩阵,rank(A) min ‖L-AX‖2 (2) 式(2)中,‖·‖2表示2范数。式(2)称为病态问题,在矩阵A无病态条件下,最小二乘解为 (3) 我们对病态问题的系数阵A进行奇异值分解 (4) (5) 其中,UA=[u1,…,um]是m阶的正交矩阵;GA=[g1,…,gn]是n阶的正交矩阵;n×n维的对角阵Σ=diag(λ1,λ2,…,λn),对角线元素为A的奇异值,且λ1≥λ2≥…≥λn≥0。 由于系数阵A病态,我们设λN1、λNn为法方程系数阵N=ATPA的最大奇异值、最小奇异值,则法方程系数阵的条件数为 (6) 统计应用经验表明,法方程条件数小于100时可以认为没有病态性;条件数位于100到1 000之间认为存在中等程度的病态性;条件数大于1 000认为存在严重的病态性[19]。若条件数cond(N)很大,即使N和L的扰动很小,求解式(3)时也会引起X很大的偏差。因此,改善病态问题的一个可行途径,就是避免对法方程中的不稳定(条件数很大)矩阵N求逆,增强解的抗干扰能力。 目前,病态问题的研究主要在两个方面,一是对平差模型进行诊断,判断是否病态;另一方面是研究病态问题的解算方法,例如:正则化方法,截断/修正奇异值方法。附加约束方法等确定性方法和随机方法。下面,我们将对求解病态问题的新算法进行研究。 最小二乘平差准则为 minf(X)=(L-AX)TP(L-AX) (7) 因在目标函数(L-AX)TP(L-AX)=XT(ATPA)X-2LTPAX+LTPL,LTPL是一个常量,故可以把式(6)转化为一个二次规划问题 (8) 式(7)中,c=-(LTPA)T为n维的列向量,N=ATPA为n×n维的对称正定矩阵,故f(X)是严格凸二次函数,即f(X)的局部最小值为全局最小值。我们将先验信息表示为不等式约束GX≤h,X≥0,其中,G为s×n维的行满秩矩阵,h为s维的列向量,并联合式(1),得到具有不等式约束的病态模型 L=AX+e权阵P (9) s.tGX≤h,X≥0 (10) 此处,没有把式(10)中的两个不等式合成一个不等式,是为了便于式(8)和(9)的转换。由上面的分析可知式(8)和(9)可转换为如下的二次规划问题(Quadratic Programming): (11) s.tGX≤h,X≥0 (12) 二次规划问题是非线性规划中一种特殊的情形,典型的算法有:Lagrange方法、起作用集方法、路径跟踪法、Wolfe算法等[22-23]。前三种方法无法回避对病态矩阵求逆,Wolfe算法应用广泛,却要求N半正定,故不适用于常规的病态问题。因此,寻找一种不求逆的、大多数情况适用的解算方法是很有必要的[20],由于Lemke算法既可避免对病态矩阵求逆,又可处理N正定和半正定情形,故本文深入研究了这种方法在病态问题中的应用。 本文利用不等式约束求解病态问题,需将已得到的二次规划问题转化为LCP,再结合Lemke算法求解。由于A列满秩,其法方程系数阵N是一个正定矩阵,f(X)为严格凸二次函数,故函数的局部最小值也是全局最小值,K-T点是式(10)和(11)的最优解。根据Karush-Kuhn-Tucker条件 NX+GTY+c-u=0,v=h-GX≥0 (13) vTY=0,uTX=0 (14) u≥0,v≥0,X≥0,Y≥0 (15) 式(10)整理得 (16) (17) MZ+q≥0,Z≥0,ZT(MZ+q)=0 (18) 其中,M∈R(s+n)×(s+n)是非对称矩阵;q∈Rs+n;Z∈Rs+n。 式(9)到式(18)的推导,目的是把不等式约束条件下的病态模型转化为线性互补问题求解。式(18)的等价形式为 w-MZ=q,w≥0,Z≥0,wTZ=0 (19) 由于M是非对称的、病态的矩阵,利用一般的线性互补问题算法是不能求解式(18)的。对于式(19)需要研究特殊情形的线性互补问题,如非对称LCP,秩亏LCP等,因此,这些算法直接移植到测量平差中来是非常复杂的,从式(16)和(17)可以看出,w和Z不仅要满足m+n维未知变量的线性方程组,而且要保证wTZ的内积为零。1962年,Lemke基于单纯型算法的思想,提出了求解线性互补问题式(19)的Lemke算法。这种算法建立在表1的基础上,可用于处理非对称的LCP,输出的结果完全符合式(19)解的性质。由于表1中只含有一个线性方程组的系数矩阵,没有对应目标函数的系数向量,故它在结构上比线性单纯形表的设计更为简单。下面,给出了该算法的具体步骤[24]。 表1 线性互补问题对应的单纯形表 第1步将线性互补问题的系数阵M和向量q写入一个单纯形表中。若单纯形表的最右列q的分量非负,即q≥0,停止计算。否则,添加人工变量z0,使之对应的系数为-1,并将该列写于q的左边一列。 第2步将q中对应负数绝对值最大的元素所在的行作为主行,选取z0中主行上的元素作为 主元消去的元素,进行主元消去,并记录此时w出基变量的序号。 第3步设出基变量为ws(或zs),则要求下一次必须zs(或ws)将作为进基变量。主元消去元素应在该列中选取,其对应的主行r应满足: (20) 其中,dj为当前表中即将进基变量所在列对应的第j个分量;pj为当前单纯形表最右列q对应的第j个分量。 第4步进行主元消去,若此时人工变量z0出基,转第6步;否则,第5步。 第5步记录主元消去的出基变量的序号,转第3步。 第6步输出对应的最优的平差结果Z=(X,Y)T。 算法步骤分析,以下面方程组为例 (21) 算法示意图分析: 图1(a)→(b)为第1步至第2步的过程:建立Lemke算法表,首先根据q的负数绝对值最大的元素“-10”确定z0列的主行元素w2,接着w2出基z0进基,并进行主元消去。根据式(14)定位第3步将主元消去的位置,即(w1,z2)。 图1(c)→(d)为第3步至第6步的过程:在对(w1,z2)进行主元消去后,w1出基z2进基,我们发现z0并未出基,故根据式(20)重新定位第3步主元消去的位置(w3,z1),进行主元消去,w3出基z1进基。接着重复第3步定位主元消去的位置,完成进基、出基的过程,直至z0出基,图1(d)展示了算法结束时的状态。根据Lemke算法表,我们得到了LCP的互补可行解 (22) 图1 Lemke算法示意图 由于Lemke算法应用不等式约束解病态问题过程,并未涉及到对病态矩阵的求逆运算,故平差结果不会受到病态矩阵求逆的影响,保证了未知参数X的稳定性;在二次规划式(13)中,法方程系数阵N是正定矩阵,二次规划为严格的凸二次规划,因此,保证了未知参数X的唯一性[20]。综合未知参数具有稳定性和唯一性的特点可知,用Lemke算法求解不等式约束病态问题是一种理论清晰、目的明确的新方式。岭迹法、GCV法、L-曲线法等是大地测量数据处理中,使用频率很高的处理病态问题的算法,但它们无法回避对病态矩阵的求逆,岭估计方法虽然可以应用到病态矩阵的求逆问题,但岭参数的确定方法是人为的方法,无法利用未知参数X的先验信息,因此,存在着局限性。Lemke已在测绘数据处理中得到应用[11],这些应用主要还是针对不等式约束的算法研究,而不是针对病态问题进行研究。下面,结合两个模拟算例进行实验分析,验证Lemke算法的有效性。 Hilbert矩阵是经典的病态矩阵,定义为 (23) (24) 图3 L-曲线法示意图 图4 岭迹法示意图 从平差结果可以看出,由于系数矩阵的高度病态性,使得最小二乘解XLS严重失真,‖XLS-Xreal‖的值高达3.418 3×1011;方法1和方法2虽然利用了未知参数X的先验信息GX≤W,在一定程度上提高了解的精度,却未能改变平差模型AX=L的病态性,因此,平差的结果也严重失真。 表2 几种算法的平差结果比较 根据GX≤h,X≥0,将先验信息Δx≤2.3 m,Δy≤4.0 m,Δz≤6.8 m,表示为不等式 表3 系数矩阵和观测向量 单位:m 表4 GPS快速定位的算法结果与比较 单位:m (25) 从表4的平差结果,可以得出以下的结论: (1)在本算例中,法方程的条件数为cond(N)=2.480 9×109,因此,法方程严重病态。此情况下,按最小二乘的准则对法方程进行求逆运算,必然会导致未知参数的解不稳定,实验结果也验证了最小二乘解严重偏离未知参数的真值。 (2)GCV法、L-曲线法、岭迹法均未利用到未知参数的先验信息,故未得到理想的平差结果。岭迹法相对于其他两种方法,偏离真值的程度要大得多,一方面与岭参数在选择上受主观意识影响较大有关,另一方面也与数据结构有关。对于不同的数据,岭估计对病态问题的改善程度也是不同的。 (3)方法1和方法2属于广义型岭估计,具有一定的主观性。从平差结果可以看出这两种方法均未克服法方程的病态性,方法2在观测数据和约束条件理想的条件下,也可以在一定程度上对参数解改善。 (4)本文提出的不等式约束病态平差模型的Lemke算法充分利用了先验信息,对未知参数形成了有效约束,平差结果同真值最为接近且效果最好,显示出了这种算法的优越性。 大地测量中,未知参数的先验信息反映了被测目标的几何或物理特征、内在相关性、测量精度等,在数据处理中,结合有效的先验信息以等式或不等式约束的形式进行平差,可以补充观测信息的不足,对未知参数形成约束,有效提高参数估计的效率。本文针对病态问题,提供了一种新的平差方法——Lemke算法。本算法没有涉及病态矩阵N=ATPA的求逆,因此,A的病态性对Lemke算法影响不大,有效抑制系数矩阵的复共线性,降低解的不稳定性。其次,Lemke算法在构造上简明易懂,充分利用测绘工程中的先验信息解决病态问题,降低了平差模型的复杂性,丰富了病态问题的算法理论。2 不等式约束病态模型与Lemke算法
2.1 不等式约束病态模型
2.2 线性互补在平差问题中的应用
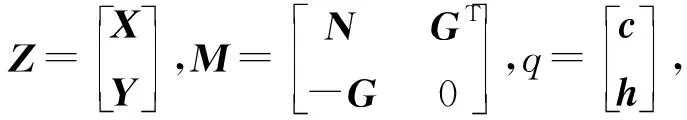
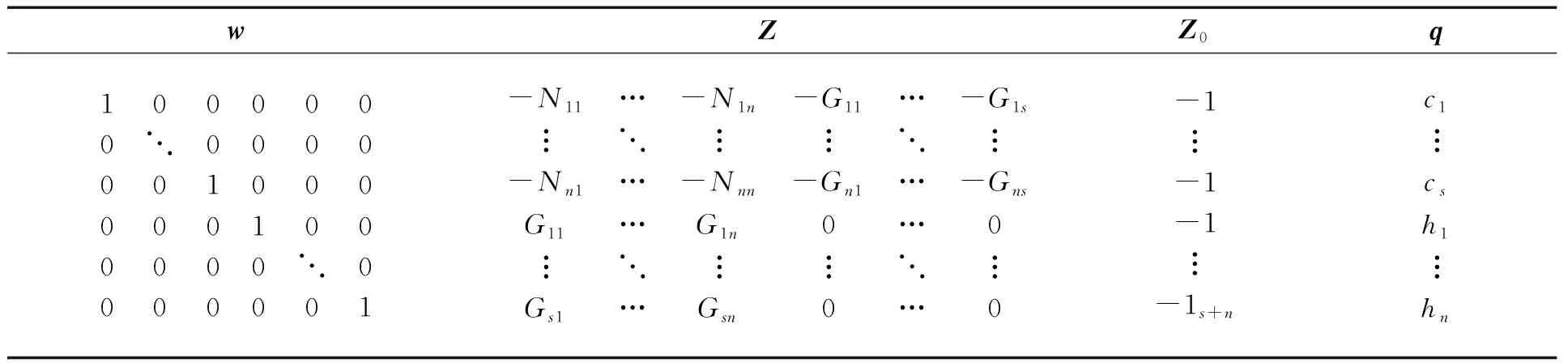
2.3 Lemke算法步骤
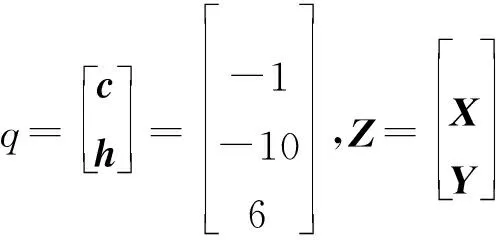
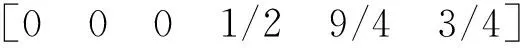
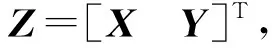
3 算例1



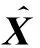
4 算例2


5 结束语

