关于混凝土坝应力监测应变计组应变不平衡量调整

卢正超，芦绮玲，王 雪，刘学强

（1.流域水循环模拟与调控国家重点实验室，北京 100038；2.中国水利水电科学研究院 水电中心，北京 100038；3.山西省水利发展中心，山西 太原 030002；4.邵东市邵水管理所，湖南 邵阳 422800）

1 研究背景

高混凝土坝的应力问题一直是大家关注的重点［1-2］。根据我国现行的混凝土坝监测技术规范，对于1级混凝土大坝来说，混凝土应力应变观测为必设项目。混凝土应力应变观测的目的是了解坝体的实际应力分布，寻找最大应力（拉、压应力和剪应力）的位置、大小和方向，评价大坝的强度安全程度，为大坝的运行和加固维修提供依据。我国新建的高混凝土坝，特别是拱坝，布置了数量众多的应变计组。如：二滩拱坝［3］（H=240 m）布置了41组应变计组（6向29组，3向6组，2向35组），小湾拱坝［4］（H=294.5 m）布置了148组（9向57组，7向73组，5向18组），溪洛渡拱坝［5］（H=284.5 m）布置了145组（6向69组，5向66组，3向10组），乌东德大坝［6］（H=270 m）布置了68组（9向24组，7向38组，2向6组）。

应变计（组）观测混凝土应力应变本身具有很多干扰因素，导致观测成果的精度长期以来存在较大争议。利用应变计组测值计算混凝土应力的基本假定是，同组的应变计（及无应力计）应符合点温度条件和点应力条件。点温度条件指的是，同组的应变计（及无应力计）同测时温度测值的极差应在误差范围之内，工程上一般按1℃控制。点应力条件指的是，同组各应变计同测时的应变测值应满足弹性力学第一应变不变量原理，即某点互相垂直的三向正应变之和，不因选择的方向改变而改变。所谓的应变不平衡量，从数学上来说是多余观测带来的不满足第一应变不变量原理的量；从物理上来说，应变不平衡量产生的原因很多，不只是观测误差引起的，还有诸如应变计组的各支应变计并不真正在一个“点”上，埋设时不能保证应变计的轴线在空间上两两垂直等因素。因此，应变计组应力计算中很重要的一个步骤是应变不平衡量的检查和处理。不平衡量调整的目的，主要为了合理地分配误差，得到应变的最或是值，提高观测精度。经验表明，应变计组的应变不平衡量，由于各种原因最大可能达到20 με～30 με左右，这相对于大坝混凝土最大100 με左右的拉应变来说是很可观的，不合适的处理可能引入不必要的系统性偏差。但从此前流行甚广的专业书籍［7-8］和近年发表的一系列期刊文章或学位论文［9-17］来看，应变不平衡量处理存在一些不尽合理甚至错误的做法：

（1）储海宁［7］给出了4向和9向应变计组应变不平衡量调整的公式，朱赵辉［9］等针对7向应变计组给出了类似的公式，但二者均未给出理论依据，基本是按照一个平面内的四支应变计平分其不平衡量，7向、9向应变计组的不平衡量调整公式不满足各支应变计应变不平衡量调整（或称改正数）平方和最小的原则。文献［7，10-12］等采用了与此相同的公式。

（2）郭晨［13］利用最小二乘法给出了7向应变计组应变不平衡量调整的公式。但在构造最小二乘函数时，实际上将共用的应变计重复计算了一次。鉴于7向应变计组这一测量体系只有同精度的7支仪器，共用的应变计只是因其位置特殊，其测值用于两个平面的计算，重复计算相当于提高了其精度指标，于理无据，因此其给出的改正数公式不能认为是正确无误的。此公式被文献［14-15］直接或间接引用。

（3）黄浩［16］利用最优化平衡法进行应变计组平衡，某种程度上将问题复杂化了，在数学上实际上和文献［13］的最小二乘方法一样。文献［17］的五向应变计组不平衡量修正公式有误。

本文利用条件平差的有关算法，来统一处理各向应变计组的不平衡量调整问题。

2 应变计组的常见结构型式

国内混凝土大坝工程中常用的应变计组的结构型式有4向、5向、7向和9向，如图1所示。多向应变计组一般安装在如图2（a）所示的球形组合安装支架上，锦屏一级大坝则采用了一种新型的如图2（b）所示金字塔形支架［11］，支架由6 mm直径钢筋焊接而成，改进了前者易受到施工破坏且方向难于保证的问题，值得推广应用，其5向和9向应变计组布置见图3（拓扑结构实际上和图1（b）、图1（d）等价）。二滩大坝采用了2向、3向、6向应变计组，分别用于坝体上、下游面和内部应力监测。

图1 应变计组常见结构型式

图2 9向变计组安装支架

图3 锦屏一级大坝应变计组埋设示意图

3 应变计组应变不平衡量调整的传统方法

混凝土内部任一点的空间应变为二阶张量，具有6个独立的应变分量，而同一平面内独立的应变分量有3个。对于前述4向（或5向）、7向和9向应变计组，分别有1个、2个和3个平面内布置了有4支应变计（平面内间隔成45°角），存在多余观测。按第一应变不变量原理，理论上同一平面内两两轴线互相垂直的4支应变计（s1与s2互相垂直，s3与s4互相垂直，参见图1（a）或图1（b））的应变值应满足下述条件：

实际上，由于混凝土并非理想的均匀连续介质以及观测误差的存在，上式往往不能成立，而存在不平衡量Δ1。

应变计s1～s4的改正数δ1～δ4如下式（3）：

对于图1（c）中的7应变计组，不平衡量为公式（4），其中Δ1、Δ2为不平衡量，应变计s1～s7的改正数δ1～δ7如下式（5）：

对于图1（d）中的9应变计组，不平衡量为式（6），其中Δ1、Δ2、Δ3为不平衡量，应变计s1～s4的改正数δ1～δ9为式（7）：

上面的式（3）、式（7）与文献［7］一致，式（5）与文献［9］一致。

4 基于条件平差算法的不平衡量调整

4.1 条件平差算法 在测绘学中，利用基于最小二乘原理的条件平差法对多余观测带来的闭合差进行检查和处理，其主要目的是消除观测值中的矛盾，合理分配误差，求出观测值或其函数的最或是值，提高观测精度［18］。应该明确指出，应变计组的不平衡量调整问题，数学上与条件平差问题是完全等价的。下面采用条件平差算法对各向应变计组的不平衡量调整进行统一的处理。采用以下符号：

设有n个应变测值为：s1，s2，…，sn

调整以后的应变值（最或是值）为：ε1，ε1，…，εn

各测值的权为：P1，P2，…，Pn

各测值的改正数为：δ1，δ2，…，δn

r个条件方程的应变不平衡量（或称改正数，相当于测绘学中的闭合差）为：Δ1，Δ2，…，Δr

设A为条件方程的系数矩阵，D为改正数矩阵，E为不平衡量矩阵，S为应变测值矩阵，即：

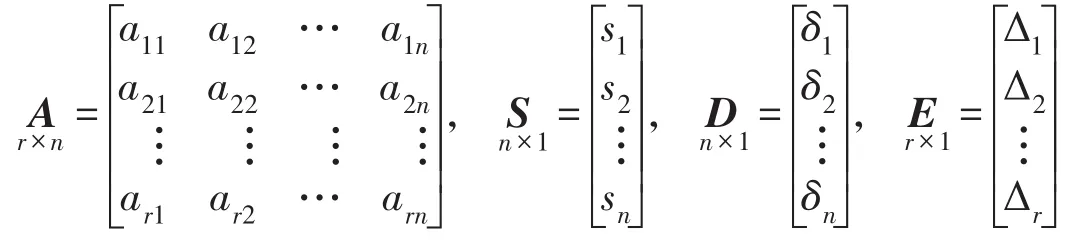
根据第一应变不变量原理，得到r个条件方程：

r个不平衡量满足下式：

从而得到r个条件方程的矩阵形式：

鉴于n＞r，式（10）的解不唯一。我们需要的是改正数平方和[pdd]=min（最小）的唯一一组改正数：δ1，δ2，…，δn。根据求条件极值的原理，设函数

为求函数Φ的极值，对上式（12）的变量D求一阶偏导，并令其为零，求解得到：

将式（13）代入式（10），并设过渡矩阵

得到联系数矩阵：

将式（15）带入式（13），注意到N为对称矩阵，即可求解得到改正数矩阵：

对上述推导细节感兴趣的读者，可参阅文献［18］。

4.2 九向应变计组应变不平衡量改正数 假定各应变计等精度，权矩阵P为单位矩阵。考虑图1（d）中的九向应变计组，根据其不平衡量方程（6）得到系数矩阵A：

将式（17）带入式（14）得到过渡矩阵N，进而得到：

改成工程上常用的形式即：

得到调整后的应变值：εi=si+δi，i=1，…，9。

4.3 七向应变计组应变不平衡量改正数 同样假定各应变计等精度，权矩阵P为单位矩阵可略去。采用与上述相同的方式进行演算，考虑图1（c）的七向应变计组，利用其不平衡量方程（4）得到系数矩阵A：

将式（20）带入式（14）得到过渡矩阵N，进而得到：

改成工程上常用的形式即：

得到调整后的应变值：εi=si+δi，i=1，…，7。

4.5 几点讨论 根据上面的演算结果，讨论如下：

（1）传统的应变不平衡量调整式（5）和式（7）的基本思路是按照一个平面内的四支应变计平分所在平面内的不平衡量，没有明确的数学基础，不满足应变不平衡量改正数平方和最小的原则，对于不完全相同的两个平面共用的应变计，其改正数（如公式（5）和（7）中的δ1、δ2和δ3）属强令相等取平均，没有顾及应变计组中各应变计的空间相对位置关系，其他各支也同样存在数学处理与物理意义不符问题。

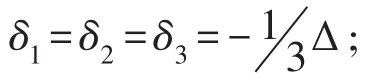
（3）从一般意义上来说，式（19）和式（22）中代数表达式的结构清楚地表明，改正数与应变计组中各应变计的空间相对位置关系有关：对于两个平面共用的应变计，其改正数关于两个平面的不平衡量对称；仅在一个平面内的应变计，其改正数关于另外两个平面的不平衡量对称，显然具有清晰的物理意义。

（4）鉴于式（19）和式（22）中各应变计的改正数与应变计的空间相对位置关系有关，对于编号与图1中编号顺序不同的应变计组来说，需要调整编号顺序。为避免混淆或符号错误，基于物理概念，可采用下述方法（利用前述算法数学上可严格证明，因篇幅所限，此处略去）：对9向应变计组，以图3所示锦屏一级大坝的九向应变计组为例，首先写出不平衡方程：

（5）若应变计组中的某支或某几支存在测值异常，不可直接套用式（19）和式（22），而应该根据具体退化后剩余的不变量个数的情形而定，选择7向或5向的调整式（以及下述8向或6向调整公式）或不进行调整。比如，图1（d）中所示九向应变计组的s8或s9损坏数据不可用，则式（6）中第3式无意义，s8和s9不能进行平差调整，其他各支按7向的公式进行调整；图1（d）中所示九向应变计组两平面共用的s1损坏数据不可用时，平差调整按下式进行（可视为8向应变计组平差调整）：

其中，s1可以通过平面内插补得到。其他各支损坏的公式可类推。对于图1（c）中所示七向应变计组的s3损坏数据不可用时，平差调整按下式进行（可视为6向应变计组平差调整）：

其中，s3可以通过平面内插补得到。图1（c）中所示七向应变计组的损坏s3以外的1支，按5向的公式进行调整。其他各支损坏的公式可类推。

（6）对于前述2向、3向、6向应变计组，因为没有多余观测，不存在不平衡，自然也就没有不平衡量调整的问题。

5 结论

本文利用条件平差的有关算法处理多向应变计组的不平衡量调整问题，得到如下结果：

（1）应变计组的不平衡量调整与测绘学的条件平差问题在数学上完全等价，利用其算法得到的9向、7向应变计组的应变不平衡量调整公式，与目前习用的公式相比，具有更严格的数学基础和更明确合理的物理意义，有助于提高混凝土应变监测的数据质量。

（2）首次得到9向、7向应变计组因无效及故障失效退化后的8向、6向应变计组的应变不平衡量调整公式。

（3）该方法也可用于研究不等精度测量问题。

（4）在应变不平衡量调整改正数计算前，应检查同组的应变计是否满足点温度和点应力条件。对不满足点应力条件的应变计组，应检查各支应变计是否异常或存在系统误差；存在系统误差的应变计，视为无效仪器。根据应变计组退化情况（排除无效及故障失效仪器），具备平差条件时，应用本文给出的相关公式对剩余的正常工作的应变计进行应变不平衡调整计算。