实时多聚焦显微图像融合算法
(1.浙江工业大学 计算机科学与技术学院,浙江 杭州 310023;2.浙江在线 新闻中心,浙江 杭州310039;3.浙江中控技术股份有限公司 研发中心,浙江 杭州 310052)
显微镜在生物医疗、工业界等不同领域有着广泛的应用,因为显微镜平台高倍率条件下景深很小,难以观看样品全貌,所以需要研究多聚焦显微镜图像融合问题。目前,针对图像融合问题已经有很多研究[1],然而多聚焦显微镜图像需要细节表现力强的算法,以保证融合图像的质量,目前多聚焦显微镜图像融合仍是一个挑战性难题。
针对图像融合的研究广义上主要可以分为两类:基于变换域的方法和基于空间域的方法。基于变换域的方法主要使用金字塔分解、小波变换和多尺度几何分析。这些方法包括拉普拉斯金字塔[2]、梯度金字塔[3]、离散小波变换[4]、对偶树复小波变换[5]、曲波变换[6]和ND滤波[7]等。基于变换域的多焦点图像融合方法的基本框架是:首先将源图像分解为一个多尺度域,在多个尺度上进行合成,然后通过反变换对融合后的图像进行重构。变换域的选择很重要,高频低频域的融合规则也很重要。基于空间域的方法通过融合聚焦度量方法直接估算图像的锐度。一般来说,其可进一步分为基于像素[8-10]的方法和基于块[11-12]的方法。这两类方法各有优缺点,基于像素的方法虽然可以显著提高融合后图像的视觉效果,但是它对噪声极其敏感,因为噪声点处也有高频信号,导致合成图像空间上不连续,文献[13]使用块的一致性校验,文献[14]使用去除面积小于1%的块以得到更连续的融合结果,不过在不同类型图像中需要调整参数才能得到较好的结果。基于块的方法通常将图像分为M×N块,通过分块计算块的锐度,可有效避免少数噪声点带来的影响,但是此类方法容易产生块状效应,且块的大小对融合结果的影响很大。因为空间域的方法是直接估算图像锐度,所以聚焦度量方法在此处很重要。通常通过计算图像的梯度能量(EOG)、拉普拉斯能量(EOL)、改进拉普拉斯和(SML)、空间频率(SF)和方差等来度量图像的聚焦程度。近些年由于深度学习的发展,又出现了各类通过训练神经网络进行融合的方法[15-18],其思路与传统方法一致,只不过使用神经网络决策得到聚焦度量,一般有将整幅图像作为输入、将图像切分为多个块进行输入以及将边缘检测后的图像进行输入等,输出一张决策图或者某一点的聚焦结果。基于神经网络的方法虽然在多数图像上可以获得很好的效果,但是由于存在大量的参数,计算复杂度很高,难以用于实时应用场景。针对上述问题,笔者提出了一种快速多聚焦图像融合算法。该算法采用拉普拉斯金字塔分解的同时,利用一种聚类算法来引导金字塔图像的融合。实验结果表明:算法可以有效提高融合图像的连续性,减小噪声带来的影响,并很好地保留图像的细节特征。此外,算法多处采用了积分图像的思想,大大提高了计算性能,在高分辨率下也可满足实时融合的应用场景。
1 算法概述
在实时系统中,算法的输入为相机数据流,当前输入的图像与上一张相似度很高时应不参与融合,由于在体视显微镜下序列图像存在较大程度的偏移,所以融合前还需要进行图像配准,配准完成后再进行图像融合。算法流程图如图1所示。

图1 算法流程图Fig.1 Flow chart of algorithm
2 算法细节
2.1 图像配准
针对图像配准有基于灰度模板和特征点的算法。基于灰度模板的算法主要通过灰度匹配,使用误差函数来判断匹配程度;基于特征点的方法有SIFT,SURF和ORB等,此类方法基本思想是:首先找出图像中稳定的关键点,根据特征点给它一个向量用于描述,然后通过这个描述进行特征点的匹配,估计出图像的变换矩阵。然而,在显微图像融合的应用场景中有如下两个特殊之处:
1) 由于光源是稳定的,视角是固定的,不会有透视变换和旋转,只会有位移以及光圈弥散,即视觉上的轻微放大。大量实验表明光圈引起的放大不会对图像有显著影响。
2) 由于聚焦的变化,特征点检测也会有较大的变化,假设有两幅图像,第1幅图像左半边比较清晰,右半边比较模糊,第2幅图像则相反,左半边比较模糊,右半边比较清晰,这时候在进行图像配准时,用基于特征点的方法会发现第1幅图像找出来的特征点集中在左边,而第2幅图像特征点集中在右边,此时特征点匹配会比较困难。同时,由于基于特征点的方法可以应对相机各种类型的变换,如平移、缩放、旋转和透视等,所有的这些参数组合进算法中,使得算法的复杂度提高,计算量巨大,不太适用于实时应用程序。因此,笔者采用了基于多级下采样与最大相关性方法,由粗到精进行匹配,大大减少了计算复杂度。
2.2 聚焦度量
对于多焦图像融合,需要先对图像进行聚焦度量,再对聚焦区域进行分割和图像融合。因此,选择合适的聚焦度量方法对后续过程至关重要。笔者分析了几种典型的度量方法:EOG,EOL,SF和SML。
EOG的计算式为
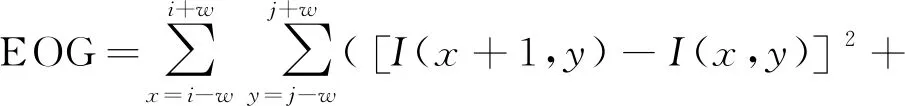
(1)
式中:I为源图像;w为窗口大小;(i,j)为窗口中心位置。
EOL和SF的计算式分别为

(2)
(3)
式中:RF为行频率;CF为列频率。其计算式分别为
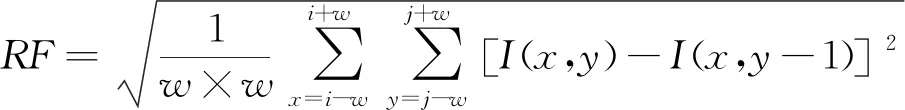
(4)
(5)
SML的计算式为

(6)


(7)
4 种聚焦度量方法只有SML在计算完每个像素点的锐度之后进一步考虑了邻域内的锐度信息,因此使用SML可以获得更好的融合结果。如图2所示,除SML外,其他方法的融合均出现了不同程度的白色伪影,并且采用SML方法能保留更多的细节。因此,笔者采用SML作为聚焦度量方法,并使用积分图像进行优化。

图2 不同聚焦度量方法融合结果对比Fig.2 Comparison of the fusion results by different focus measurements

图3 积分图像计算示意图Fig.3 Schematic diagram of integral image calculation
SML(x,y)=S(A)+S(D)-S(B)-S(C)
(8)

2.3 掩膜图像
因为聚焦的图像拥有更大的锐度,所以图像SML(x,y)越大则它的锐度越大,初始的掩膜图像M0计算式为
M0(x,y)=argnmax|SMLn(x,y)|-1n∈[1,2]
(9)
因为M0易受到噪声的影响,导致某些位置的掩膜图像数据错误,影响融合结果的连续性,所以通过对以R为半径的窗口内的类别进行聚类以提高连续性,图像对比如图4所示。图4(a)为聚类前的掩膜图像,图4(b)为经过聚类修正后的掩膜图像,可以看到修正后的图像中很多小的颗粒都消失了,表明使用聚类后的掩膜图像可以得到更连续的融合结果。

图4 聚类前后掩膜图像对比Fig.4 Comparison of the mask images before and after clustering
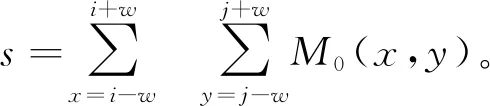
(10)
因为M0中只包含0和1,所以可以先计算M0的积分图像,积分图像计算方法见2.2节,然后只需要通过3 个加法计算就可以得到s。此时mask(x,y)等于0或1则代表该点是一个种子点,进而对每个种子点执行运算,把周围的点归到簇中,运算公式为
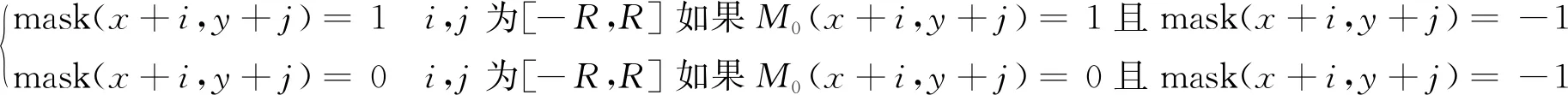
(11)
式中:x,y为mask图像每个种子点的坐标位置。将未归类的点,即mask图像中为-1的点归到最近棋盘距离的簇中,距离度量计算式为
d=max(|x1-x2|,|y1-y2|)
(12)
至此,mask为一张只有0和1的二值图像,每个点代表聚焦程度更高的图像索引。
2.4 拉普拉斯金字塔图像融合
首先进行高斯金字塔的分解,高斯金字塔中的图像由源图像通过高斯滤波并以去掉偶数行列的下采样方式得到,故下一层图像的大小永远是上一层图像的1/4,其中:Gl为高斯金字塔中的第l层图像,G0为原始图像。具体计算式为

(13)
式中:n为最大金字塔层数;Rl,Cl分别为第l层金字塔图像的行和列数;w为高斯核,其计算式为
(14)
由于在采样的过程中已经丢失了一些信息,为了在之后合成时减少这些信息的丢失,所以需要将这些信息保存下来,这些信息就形成了拉普拉斯金字塔。
然后将上一层的图像行列扩张为两倍,新增的行列以0填充,再使用先前的卷积核乘以4对图像作卷积,计算式为

(15)
新的图像与下一层的原图相减即为拉普拉斯金字塔保存的丢失信息,计算式为
(16)

(17)
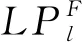
(18)

3 实验结果与分析
实验中,分别采用LP[2],GFF[8],DCT[11],ECNN[15]以及笔者方法对3 组图像进行融合测试,除笔者方法外的其他实现均来自于公开的代码,实验运行环境为i5 8400的CPU+8 G内存,操作系统为Win 10,使用C++实现。
3.1 实验数据和误差度量方法
为了比较的一致性,样本配准后对融合结果进行比较。总共有3 组图像(包括2 组电路板与1 组植物切片),电路板每组有5 张不同焦面且尺寸为5 472×3 648的24 位真彩色图像,样本数据如图5,6所示。因为植物切片是一个斜面,所以序列图像较多,共11 张,取序列中第1,3,5,7,9,11张图像,如图7所示。图5,6采集于体视显微镜,可以直观地看出立体的形态。图5的焦面从顶部往下依次变化。图6的焦面从底部往上依次变化。图7采集于生物显微镜,景深很小,由于植物切片崎岖不平,焦面分散在图像的各个区域。

图5 样本1电路板Fig.5 PCB of sample 1

图6 样本2电路板Fig.6 PCB of sample 2

图7 样本3序列部分图像Fig.7 Sequence of partial images of sample 3
采用方差和信息熵来度量融合质量,方差公式为
(19)


(20)

3.2 可视化比较和分析
对于样本1与样本2,由于只有5 张序列图像,且焦面之间区分明显,因此大部分区域融合质量接近,其他方法在不同区域的细节处均存在一些问题,尤其是DCT方法,在样本1与样本2的融合结果里均出现了大量错误的伪影,单独以矩形标出,如图8与图9(a)所示。对于样本3,由于生物显微镜下细胞切片可以被透视,很多区域没有一个固定的焦面,即多聚焦图像序列中某些区域没有哪一处是非常清晰的,因此需要从多张图像的失焦区域融合成相对清晰的结果,此类场景对于单纯使用一张mask图像来指导融合的方法(如DCT,GFF与ECNN等)是做不到的,所以针对样本3,笔者方法可以得到更多的细节,与其他方法对比明显,结果如图10所示。

图8 样本1的融合结果Fig.8 Fusion results of sample 1

图9 样本2的融合结果Fig.9 Fusion results of sample 2

图10 样本3的融合结果Fig.10 Fusion results of sample 3
为了进一步定量分析融合后的结果,采用方差、信息熵对每组融合图像进行客观度量,计算结果如表1所示,由表1可以看出笔者方法均获得了最佳度量结果。

表1 样本1,2的电路板以及样本3的植物切片融合结果对比
算法运行效率如表2所示,由表2可以看出:随着图像分辨率的增加,笔者算法运行时间虽然在增加,但是即使在1 600 W这种高分辨率情况下,运行时间也只有511 ms,而如果不采用积分图像的方法,算法效率明显低很多,特别是当分辨率达到1 600 W时,所需时间超过95 s,无法支持实时计算。DCT,LP,GFF和ECNN方法均采用作者提供的源码进行实验,编程语言为Python/Matlab,笔者方法采用C++作为实现语言,由于ECNN方法作者提供的源码在600 W 分辨下测试便运行了数小时,因此不作运行效率参考。
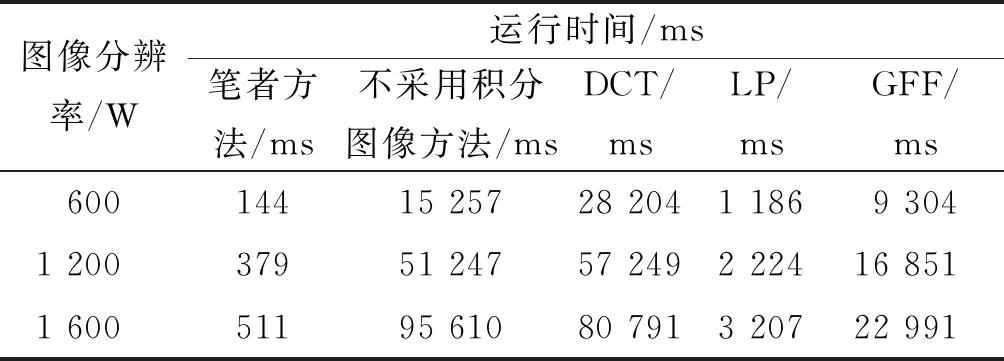
表2 算法运行效率Table 2 Efficiency of algorithm
4 结 论
笔者提出了一种实时多聚焦图像融合算法,实验结果表明:一方面,该算法能有效抑制伪影,且在不同场景下都可以保留显微图像的局部细节特征;另一方面,笔者采用了积分图像的思想,提高了计算速度,可满足实时融合的应用场景。对于图像融合,都需要先进行图像配准,误配准将会严重影响融合结果,所以在后续工作中将继续研究相关配准算法以保证配准的准确性。此外,在显微镜的应用场景下,序列图像之间存在着强烈的相关性,充分利用好这部分相关信息可以提高融合算法的效果,这也是未来可以研究的课题。

