Gorenstein FCn-投射模
张文汇,高华云
(西北师范大学 数学与统计学院,甘肃 兰州 730070)
0 引言
文中提到的环均指有单位元的结合环,模均指酉模.20世纪90年代,Enochs等[1-2]引入了Gorenstein投射模(Gorenstein内射模, Gorenstein平坦模)及模的Gorenstein投射维数(Gorenstein内射维数, Gorenstein平坦维数),这是Gorenstein同调理论的核心.近年来,Gorenstein同调代数的研究已经取得了很多重要成果,研究范围也从模范畴扩充到Abel范畴(例如模的复形范畴)以及非Abel范畴(例如三角范畴, E-三角范畴等).2012年,Gao等[3]引入了Gorenstein FP-内射模.称左R-模M是Gorenstein FP-内射模,如果存在FP-内射左R-模的正合列
E: …→E1→E0→E0→E1→…,

P: …→P1→P0→P0→P1→…,
使得M≅Ker(P0→P1),并且对任意内射维数有限的有限余表示右R-模Q,序列HomR(P,Q)正合.受以上文献的启发,本文引入FCn-投射模和Gorenstein FCn-投射模,并讨论这两类模的同调性质.
以下除非特别说明,模均指左R-模.我们用id(M)表示R-模M的内射维数,P(R)表示所有投射R-模构成的类,N表示自然数集,Z表示整数集.文中没有介绍的符号和术语请参考文献[6].
设n是一非负整数.称R-模M是有限n-余表示模[7],如果存在R-模的正合列
0→M→E0→…→En-1→En,
其中Ei(i=0,1,2,…,n)是有限余生成内射模;称上述正合序列为模M的有限n-余表示.记FCn为有限n-余表示模类.特别地,FC0是有限余生成模类,FC1是有限余表示模类.称环R是左n-余凝聚环[7],如果任意有限n-余表示左R模是有限(n+1)-余表示的.特别地,左0-余凝聚环就是余Notherian环[8];左1-余凝聚环就是余凝聚环.称R-模类X是投射可解类[9],如果P(R)⊆X,并且在任意短正合序列0→A→B→C→0中,若C∈X,则A∈X当且仅当B∈X.
1 FCn-投射模
作为FC-投射模的推广,我们引入FCn-投射模,并在左n-余凝聚环上讨论这类模的同调性质.以下总假定n是正整数.

特别地,FC1-投射模就是FC-投射模.
注1由定义1可知,投射模和FC-投射模都是FCn-投射模;FCn-投射模关于扩张、直和及直和项都封闭.
引理1设R是左n-余凝聚环,则以下结论成立:
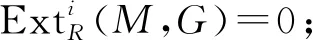
(2)在R-模的任意短正合序列
0→A→B→C→0


0→G→E0→…→En-1→En→…,
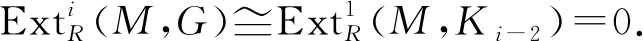
(2)对任意有限n-余表示模G,由长正合列引理可知存在正合列

推论1设R是左n-余凝聚环,则FCn-投射模类是投射可解类.
2 Gorenstein FCn-投射模
定义2称R-模M是Gorenstein FCn-投射模,如果存在FCn-投射模的正合列
P:…→P-2→P-1→P0→P1→…,
使得M≅Ker(P0→P1),并且对任意内射维数有限的有限n-余表示模G,序列HomR(P,G)正合.
注2( i )由对称性,若M是Gorenstein FCn-投射模,则序列P中各同态的像、核和余核都是Gorenstein FCn-投射模;
( ii )投射模、FC-投射模、FCn-投射模都是Gorenstein FCn-投射模;
例1任意Gorenstein投射模是Gorenstein FCn-投射模.
证明若M是Gorenstein投射模,则存在投射模的正合列
P: …→P-2→P-1→P0→P1→…,
并且M≅Ker(P0→P1).因此只需证对任意内射维数有限的有限n-余表示模G,序列HomR(P,G)正合,但这由模G的内射维数有限可得.故M是Gorenstein FCn-投射模. 】
命题1设R是左n-余凝聚环,M是R-模,则M是Gorenstein FCn-投射模当且仅当以下条件成立:
(1)存在FCn-投射模的正合列
P: …→P-2→P-1→P0→P1→…,
使得M≅Ker(P0→P1);
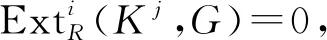
证明必要性.设M是Gorenstein FCn-投射模,则存在R-模的正合列
P: …→P-2→P-1→P0→P1→…,


定理1设R是左n-余凝聚环,M是R-模,则M是Gorenstein FCn-投射模当且仅当存在FCn-投射模的正合列
P: …→P-2→P-1→P0→P1→…,
使得M≅Ker(P0→P1).
证明只需证明充分性.由定义2只需证明对任意内射维数有限的有限n-余表示模G,序列HomR(P,G)正合.设id(G)=m<∞,我们对m进行数学归纳.
当m=0时,结论自然成立.
现设m≥1,由R是左n-余凝聚环知G∈FC∞,故存在正合列0→G→N→L→0,其中N是有限余生成内射模,L是有限n-余表示模并且id(L)≤m-1.在复形的短正合列
中,序列HomR(P,N)正合,且由归纳假设知序列HomR(P,L)正合,所以由文献[10]定理6.3知,序列HomR(P,G)正合,故M是Gorenstein FCn-投射模. 】
推论2设R是左n-余凝聚环,M是R-模,则以下结论等价:
(1)M是Gorenstein FCn-投射模;
(2)存在FCn-投射模的正合列
P: …→P-2→P-1→P0→P1→…,
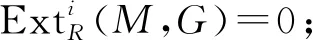
(3)存在R-模的正合0→M→P→K→0,其中P是FCn-投射模,K是Gorenstein FCn-投射模;
(4)存在R-模的正合列
0→M→P0→P1→…,
其Pj(j∈N)是FCn-投射模.
证明(1)⇒(2),(1)⇒(3)⇒(4)易见.
(4)⇒(1).设…→P-2→P-1→M→0是M的投射分解,与(4)中正合列首尾相接可得正合列…→P-2→P-1→P0→P1→…,其中Pj(j∈Z)是FCn-投射模,且M≅Ker(P0→P1).由定理1可知M是Gorenstein FCn-投射模. 】
命题2设R是左n-余凝聚环,0→M→N→L→0是R-模的正合列,则以下结论成立:
(1)若N是FCn-投射模,L是Gorenstein FCn-投射模,则M是Gorenstein FCn-投射模;
(2)若L是FCn-投射模,M是Gorenstein FCn-投射模,则N是Gorenstein FCn-投射模.
证明(1)由推论2可得.
(2)由M是Gorenstein FCn-投射模知,存在正合列0→M→P→K→0,其中P是FCn-投射模,K是Gorenstein FCn-投射模.考虑推出图

其中P,L是FCn-投射模,故Q是FCn-投射模.利用中间列由(1)可知,N是Gorenstein FCn-投射模. 】
定义3称环R是左GFCnP-闭环,如果Gorenstein FCn-投射左R-模类关于扩张封闭.
定理2设R是左n-余凝聚环,则R是左GFCnP-闭环当且仅当Gorenstein FCn-投射模类是投射可解类.
证明充分性易见.
必要性.设R是左GFCnP-闭环,只需证明在R-模的任意正合列0→M→N→L→0中,若N,L是Gorenstein FCn-投射模,则M是Gorenstein FCn-投射模.
因为N是Gorenstein FCn-投射模,所以存在R-模的正合列0→N→F→Q→0,其中F是FCn-投射模,Q是Gorenstein FCn-投射模.考虑推出图

因为L和Q都是Gorenstein FCn-投射模且R是左GFCnP-闭环,所以E是Gorenstein FCn-投射模.对中间行应用推论2可知,M是Gorenstein FCn-投射模. 】
由定理2和文献[2]命题1.4易得如下推论.
推论3设R是左n-余凝聚的左GFCnP-闭环,则Gorenstein FCn-投射模类关于直和项封闭.
以下讨论FCn-投射模、Gorenstein FCn-投射模和其他模类间的关系.
定理3设R是左n-余凝聚环,且任意有限n-余表示R-模的内射维数有限,则以下结论等价:
(1)任意R-模是Gorenstein FCn-投射模;
(2)任意内射R-模是FCn-投射模;
(3)任意Gorenstein内射R-模是Gorenstein FCn-投射模;
(4)任意内射R模是Gorenstein FCn-投射模;
(5)任意有限生成R-模是Gorenstein FCn-投射模;
(6)任意循环R-模是Gorenstein FCn-投射模;
(7)任意有限n-余表示R-模是内射模;
(8)任意R-模是FCn-投射模.
证明(1)⇒(3)⇒(4),(8)⇒(1)⇒(5)⇒(6)易见.
(4)⇒(2).任取内射模E,由(4)知E是Gorenstein FCn-投射模,故存在可裂的短正合列
0→E→P→L→0,
其中P是FCn-投射模,L是Gorenstein FCn-投射模.因为FCn-投射模类关于直和项封闭,所以E是FCn-投射模.
(2)⇒(1).对任意R-模M,设其投射分解和内射分解分别为
首尾相接可得正合列
P: …→P1→P0→E0→E1→…,
其中Pj(j∈N)是投射模,Ei(i∈N)是内射模,且M≅Im(P0→E0).由条件(2)知,Ei(i∈N)是FCn-投射模,故序列P是FCn-投射模的正合列.由定理1即知M是Gorenstein FCn-投射模.


3 Gorenstein FCn-投射维数
定义4定义R-模M的Gorenstein FCn-投射维数GFCn-pd(RM)为:GFCn-pd(RM)=inf{m∈N|存在正合列0→Qm→Qm-1→…→Q0→M→0,其中Qi(i=0,1,2,…,m)是Gorenstein FCn-投射模}.若上述集合为空,则规定GFCn-pd(RM)=∞.
注意到,投射模是Gorenstein FCn-投射模,于是由注记2(iii)和推论3易得如下结论.
引理2设R是左n-余凝聚的左GFCnP-闭环,M是R-模,考虑R-模的正合列
其中Qi,Pi(i=0,1,2,…,m-1)是Gorenstein FCn-投射模,则K是Gorenstein FCn-投射模当且仅当K′是Gorenstein FCn-投射模.
定理4设m是一非负整数,R是左n-余凝聚的左GFCn-P闭环,则以下结论等价:
(1)GFCn-pd(RM)≤m;
(2)存在R-模的正合列
0→Qm→Qm-1→…→Q0→M→0,
其中Qi(i=0,1,2,…,m)是Gorenstein FCn-投射模;
(3)在R-模的任意正合列
0→K→Qm-1→…→Q0→M→0
中,若Qi(i=0,1,2,…,m-1)是Gorenstein FCn-投射模,则K是Gorenstein FCn-投射模.
证明(1)⇒(2).设GFCn-pd(RM)=t≤m,则存在R-模的正合列
0→Qt→Qt-1→…→Q0→M→0,
其中Qi(i=0,1,2,…,t)是Gorenstein FCn-投射模.由于Qt是Gorenstein FCn-投射模,故存在正合列
0→Km→Pm-1→…→Pt→Qt→0,
其中Pm-1,…,Pt是FCn-投射模.因为Gorenstein FCn-投射模类是投射可解类,故Km是Gorenstein FCn-投射模,将上述两序列首尾相接即可得所需正合列.
(2)⇒(3),(3)⇒(1)由引理2及定义5即得. 】
命题3设R是左n-余凝聚环,在R-模的任意正合列0→N→Q→M→0中,若Q是Gorenstein FCn-投射模,则GFCn-pd(RM)≤GFCn-pd(RN)+1.进而,当R是GFCnP-闭环时,等号成立.
证明当GFCn-pd(RN)=∞时,结论自然成立.现设GFCn-pd(RN)=m<∞,则存在R-模的正合列0→Qm→…→Q0→N→0,其中Qi(i=0,1,2,…,m)是Gorenstein FCn-投射模.因此有正合列
0→Qm→…→Q0→Q→M→0,
其中Q,Qi(i=0,1,2,…,m)是Gorenstein FCn-投射模.故
GFCn-pd(RM)≤m+1=GFCn-pd(RN)+1.
进一步,若R是GFCn-P-闭环,要使等号成立只需证明GFCn-pd(RN)≤GFCn-pd(RM)-1.当GFCn-pd(RM)=∞时,结论自然成立.现设GFCn-pd(RM)=m<∞,且
0→K→Pm-2→…→P0→N→0
是模N的部分FCn-投射分解.将此正合列与已知短正合列首尾相接可得正合列
0→K→Pm-2→…→P0→Q→N→0,
其中Q,Pi(i=0,1,2,…,m-2)是Gorenstein FCn-投射模.由定理4可知K是Gorenstein FCn-投射模,因此GFCn-pd(RN)≤m-1. 】

