考虑损伤和不均匀冻胀的寒区隧道弹塑性统一解
蒋望涛 姜海强 马勤国† 李永东 李治国
(1.华南理工大学 土木与交通学院/亚热带建筑科学国家重点实验室/华南岩土工程研究院,广东 广州 510640;2.中铁隧道勘察设计研究院有限公司,广东 广州 511400)
寒区隧道开挖后含水围岩在低温环境中会冻结膨胀,冻结围岩边界受到衬砌及未冻结围岩的约束而产生冻胀力,隧道开挖与围岩冻胀会造成围岩冻胀损伤并导致围岩应力重分布,进而演变形成不同的应力区,增大寒区隧道结构与围岩的变形,严重影响寒区隧道的稳定性[1- 5]。因此,开展寒区隧道弹塑性解答的研究对于寒区隧道的稳定性具有重要意义,而围岩冻胀损伤及冻胀特性是计算寒区隧道围岩弹塑性解的重要基础。
目前考虑损伤的隧洞弹塑性解在矿井、地下巷道等得到了广泛应用[6- 9],但在寒区隧道中研究较少。代表性研究成果有:刘红岩等[10- 11]考虑岩体冻融循环损伤和弹性本构得到寒区隧道围岩冻胀力的理论计算方法;谭贤君等[12]基于热动力学、连续介质力学以及分凝势理论建立了围岩温度-渗流-应力-损伤(THMD)多场耦合模型,并开发相关数值计算程序求得多场耦合条件下的寒区隧道围岩冻胀力。寒区隧道围岩的冻胀特性是弹塑性求解的另一重要因素,而已有研究基于均匀冻胀特性,结合M-C准则、D-P准则以及粘弹性理论得到寒区隧道应力、应变以及位移的解析式[3- 4,13- 14]。然而寒区隧道由于冷空气流入沿着围岩径向方向表现为单向冻结状态,夏才初等[15]利用对比试验验证了饱和岩石在单向冻结条件下具有不均匀冻胀性,且不均匀冻胀性表现为横观各向同性冻胀;Lv等[16]推导了考虑横观各向同性冻胀的寒区隧道围岩M-C弹塑性解;Feng等[17]基于横观各向同性特性推导出5类D-P准则下的寒区隧道围岩弹塑性解。因此,寒区隧道围岩不仅有冻胀损伤特征,也有不均匀冻胀的特点,但鲜见文献将三者结合起来进行相关理论研究。
此外,已有寒区隧道围岩的弹塑性解大部分基于Mohr-Coulomb(M-C)和Druck-Prager(D-P)准则而建立,无法详细描述中间主应力对冻结围岩强度的发挥效果,所得结果偏向保守或偏向危险。统一强度理论在考虑中间主应力效应的基础上,通过调节中间主应力效应反映岩土类各种强度准则[18],具有很好的工程应用性。代表性的研究有:张常光等[19]考虑横观各向同性冻胀建立了寒区隧道位移及应力的塑性统一解;曾开华等[20]考虑中间主应力效应和围岩剪胀特性建立了深埋圆形隧道弹塑性统一解;张长安[21]基于统一强度理论对比分析了M-C准则、广义M-N准则及外接圆D-P准则的强度效应。
因此,本研究基于损伤理论推导出考虑损伤的寒区隧道统一强度理论,建立了弹塑性损伤力学计算模型,考虑中间主应力效应及不均匀冻胀特性求解得到寒区隧道弹塑性应力场和位移场的统一解;其次,探讨围岩损伤特征、不均匀冻胀特征以及中间主应力效应条件下的围岩应力场及位移场的分布规律;最后,分析各影响因素条件下寒区隧道衬砌上径向应力及塑性半径的变化趋势。本研究成果可为寒区隧道工程设计提供理论参考。
1 基本假设
基于损伤理论和统一强度理论,考虑寒区隧道围岩不均匀冻胀特性影响,求得寒区隧道应力与位移弹塑性统一解,并做出如下基本假设:
(1)衬砌视为弹性介质,围岩视为满足统一强度理论的弹塑性介质。
(2)隧道纵向长度远大于隧道横断面尺寸,故将隧道视为平面应变问题。
(3)隧道处于静水压力作用下,忽略衬砌和围岩重力的影响。
(4)将围岩视为不均匀冻胀介质,围岩不均匀冻胀系数保持常数不变,隧道纵向的线冻胀率和垂直方向的线冻胀率不相等,即为横观各向同性冻胀,但是在冻结过程中各自保持不变。
2 寒区隧道弹塑性损伤力学模型
寒区隧道弹塑性损伤力学计算模型如图1所示,计算模型包括4个区域:衬砌结构(Ⅰ区,rL>r≥ra,r为隧道径向半径),冻结塑性损伤区(Ⅱ区,rp>r≥rL),冻结弹性区(Ⅲ区,rf>r≥rp),未冻结弹性区(Ⅳ区,r≥rf)。冻结塑性损伤区(Ⅱ区)和冻结弹性区(Ⅲ区)围岩在低温环境下发生冻结膨胀,分别受到衬砌(Ⅰ区)和未冻结弹性区(Ⅳ区)的约束作用,产生冻胀反力作用在衬砌和未冻结弹性区上。
从图1得知:ra为隧道衬砌内半径;rL为隧道衬砌外半径;rp为冻结塑性损伤区半径;rf为冻结弹性区半径;σf为作用在衬砌与冻结塑性损伤区交界处的径向应力;σp为作用在冻结塑性损伤区与冻结弹性区交界处的径向应力;σh为作用在冻结弹性区与未冻结弹性围岩交界处的径向应力;p0为初始地应力。

图1 寒区隧道弹塑性损伤力学计算模型Fig.1 Elasto-plastic damage mechanics calculation model of cold regions tunnel图1中计算模型的各区域满足变形几何条件:
(1)
式中,εr和εθ分别为径向应变和切向应变,u为隧道径向位移,r为隧道径向半径。
基于不均匀冻胀特性和弹性理论,冻结围岩本构方程可表示为[14,16- 17]:
(2)
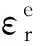
隧道径向的线冻胀率ξr和环向的线冻胀率ξθ满足下式关系[16,22]:
(3)
式中,k为不均匀冻胀系数,k>1代表着围岩的不均匀冻胀性,ξV为围岩体积冻胀率。
3 寒区隧道弹塑性统一解
如图1所示为弹塑性损伤力学计算模型,模型中有3个交界面,交界面处满足位移及应力连续边界方程,得到6个连续边界方程如下:
(4)

3.1 考虑损伤的统一强度理论
平面应变状态下最大和最小的主应力分别为σθ和σr,中间主应力为σz,满足σ1=σθ,σ2=σz,σ3=σr,统一强度理论[18- 20]如下:
σθ=Mσr+N
(5)
(6)
式中:M和N为统一强度方程参数;c为围岩黏聚力;φ为围岩内摩擦角;b为统一强度理论参数,取值范围为0~1,当b=0时,式(5)表示为M-C准则;当b=1时,式(5)退化为双剪应力准则;当1>b>0时,式(5)代表系列新强度准则。
基本假设条件(4)中假定围岩为横观各向同性介质,围岩损伤采用有效应力表示:
(7)

将式(7)代入式(5),统一强度理论可表示为
σθ=Mσr+(1-D)N
(8)
围岩单向压缩条件下的岩石应力应变曲线可表示为双线性[6- 9],如图2所示。图中:AB段为弹性阶段,弹性模量为E;B点为峰值强度点;BC段为塑性损伤软化阶段,降模量为λ。为了描述超过峰值后的损伤程度,定义损伤程度比值λ/Ef。
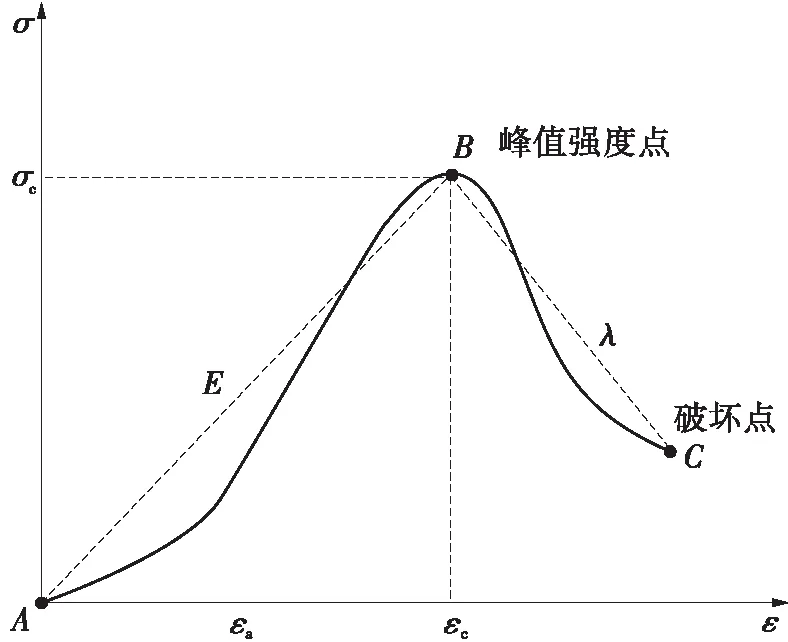
图2 岩石单轴压缩应力-应变曲线Fig.2 Stress-strain curve of rock under uniaxial compression
因此,围岩三维损伤演化方程为[6- 9]:
(9)
式中,εc为峰值应变,εi为等效应变。
等效应变εi可由ε1、ε2、ε3三向主应变表示:
(10)
考虑围岩剪胀特性,由已有研究成果[7]得知塑性损伤区内有效应变εi表达式:
(11)

将式(11)代入式(9)求得围岩三维损伤演化方程:
(12)
将式(12)代入式(8)求得考虑损伤的统一强度方程为
(13)
3.2 衬砌支护区
寒区隧道衬砌支护区视为厚壁圆筒弹性介质,衬砌仅受σf外压作用,利用弹性理论[23],求得应力如下:
(14)

衬砌支护结构弹性本构方程[23]为:
(15)

结合几何方程(1)得到衬砌支护区的径向位移表达式:
(16)
3.3 冻结塑性损伤区
平面应力应变状态下,冻结围岩塑性损伤区微分平衡方程为[23]:
(17)
将式(13)代入式(17),利用边界条件:当r=rL时,σr=σf,得到冻结围岩塑性损伤区应力表达式:
(18)
冻结塑性损伤区围岩应变包括塑性应变和弹性应变,由式(2)得到如下表达式:
(19)

在冻结塑性损伤区内,围岩应变分量满足协调方程:
(20)
将式(19)代入式(20),得到式(21):
(21)
由线性非相关流动性法则[24],得围岩塑性损伤区内塑性切向应变与径向应变之间满足以下关系:
(22)
根据式(22)线性非相关流动法则,结合式(21),得到
(23)
将式(18)代入式(2)得到冻结围岩塑性损伤区弹性应变分量表达式:
(24)
将式(24)代入式(23)得到冻结围岩塑性损伤区切向应变如下:
(25)


(26)
将式(26)代入式(25)得到冻结围岩塑性损伤区塑性切向应变表达式为
(27)
将式(24)和(27)代入式(1),以此得到冻结围岩塑性损伤区径向位移表达式为:

(28)
3.4 冻结弹性区
采用弹性力学理论[23]求得冻结围岩弹性区应力表达式:
(29)

将式(29)代入式(2)得到冻结围岩弹性区应变为:
(30)

利用式(30)和几何方程(1),得到冻结围岩弹性区径向位移:

(31)
3.5 未冻结弹性区
将未冻结围岩区视为厚壁圆筒弹性介质,利用弹性理论[23],求得应力为:
(32)

未冻结围岩弹性本构方程[23]表示为:
(33)

同理,相应的径向位移为
(34)
3.6 求解步骤
为了求解σf、σp、σh以及rp4个未知量,根据力学计算模型中6个边界条件,采用以下求解步骤:

(2)在r=rL、r=rp及r=rf交界处,式(4)中剩余4个边界条件,可化简表示包含4个方程的方程组。
(3)利用MATLAB软件对步骤(2)中的方程组进行求解,求出σf、σp、σh以及rp4个未知量的值。
4 算例分析
4.1 统一解验证
基于损伤理论和统一强度理论,考虑围岩不均匀冻胀特性建立寒区隧道弹塑性统一解。所得的弹塑性统一解包含统一强度理论参数b、不均匀冻胀系数k和围岩体积冻胀率ξV、损伤降模量λ以及位移释放系数η等因素的共同影响。隧道相关计算参数见表1。

表1 寒区隧道几何和材料特性表[14,17]1)Table 1 Geometrical and material properties of cold regions tunnel[14,17]
当b=0、k=1、λ=0以及η=0时,弹塑性统一解退化为文献[14]中考虑均匀冻胀的M-C准则统一解,将本研究推导的应力弹塑性统一解与文献[14]的应力解进行对比,如图3所示。
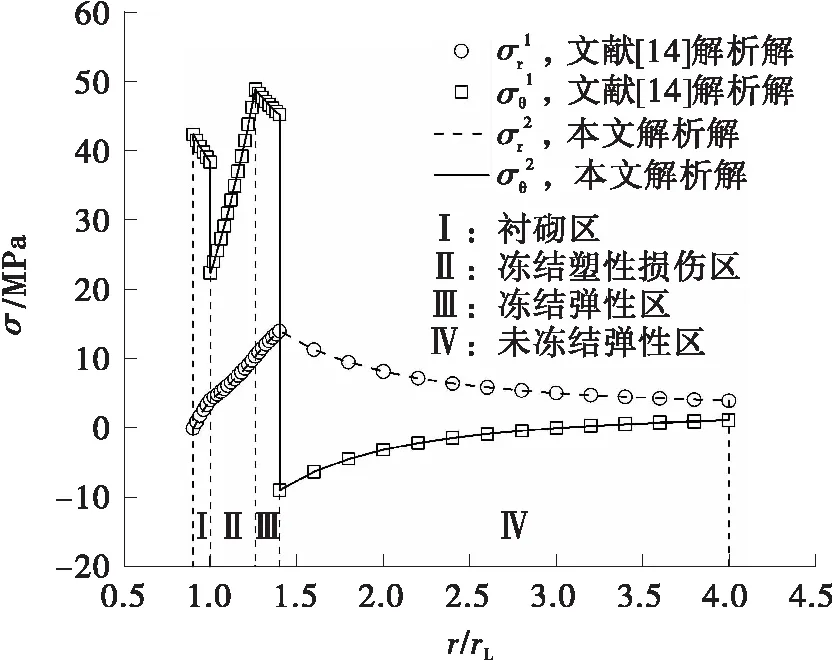
图3 本文解析解与文献[14]解析解的对比Fig.3 Comparison between results from this study and those of the reference[14]
从图3可以看出,当参数b=0、k=1、λ=0以及η=0时,本研究推导的应力弹塑性统一解与文献[14]的应力解完全吻合,验证了本研究推导的考虑损伤的寒区隧道弹塑性统一解的正确性。
4.2 围岩应力场及位移场分析
为分析寒区隧道应力场及位移场的分布规律,考虑损伤降模量λ、围岩体积冻胀率ξV、不均匀冻胀系数k以及统一强度理论参数b等4个因素的影响,得到不同影响因素条件下的寒区隧道应力及位移分布曲线。
4.2.1 围岩损伤特征
图4示出了不同损伤程度下寒区隧道应力分布及弹塑性区位移分布曲线。随着λ/Ef的增大,支护区环向及径向应力以及冻结弹性区的切向应力逐渐增大,而冻结塑性损伤区的切向应力及冻结区的径向应力却不断减少,其余区域内的应力变化较小。随着λ/Ef比值增大,相同距离处的位移不断增大,λ/Ef比值从0.0增至1.5时塑性区域外壁面的位移保持不变,但塑性半径向外扩大了0.221 m,塑性区域内壁面位移增大了0.948 mm,且冻结塑性区内零位移半径增大0.090 m。这表明损伤程度变大不仅能增大寒区隧道衬砌及围岩变形,也能扩大冻结围岩塑性区半径,在寒区隧道工程设计中需要考虑围岩冻结损伤程度,提高衬砌支护及时性和采取保温防冻措施能有效减小围岩损伤程度。

(a)应力分布曲线

(b)弹塑性区位移分布曲线图4 损伤程度对应力和位移的影响(k=2,b=0.5,ξV=0.016 5)Fig.4 Influence of damage degree on stress and displacement(k=2,b=0.5,ξV=0.016 5)
4.2.2 围岩不均匀冻胀特性
图5示出了不同体积冻胀率下寒区隧道应力分布及弹塑性区位移分布曲线。围岩体积冻胀率的增加会显著提高寒区隧道围岩各区域的应力,对隧道衬砌及围岩的安全十分不利。当ξV从0.010 5增大至0.022 5时,冻结塑性区内、外壁面位移分别相对增大了128.36%和172.07%,塑性区域半径增大了0.138 m,但塑性区内位移零点保持不变。这表明在寒区隧道工程中需要详细考虑冻胀作用,通过采取保温防冻措施提高寒区隧道的抗冻性能。

(a)应力分布曲线

(b)弹塑性区位移分布曲线图5 体积冻胀率对应力和位移的影响(λ/Ef=0.5,k=2,b=0.5)Fig.5 Influence of frost heave ratio of volume on stress and displacement(λ/Ef=0.5,k=2,b=0.5)
图6示出了不同不均匀冻胀系数时的寒区隧道应力分布及弹塑性区位移分布曲线。可以看出,随着参数k从1增大至3,作用于衬砌上的冻胀力增大了0.16 MPa,冻结弹性区的切向应力得到有效减缓,其余区域应力变化不大。同时,不均匀冻胀系数k的增大将塑性区域半径缩小了0.25 m,其余位置处位移曲线较接近。这说明考虑不均匀冻胀系数相比均匀冻胀系数对于寒区隧道设计更有利,且围岩不均匀冻胀系数需要通过试验测试得到。

(a)应力分布曲线
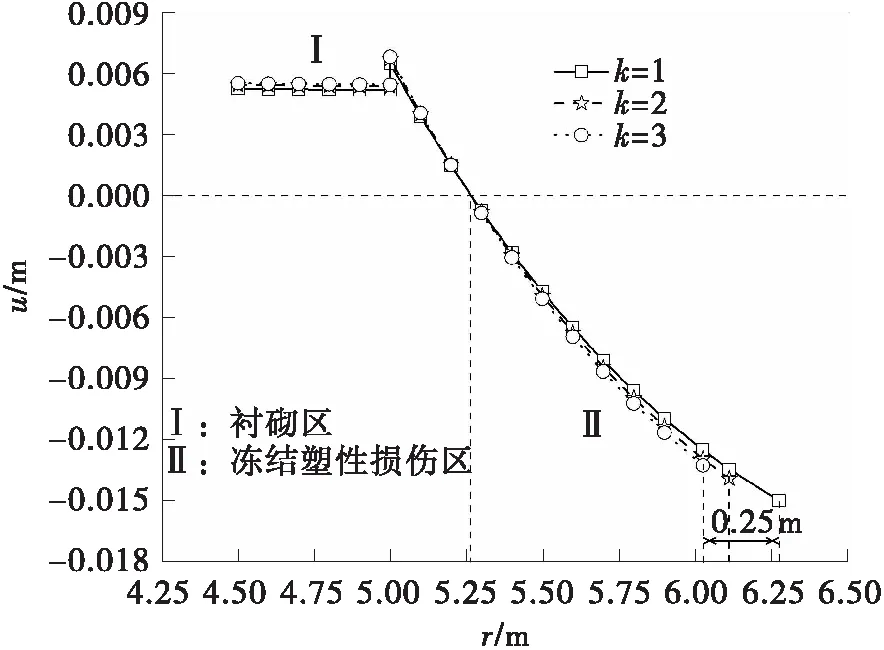
(b)弹塑性区位移分布曲线图6 不均匀冻胀系数对应力和位移的影响(λ/Ef=0.5,b=0.5,ξV=0.016 5)Fig.6 Influence of coefficients of non-uniform frost heave on stress and displacement(λ/Ef=0.5,b=0.5,ξV=0.016 5)
4.2.3 中间主应力效应
图7示出了不同统一强度理论参数b下的寒区隧道应力分布及弹塑性区位移分布曲线。随着参数b从0.0增加到1.0,衬砌区及冻结塑性损伤区的环向应力不断减少,其余区域应力差距不大。这表明考虑中间主应力效应能有效发挥冻结围岩的承载潜能。同时,随着参数b的增大,冻结塑性损伤区内同一位置处的位移逐渐减少,塑性区域内、外壁位移分别相对减少了42.88%和17.78%,塑性区域半径缩小了0.278 m,且塑性区域内零位移半径减小了0.090 m。这说明考虑中间主应力系数能有效缩小寒区隧道的位移及塑性半径,在寒区隧道工程设计时不容忽视。

(a)应力分布曲线

(b)弹塑性区位移分布曲线图7 统一强度理论参数对应力和位移的影响(λ/Ef=0.5,k=2,ξV=0.016 5)Fig.7 Influence of parameter of unified strength theory on stress and displacement(λ/Ef=0.5,k=2,ξV=0.016 5)
4.3 参数分析
从上文分析得知,影响寒区隧道的弹塑性解的因素包括损伤程度、不均匀冻胀特性以及中间主应力效应等。为更进一步分析本文推导出来的弹塑性统一解参数构成,详细分析下述参数对衬砌支护上的径向应力σf和塑性半径rP的影响,参数包括:损伤程度比值λ/Ef、体积冻胀率ξV、不均匀冻胀系数k、统一强度理论参数b、初始地应力p0以及位移释放系数η,如图8-13所示。

图8 不同λ/Ef的应力及塑性半径曲线Fig.8 Stress and plastic radius curves with different λ/Ef

图9 不同ξV的应力及塑性半径曲线Fig.9 Stress and plastic radius curves with different ξV

图10 不同k的应力及塑性半径曲线Fig.10 Stress and plastic radius curves with different k

图11 不同b的应力及塑性半径曲线Fig.11 Stress and plastic radius curves with different b
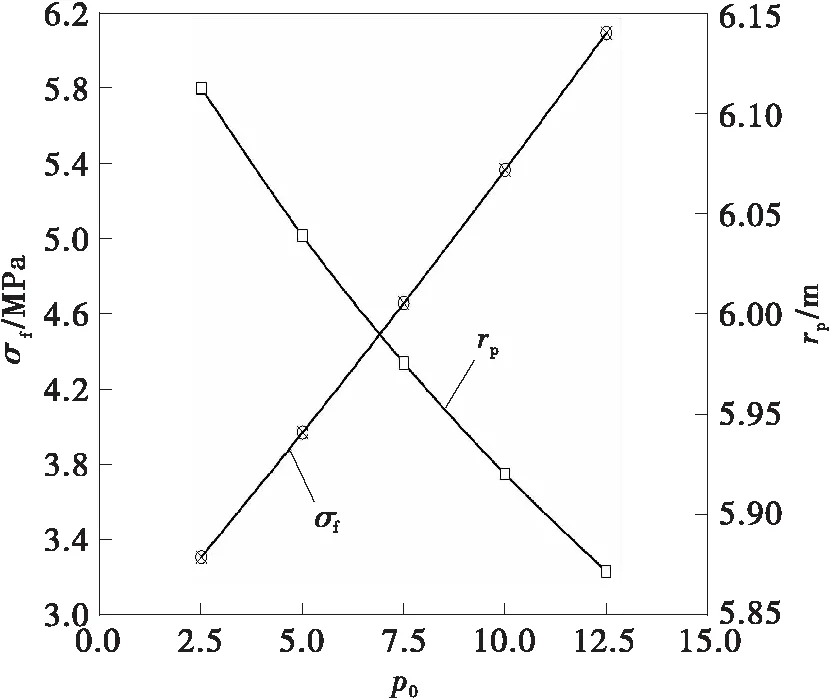
图12 不同p0的应力及塑性半径曲线Fig.12 Stress and plastic radius curves of different p0
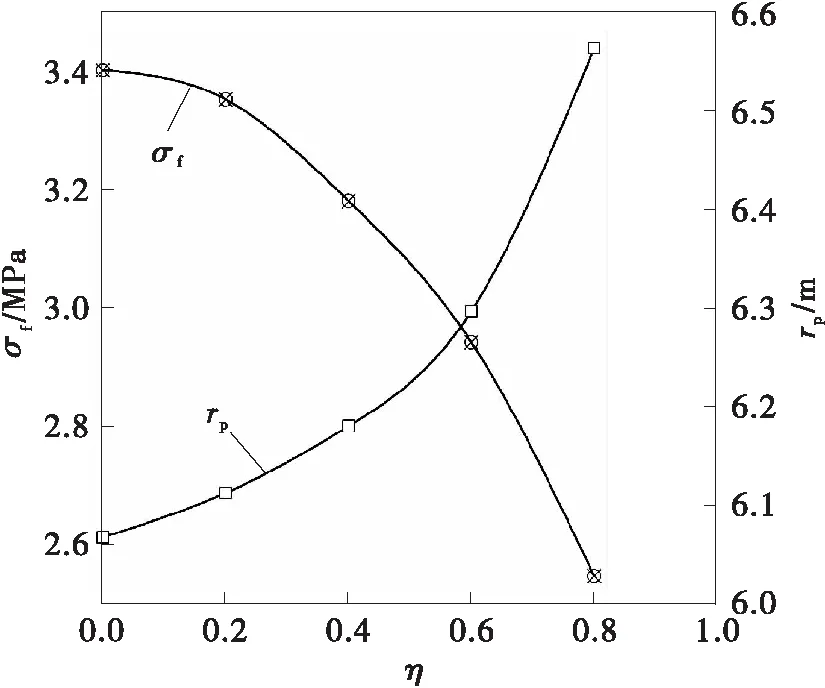
图13 不同η的应力及塑性半径曲线Fig.13 Stress and plastic radius curves of different η
图8示出了不同损伤程度比值λ/Ef的应力σf和塑性半径rp曲线,随着比值λ/Ef从0.00增大至2.00时,应力σf增大了0.904 MPa,相对增加28.10%,塑性半径从6.041 m变化至6.499 m,相对增加7.58%。这表明冻结塑性损伤区λ/Ef比值越大,围岩冻结塑性区半径越大,衬砌支护结构越不安全。
体积冻胀率ξV代表着寒区隧道围岩的冻结膨胀程度,如图9所示。当参数ξV从0.004 5增加到0.028 5时,应力σf从0.802 MPa增大至5.897 MPa,相对增加了6.353倍,塑性半径相对增加了0.489 m。这说明围岩体积冻胀率的增加对衬砌支护结构及围岩冻胀区域有着明显影响,当隧道内围岩具有较高的体积冻胀率时,隧道结构由于冻胀而引发的变形也会越大。
图10示出了不同不均匀冻胀系数k对应的应力σf和塑性半径rp曲线,当参数k从1.0变化至3.0时,应力σf相对增大了0.163 MPa,塑性半径却相对减小了0.250 m。这表明考虑均匀冻胀对于寒区隧道工程设计偏于危险,而考虑不均匀冻胀是十分有必要的。
图11示出了不同统一强度理论参数b对应的应力σf和塑性半径rp曲线,当参数b从0.0增加至1.0时,应力σf和塑性半径rp逐渐减小,其中应力σf相对减小了30.06%,塑性半径相对减小了0.273 m。进一步说明考虑中间主应力系数能有效发挥寒区隧道围岩的承载潜能。
图12示出了不同初始地应力p0对应下的应力σf和塑性半径rp曲线,随着p0从2.5 MPa增加至12.5 MPa,应力σf从3.303 MPa增大至6.093 MPa,相对增加了0.844倍,而塑性半径却相对减小了0.241 m。这说明初始地应力p0越大,寒区隧道需要更高强度的衬砌支护。
位移释放系数η代表着隧道开挖后支护的及时性。如图13所示,当参数η从0.0增加至0.8时,应力σf相对减小了25.12%,而塑性半径却相对增大了0.496 m。这表明η越大隧道开挖围岩初始变形增大,后期衬砌支护冻胀变形量变小,同时围岩冻结区更容易出现塑性损伤现象。
5 结论
(1)基于损伤理论模型,考虑中间主应力效应和寒区隧道围岩不均匀冻胀特性,建立了寒区隧道围岩弹塑性应力场和位移场的统一解。通过与相关文献寒区隧道M-C准则应力解对比分析,验证了本研究推导的统一解的正确性,结果可为寒区隧道工程设计提供理论参考,具有很好的应用性。
(2)塑性损伤特征、围岩不均匀冻胀特性以及中间主应力效应对寒区隧道的应力场和位移场有着显著的影响。不考虑围岩塑性损伤及冻胀特征对于寒区隧道是偏危险的,考虑不均匀冻胀特性更能代表寒区隧道围岩实际的冻胀特性,考虑中间主应力效应能有效发挥冻结围岩的承载潜能。由此可见,考虑寒区隧道围岩的损伤、冻胀特性及中间主应力效应是非常有必要的。
(3)寒区隧道衬砌支护上径向应力σf和塑性半径rp受很多因素影响,增大λ/Ef和ξV会加快塑性半径的变化,围岩更容易达到塑性状态;增大k和p0对衬砌支护不利,但冻结塑性区半径反而变小;增大b能发挥冻结围岩的承载潜能,有效缩减冻结塑性区半径;增大η意味支护拖延,围岩更容易转为塑性状态,围岩变形增大。

