基于Python使用模拟退火算法的气弹簧优化选项方案

陈鹏

江苏仅一联合智造有限公司，江苏镇江，212300

0 引言

在非标准设备的开发过程中，气弹簧经常使用在防护罩或防护门等的支撑场合。随着非标设备的发展越来越快，种类越来越多，防护罩或者防护门的外形也各不一样，如何快速的，合理准确地对气弹簧的性能和安装位置等快速选型设计就显得格外重要[1]。

本文利用Python软件，通过模拟退火算法优化了气弹簧选型的过程，通过计算可以得出最优的气弹簧力和安装位置，此方法在实际应用过程中能够快速选型完成，缩短了设计周期，提高了准确性。

1 理论基础

1.1 气弹簧的工作原理

普通气弹簧的原理如下图1所示，在气弹簧密闭的墙体内注入高压惰性气体，活塞左右两侧设有通孔，因活塞两侧表面积不同，因此在气体压力下，会推动活塞向图左侧移动，即产生气弹簧弹力F，弹力大小可以通过改变内腔气压大小或者活塞杆直径等予以设定[2]。如图1所示，F1，F2分别为无活塞杆和有活塞杆高压气体作用在活塞面上的压力；S1，S2为无活塞杆侧和活塞杆的截面积；因此气弹簧力的平衡方程为：

图1 普通气弹簧工作原理

气弹簧受力压缩时，活塞杆与内壁的摩擦力与图2气弹簧输出力曲线压力相反；释放伸长时，活塞杆与内壁的摩擦力与释放力相反虽然在受力压缩和释放伸长的两个过程的刚度（斜率）是相等的，但是在运动的起始和终止位置会存在力的跳跃，跳跃值为2倍的摩擦力所以气弹簧输出力曲线会呈现滞环现象，如图3所示。

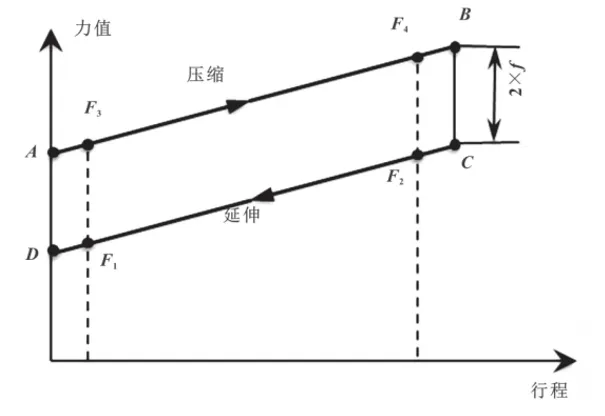
图2 气弹簧输出力曲线

图3 气弹簧设计简图

1.2 常规气弹簧设计流程

气弹簧支撑系统在非标设备的防护门或者防护罩上布置的主要方式就是翻转式[3-4]。无论防护罩和防护门的外形如何变化，其支撑的简化模型均为相同，遵循力矩平衡。张建国等[5]对尾门受力进行分 析并建立力矩平衡方程如式 (1),当尾门打开或关闭到 任意角度时,其重力、气弹簧支撑力、手臂操纵力对铰 链轴的力矩之和为零。

此时，门关闭和打开状态时：

非标设备防护罩的一般设计流程如下：

确定重力数值G，防护门关闭或打开状态下重心位置，根据公式（2），求出：

综上：

气弹簧力F为：

为保证防护门打开小角度时，气弹簧力能够尽可能支撑防护罩或者防护门重量，一般F取值为，或略小于。

定义：

我们称此时气弹簧可以“悬停”（不增加外力的情况下，防护门可以停在任意位置），即。

然而上述算法仅能计算出特定的机架固定点坐标以及防护门固定点坐标下，值大小，并不能减小值，若此时值非常大，则无法实现“悬停”。

反观上述，常规气弹簧设计存在着以下问题：①设计偏差较大，，和气弹簧最大力和最小力不存在绝对对应关系；②安装位置对于设计计算的影响很大；③设计时确定气弹簧的安装位置计算时间长，且无法确定最优解；④计算出的气弹簧在实际使用中与设计结果相差甚远。

2 Python的模拟退火算法优化设计

2.1 基于Python软件的编程

Python作为一种简单、易学、易读、易维护的开源的编程语言，拥有非常强大的面向对象的能力，同时也具备一定的可扩展性和可扩充性，丰富的第三方库也让用户可以进行web开发，爬虫，科学计算等。为了充分利用Pyhton软件的科学计算等的优势，使用Python编写了气弹簧优化设计的计算程序。

2.2 模拟退火算法

模拟退火算法(Simulated Annealing，SA)最早的思想是由N.Metropolis[6]等人于1953年提出。1983年，S.Kirkpatrick 等成功地将退火思想引入到组合优化领域。模拟退火算法从某一较高初温出发，伴随温度参数的不断下降,结合概率突跳特性在解空间中随机寻找目标函数的全局最优解，目前已在工程中应用非常广泛。

本文利用模拟退火算法来进行优化设计过程中数据的庞大计算量，模拟退火算法优化过程详见图4。

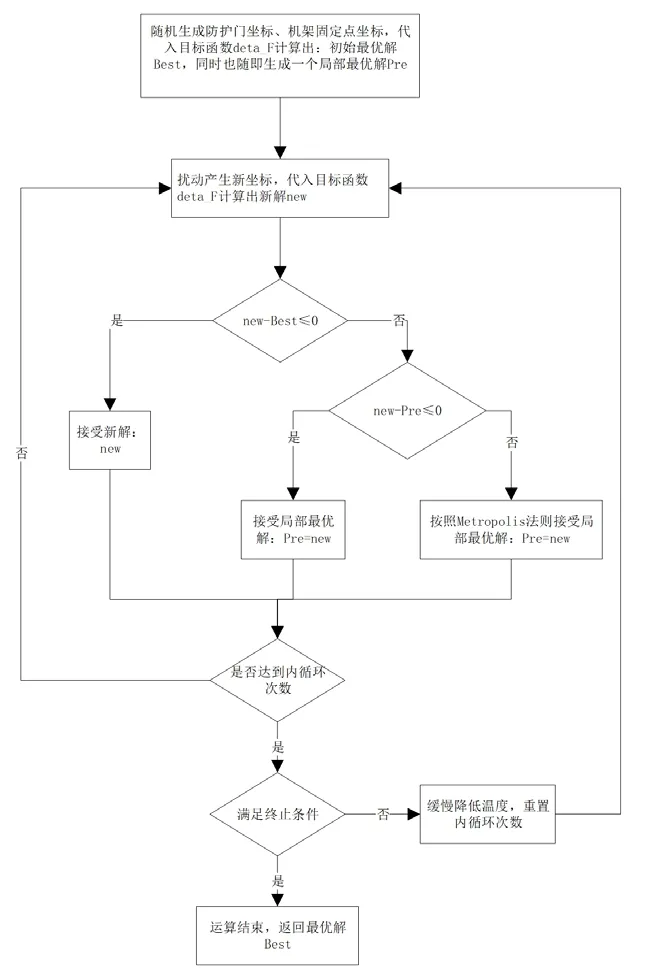
图4 模拟退火算法优化过程

2.3 确定基础模型与基础参数

利用inventor三维建模软件，在原始坐标（0,0,0）处创建模型，绘制防护门的基础模型，得到如下图5所示。

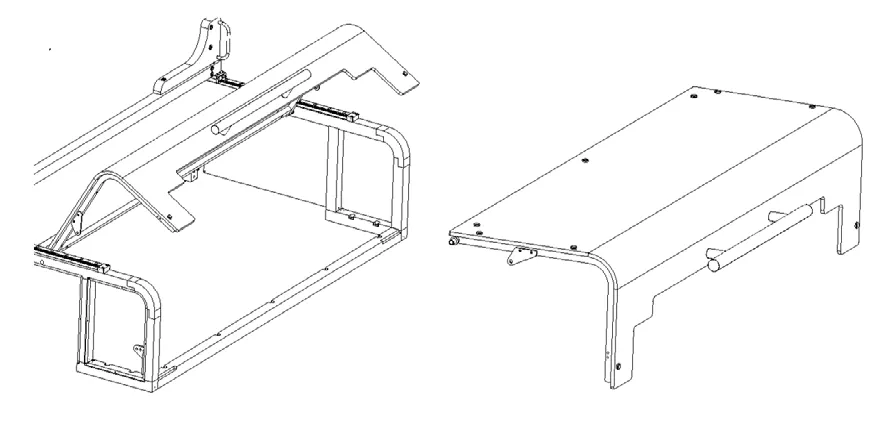
图5 防护门机架即防护门装配三维图

其中对气弹簧参数选型主要影响因素有旋转点的位置或者坐标，防护门固定点的位置或者坐标，机架固定点的位置或者坐标，防护门的质量和重心的位置或者坐标，气弹簧的预估数量共计6大设计参数，通过将旋转点置于（0,0）平面处，按照下图示意图创建坐标系，得出各设计参数位置坐标，见如下汇总表。

图7 坐标系划分示意图

2.4 选取变量

本文主要对气弹簧的两个安装位置或者坐标进行随机性遍历，即对机架固定点坐标和防护门固定点坐标，根据模型的外形尺寸，设定坐标随机性遍历的范围，如表2所示。

表2 变量汇总表

2.5 目标函数构造

根据公式（3），可得当防护门打开θ角度时，气弹簧的力计算如下：

其中G为重力，LGθ为防护门打开θ角度时，重力的力臂；Lfθ为防护门打开θ角度时，气弹簧的力臂，Fθ为防护门打开θ角度时，所需的气弹簧的力，此处暂不考虑气弹簧摩擦力，操作力矩等。

2.6 算法设计

2.6.1 参数初始化

表3 初始化参数

2.6.2 降温函数

降温函数的选择直接影响了算法的搜索速度，温度高时全局搜索，温度低时，算法进行局域搜索。本次采用标准降温函数[7-8]：

其中TK退火后的温度，T0为初始温度，为了获取更多的衰减次数，初始温度取10000℃，K为衰减系数，可在0.8～0.99之间选择，本文取0.99。

2.6.3 终止规则

模拟退火算法经常使用结束温度作为其终止规则，即当温度达到结束温度时退火过程终止，即。随着模拟退火算法的运行，退火温度呈指数下降。此时温度会无限接近于0，以本文温度衰减系数0.99，初始温度200为例，降低到本文T_end=0.001以下为止，需要迭代1604次[9]，再包含内部内循环次数，能达到百万级的计算量，足以获得靠近全局最优解的方案。另，为保证每次模拟退火算法得出结论数据能够横向比较，增加了对于最优解集合内数量的要求（本文设定最优解数量至少为12），因此终止规则如下：

3 应用实例

以本文表1内参数为例，按照图6模型进行汇总，可以计算出优化前气弹簧基础设计参数如下：

图6 防护门及机架固定点示意图

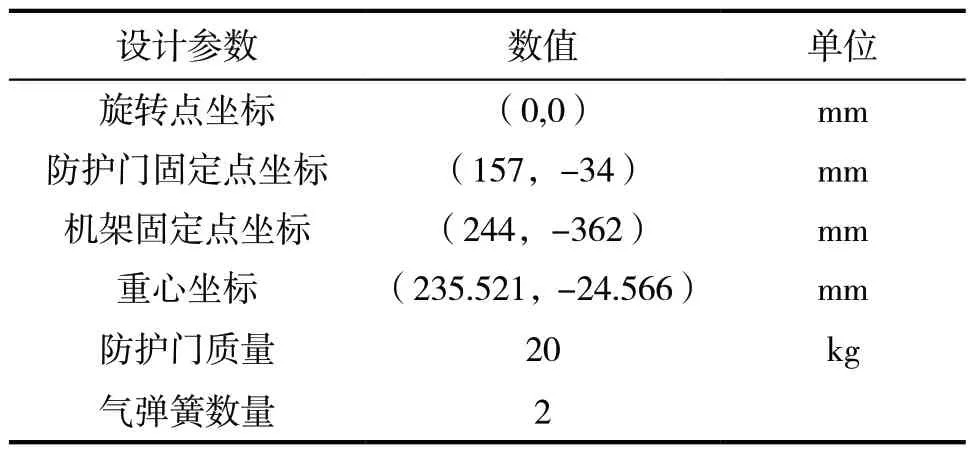
表1 设计参数汇总表

根据2.1节中图5所显示的模拟退火算法的优化设计计算流程，依据2.3节中变量汇总表内的最大值和最小值的取值范围，经过模拟退火算法，Python输出最优解列表trace内参数如图8所示。

图8 气弹簧力波动值ΔF

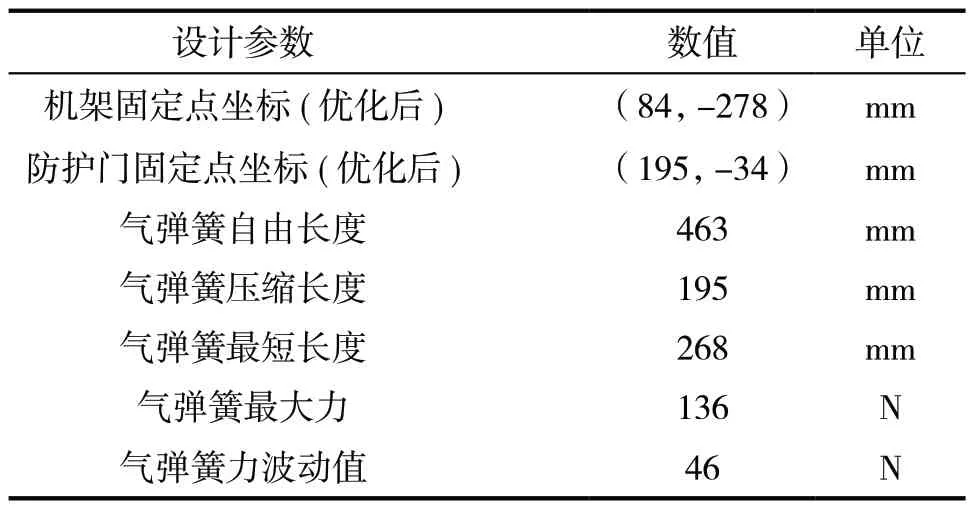
表5 优化设计后参数汇总表

优化前的计算结果和优化后的计算结果如表4第4行和表5第6行所示，气弹簧力波动值表明了防护门打开的稳定性，使用模拟退火算法计算后的结果要明显优于计算前的结果，气弹簧力波动值也从132降低到了46，降低了65%，而表5第6行即为整个防护门打开过程中气弹簧所需要的最大力，也是后续选型的参考值，同时也利用Python计算出了气弹簧的自由长度、压缩长度等关键选型参数，便于后续选型使用。

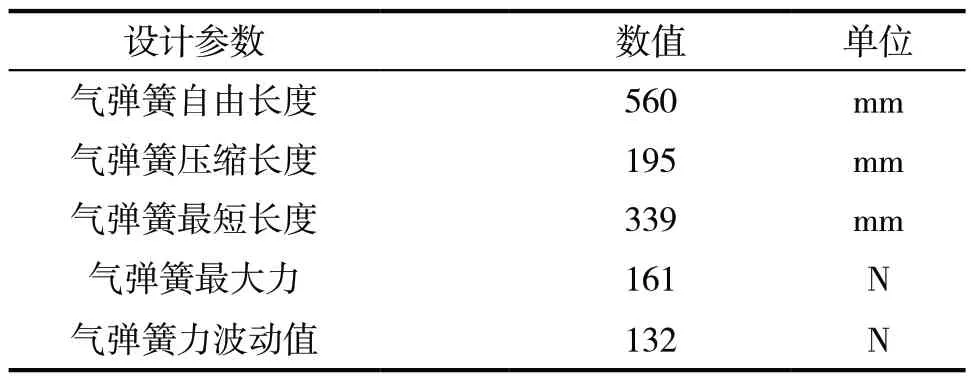
表4 优化前气弹簧参数表

将该结果用于最终设计，并测量了最终防护门的开关性能，并且在开关过程当中实现了上文所述的悬停。实测结果和优化计算结果有很好的吻合度。

4 结语

本文基于Python平台，利用模拟退火算法对气弹簧的两端固定点进行了优化设计，降低了气弹簧力波动值，从而提高了防护门开关的稳定性，减少了因设计者经验或能力所限造成的气弹簧选型错误的问题。并且本文提供的气弹簧选型的优化设计思路，有效解决了传统方法设计不准确、需要反复核准的问题，能够一次准确地找到最优的设计结果，与此同时Python同步计算出气弹簧选型所需要的关键参数，直接完成选型工作，为广大设计者提供了新的思路。