可调节活动式破风圈减振机制与效果分析

宋波，王蓉*，陈乃刚

(1.北京科技大学土木与资源工程学院，北京 100083；2.强震区轨道交通工程抗震研究北京市国际科技合作基地, 北京 100083；3.浪潮集团发展有限公司，济南 250014)

发电厂中采用的钢制脱硫塔属于典型的高耸薄壁结构[1]，其特点是塔体直径小、中部质量大，在风荷载作用下，上部烟囱段变形较大，对于此类结构来说极易发生损伤破坏，如国内深圳赛格大厦顶部桅杆发生风致涡激共振导致大厦有感振动，因此研究其风振响应及减轻措施具有很重要的现实意义与价值。

一般对于结构产生的风振效应，通常是在结构上安装调频减振装置来达到耗散能量、降低风振响应的效果，使用较广泛的是安装调谐质量阻尼器(tuned mass damper,TMD)，中外学者对此开展了大量研究。Minghini等[2]分析了烟囱可能发生局部破坏的原因；Dai等[3]用TMD来控制桥梁的涡激振动；Kwon等[4]验证了仿生调谐质量阻尼器在高层建筑风振控制中的有效性；陈政清等[5]、刘石等[6]将TMD应用于输电塔并进行了减振效果的风洞试验分析；刘春城等[7]将环形TMD应用于变电站高压电器设备的振动控制；汪权等[8]验证了建筑隔振和TMD混合振动方法可有效抑制结构风振作用；苏恩龙[9]提出了利用套环和肋条抑制化工塔风致振动的被动控制方法；李亚峰等[10]将TMD进行优化，研究了旋转惯致双调谐质量阻尼器的减振性能；鲁正等[11]将地震作用下调谐质量阻尼器与调谐型颗粒阻尼器的减振效果进行了试验对比并进行优化设计。

此外，还有学者通过在结构上设置破风圈的方式来减少风振效应。Huang等[12]在钢管上安装扰流板抑制输电塔钢管的涡振；朱志斌[13]提出了在钢烟囱顶部1/3位置处设置破风圈来避免发生共振。

为减小脱硫塔结构在风荷载作用下的振动效应，由实际工程中的平台楼梯得到启示，以此工程实际为背景，在上部烟囱段设计了一个可以进行调节活动的板，考虑流固耦合效应下并进行数值模拟计算，研究此结构对于风振效应是否具有减轻效果。

1 工程背景

在实际工程中，在钢烟囱上部会布置检修楼梯，其结构类似螺旋板型破风圈，如图1所示，受到此结构的启发，在自立式钢烟囱上部建立可调节的活动式破风圈，在风速的作用下，该结构会顺着风向而绕着铰接点转动，从而耗散风的能量，活动式破风圈示意图如图2所示。

图1 平台楼梯结构现场布置图

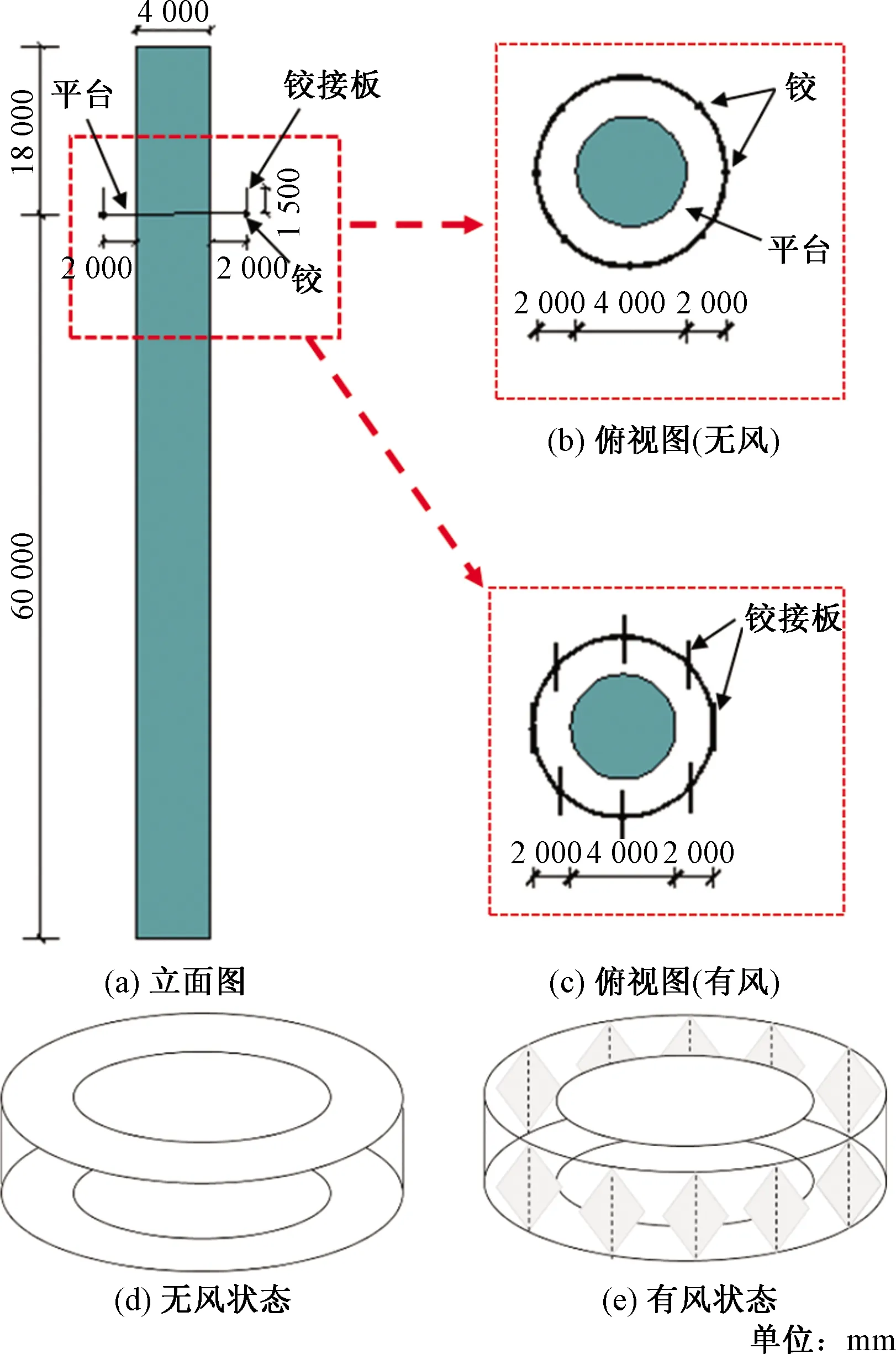
图2 活动式破风圈示意图

该烟囱总高度为78 m，直径为4 m，壁厚为0.018 m，壳体材料选用Q235B钢材，材料参数为：钢材密度7 850 kg/m3；泊松比为0.3；弹性模量为206 GPa。地震设防烈度为7度，基本地震加速度0.15g，场地类型为Ⅱ类场地，地面粗糙度为B类，地面粗糙度系数为0.16，根据《建筑结构荷载规范》(GB 50009—2012)[14]可知，该地区基本风压(按10年重现期)为0.55 kN/m2，由式(1)计算可知，该地区10年一遇风荷载下的平均风速为22.13 m/s。

(1)

式(1)中：ω0为风压，Pa；v0为风速，m/s；ρ为空气密度，取1.225 kg/m3。

2 钢烟囱圆柱绕流分析

当风吹过建筑物会在建筑物后方产生交替脱落的漩涡，从而加大结构的振动，一般流体控制的方法主要分为主动控制方法和被动控制方法，采用被动控制方法，通过在圆柱周边布置可调节长度的、活动式的、类似于破风圈结构的板，破坏流体在边界分离后涡结构的形成。

涡流是通过漩涡脱落频率来描述的，而漩涡脱落频率与斯特罗哈数及结构计算区域长度与来流速度相关。

(2)

式(2)中：f为漩涡脱落频率；Sr为斯特劳哈尔数，圆截面结构取0.2；v为来流速度；D为结构直径。

利用ADINA软件，对结构进行二维圆柱绕流模拟，来模拟风吹过该结构后的绕流现象，主要参数设定如下。

(1)边界条件：流场入口处采用速度入口边界，出口采用Outflow边界，上下边界及圆柱表面采用固定壁面Wall边界，设定为不可滑移。

(2)网格划分：采用计算流体动力学(computational fluid dynamics,CFD)模块对结构进行网格划分，网格单元总数为15 000，节点总数为15 300。

(3)单元设定及流体模型计算参数：选用FCBI-C单元，二阶空间离散方法，时间积分方法选择Composite，此方法更容易使扰流发生涡激脱落现象。

(4)参数设定：空气密度为1.225 kg/m3；空气黏度为1.789 4×105。二维流场网格划分如图3所示。

D为结构直径；L为板的长度

根据赤峰地区不同重现期的基本风速，脉动风速谱频率的取值范围为0.001～6 Hz，采用Davenport谱模拟时长为100 s的脉动风速谱，得到的赤峰地区10、50、100年重现期平均风速分别为22.13、29.97、32.58 m/s。考虑结构的临界风速大小与赤峰市的风速条件，将输入风速设定为22、28、34 m/s。研究钢烟囱在3种风速下的圆柱绕流现象。分别计算不同风速条件对应的雷诺数与漩涡脱落频率，如表1所示。

表1 不同风速下雷诺数与漩涡脱落周期对比

在3种不同风速下的雷诺数均大于3.5×106，漩涡脱落周期分别为0.91、0.71、0.59，22 m/s风速下漩涡脱落周期更接近结构的自振周期1.36 s，对结构自振影响较大。

调节板长度L，根据结构钢烟囱直径D选取L=D、L=2D、L=3D3种不同长度进行简化模拟，调节板宽度统一取0.1 m，提取结构速度云图如图4所示。

图4 钢烟囱速度云图

由速度云图(图4)可以看出，当风进入模拟流场区域吹过烟囱时，流场发生了显著变化。绝大部分气流绕过烟囱继续向前运动，在背风面速度较大，并相继出现漩涡，绕流区域的风速最大值出现在结构的斜后方。

改变调节板长度L及设置数量N，来对比钢烟囱速度流线图，如图5所示。可以看出，在加入可调节的活动式破风圈之后，流场的速度发生了显著变化，改变了尾流形状，起到一定破涡作用，从而消除卡门涡街。不同工况的速度时程曲线如图6所示，可以看出，当调节板长度为直径2倍，设置数量为3时，即分别设置在上部、下部、及正后方时，效果最佳。

图5 流场的速度流线图

图6 结构速度时程图

3 结构动力响应作用分析

3.1 有限元模型建立

在数值风洞模拟过程中，结构与流体间存在相互作用，即结构在流体作用下会产生变形，这种变形会反过来影响流体载荷的分布和大小，所以在模拟过程中应考虑流固耦合效应，建立“风场-结构”双向流固耦合模型。

在选取流场尺寸时，为避免模拟结果失真，需满足阻塞率小于3%的要求，因此选取流场域尺寸为200 m×200 m×120 m，模型位于计算域中心，来流风流向从-Y→+Y，流场模型如图3所示。结构部分采用shell单元建模；流体部分选用3D-Fluid单元，空气按照不可压缩流体进行设置，湍流模型采用RNGk-ε模型(k为湍动能，ε为耗散率)，定义流体材料时，空气密度ρ=1.225 kg/m3,空气黏度μ=17.9×10-6Pa·s。流体特殊边界定义为Wall和Fluid-structure-interface边界，活动式破风圈有限元模型如图7所示。

图7 钢烟囱流场模型

3.2 无活动式破风圈结构自振特性分析

采用子空间迭代法对钢烟囱进行模态分析，来确定结构的频率、周期与振型，提取前10阶频率与周期结果，如表2所示。钢烟囱结构第1、2阶振型以水平方向平动为主，第3、4阶振型以水平方向弯曲与扭转为主。

表2 钢烟囱自振特性参数

3.3 横风向风振作用分析

当风吹过塔设备后，将会在塔体的背后产生旋涡，这种旋涡通常称为卡曼旋涡。卡曼漩涡的产生会使结构表面的压力呈周期性的变化，形成横向力，加大结构的振动[15]，形成机理如图4所示。当横风向漩涡脱落频率与结构某一阶自振频率接近或相同时，会产生横风向共振。

《建筑结构荷载规范》(GB 50009—2012)[14]中规定，对于圆形截面且竖向斜率不大于2%的结构或构件需进行横风向共振响应分析，判别准则如下。

(1)当雷诺数Re<3×105且1.2νH>νcr,j时(νH为烟囱顶部H处风速，νcr,j为第j振型的共振临界风速)，可能发生第1阶振型微风共振(亚临界范围的共振)，此时应在构造上采取防振措施或控制结构的临界风速νcr不小于15 m/s，以降低微风共振的发生率。

(2)当雷诺数Re>3×106且1.2νH>νcr,j时，可能发生横风向共振(跨临界范围的共振)，此时应验算共振响应。

(3)当雷诺数3×105≤Re<3×106时，发生超临界范围的共振，此时可不做处理。

选取有限元软件模拟结构的前四阶自振周期进行分析计算，雷诺数Re、临界风速νcr和结构顶部风速νH计算公式分别为

Re=69 000νD

(3)

(4)

(5)

式中：νcr,j为第j振型的共振临界风速，m/s；为计算所用风速，取临界风速；D为结构截面直径,m，当结构的截面沿高度缩小时(倾斜度不大于0.02°)，可近似取2/3结构高度处的直径；Sr为斯托罗哈尔数，无量纲系数，对圆截面结构取0.2；Tj为第j振型自振周期，s；νH为烟囱顶部H处风速，m/s；μH为结构顶部H处风压高度变化系数，无量纲；ω0为基本风压，kN/m2。

计算后结构的横风向判别结果如表3所示。

表3 横风向风振判别

由表3可知，前4阶振型的雷诺数均大于3×106，但只有前两阶振型1.2νH大于临界风速νcr，后4阶振型1.2νH均小于临界风速νcr，根据校核准则，只有前两阶振型会发生强风共振。

3.4 位移加速度时程响应分析

高耸圆截面结构在低风速作用下会同时产生作用方向和风向方向相同的顺风向作用和垂直于风向的横风向作用，施加赤峰市当地10年一遇基本风速为22.13 m/s的脉动风，提取钢烟囱结构与设置风见鸡结构的顶部的顺风向位移、横风向移、顺风向加速度及横风向加速度时程曲线如图8所示。

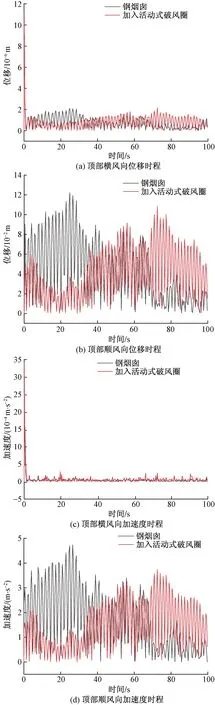
图8 顶部时程曲线

可以看出，在22.13 m/s的风速下，当风向角为0°时，无活动式破风圈钢烟囱的顶部顺风向最大位移为-0.122 2 m，位于结构顶部；横风向最大位移为1.125×10-5m，同样位于顶部；顺风向最大加速度为4.738 m/s2；横风向最大加速度为0.001 57 m/s2。

加入活动式破风圈后，在同样22.13 m/s的风速下，当风向角为0°时，钢烟囱的顶部顺风向最大位移为0.108 2 m，位于结构顶部；横风向最大位移为1.059×10-5m，同样位于顶部；顺风向最大加速度为3.748 m/s2；横风向最大加速度为0.003 42 m/s2。两种工况下的位移、加速度幅值对比如表4所示。

由表4对比结果可知：设置活动式破风圈后的钢烟囱较原钢烟囱最大横风向位移、顺风向位移、顺风向加速度均有减小作用，减小幅度分别为5.8%、11.46%、20.89%，但横风向加速度无显著减小作用。可见，该措施对于减小结构顺风向响应有一定效果，横风向响应减小不太明显。

表4 设置活动式破风圈前后响应对比

采用快速傅里叶变换(fast fourier transform,FFT)方法，对结构位移时程数据进行频谱分析，如图9所示。可以看出，加入活动式破风圈结构后部分低频振型被激起，高频振型有小幅度变化，但变化不大，主频率对应的动力响应大大降低。

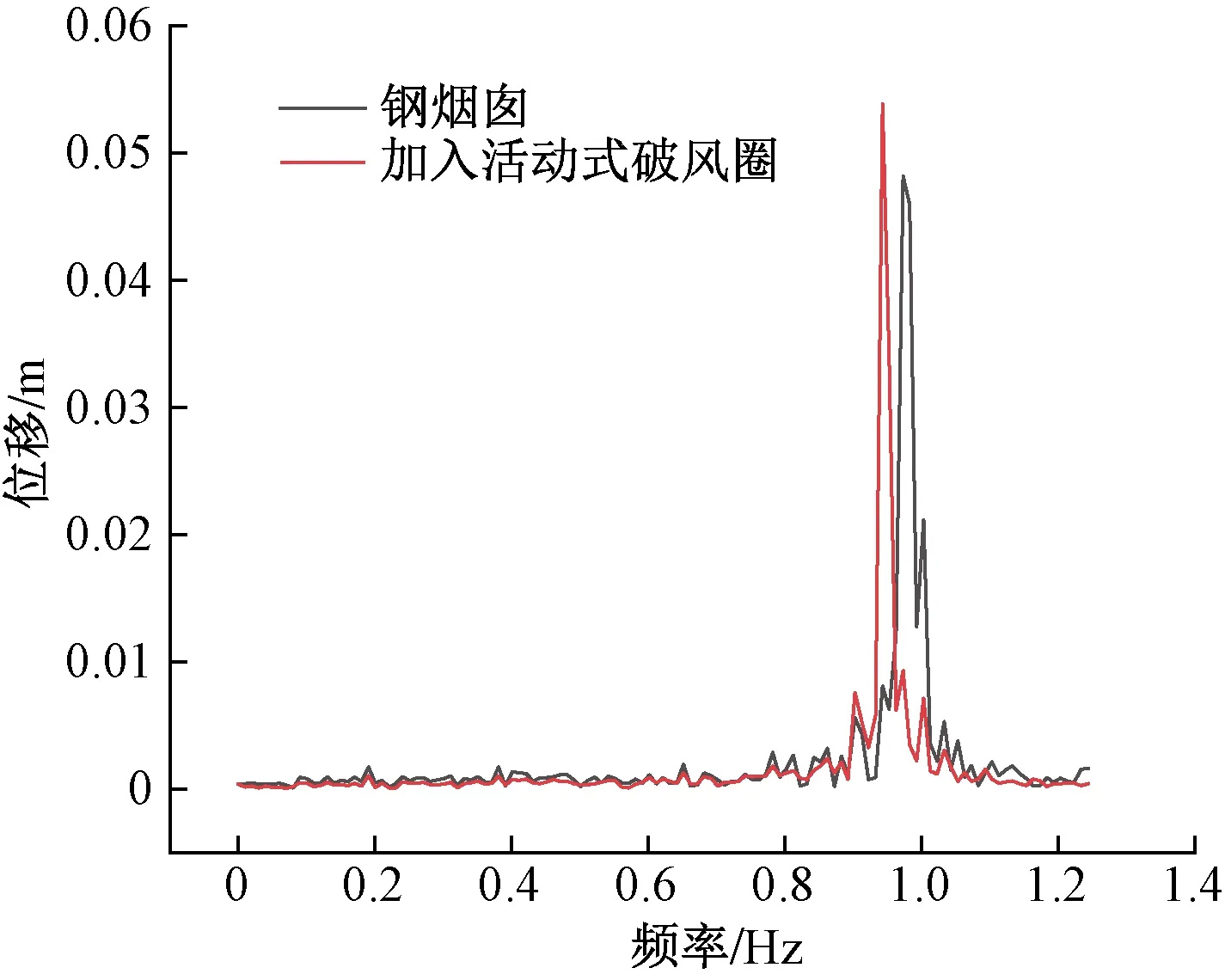
图9 位移反应谱曲线

提取结构不同标高处的位移、加速度如图10、图11所示。可以看出，在加入活动式破风圈后，钢烟囱在不同标高处的位移、加速度均有减小作用。且随着高度的增加，位移、加速度减小幅度均增大。

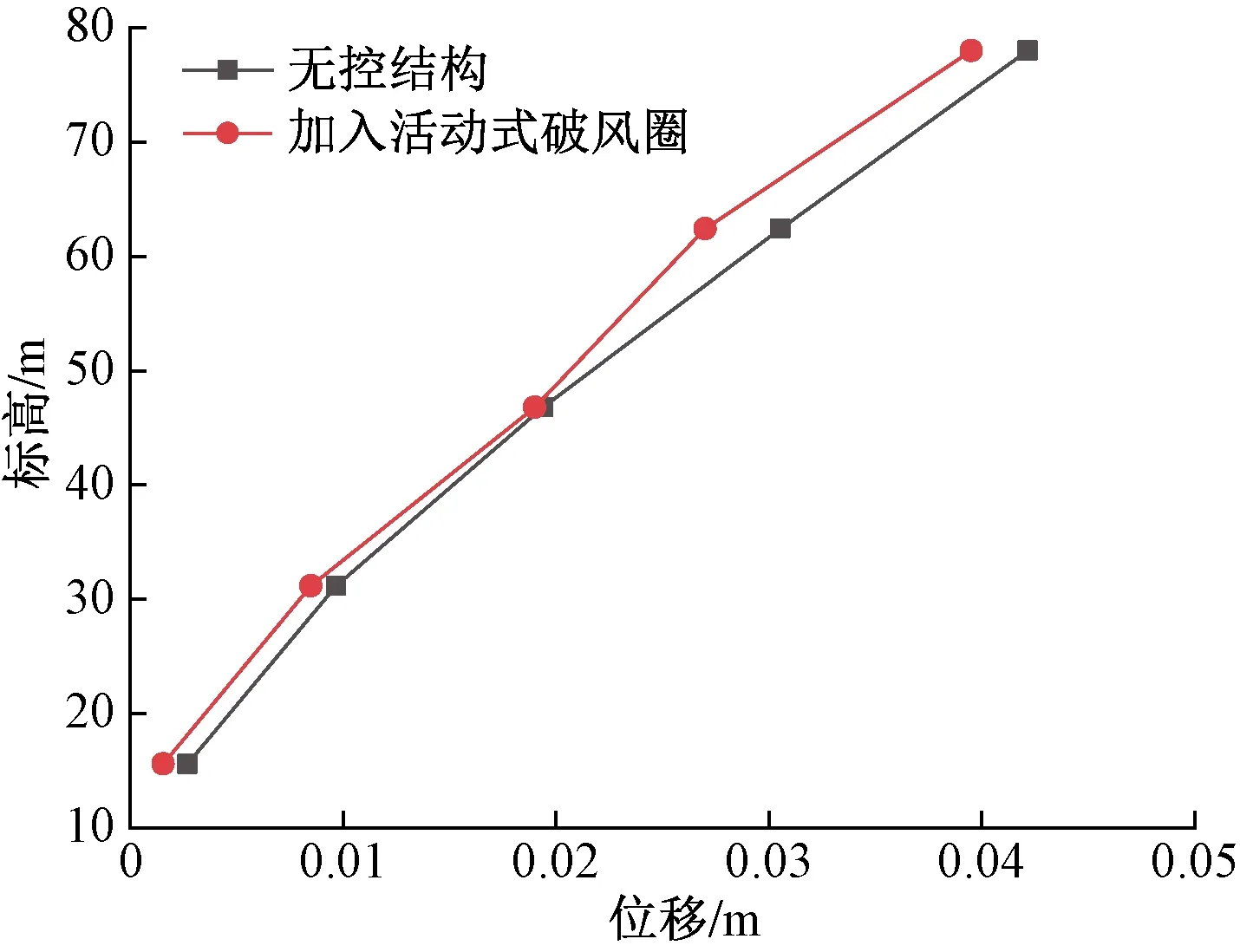
图10 各标高处顺风向位移

图11 各标高处顺风向加速度

4 结论

对于高耸结构产生的结构振动问题，结合实际工程，在现有的楼梯平台的基础上，通过设置可调节活动式板，对结构的动力响应作用与圆柱绕流现象进行分析，提出一种结构减振措施，可为工程设计提供参考，主要得到以下结论。

(1)通过对钢烟囱结构进行横风共振的判别，根据规范中的校核原则，钢烟囱只有前两阶振型会发生强风共振，不需考虑其他振型的作用。

(2)设置可调节活动式破风圈结构后，相对于无控结构，其顺风向加速度、顺风向位移均有减轻作用，减振率分别达到11.46%、20.89%，对结构横风向响应的影响不大。说明此措施对于减轻结构涡振有一定效果。

(3)通过模拟二维圆柱绕流，通过改变调节板长度及设置数量，分析其速度的变化规律，结果显示当调节板长度设置为直径2倍、设置数量为3时，效果比较明显。