Alternative non-Gaussianity measures for quantum states based on quantum fidelity
Cheng Xiang(向成) Shan-Shan Li(李珊珊) Sha-Sha Wen(文莎莎) and Shao-Hua Xiang(向少华)
1College of Electrical and Information Engineering,Huaihua University,Huaihua 418008,China
2Hunan Provincial Key Laboratory of Ecological Agriculture Intelligent Control Technology,Huaihua 418008,China
Keywords: non-Gaussianity,quantum fidelity,non-Gaussian states,sine metric
1. Introduction
Non-Gaussianity of quantum states is a useful resource in quantum information schemes with continuous variables since such a property can be exploited to improve their performances, including quantum teleportation,[1-3]quantum cloning,[4]entanglement distillation,[5,6]quantum secure communication,[7]and estimation problem.[8]To quantify non-Gaussianity,some metrics have been introduced over the past ten years. For example, Genoniet al.proposed the Hilbert-Schmidt[9]and the relative entropy measures[10]of non-Gaussianity for quantum states. Ivanet al.defined another non-Gaussianity measure by means of the Wehrl entropy.[11]Very recently, Fuet al.introduced a novel measure for non-Gaussianity of bosonic field states in terms of the Wigner-Yanase skew information.[12]According to the metric axioms,[13]one sees that all such metrics do not satisfy the symmetry and except the Hilbert-Schmidt metric, all the other ones are boundless,thus giving rise to a huge challenge of measuring it experimentally. Therefore, it is highly desirable to look for a plausible measure of non-Gaussianity.
In quantum information theory, non-Gaussianity quantifies a departure of a given quantum state from its reference Gaussian state. When talking about the issue of discriminating two different quantum states, we focus naturally on quantum fidelity, which provides a quantification of the degree of similarity of a pair of quantum states and has many attractive properties.[14]The fidelity was originally defined as Uhlmann’s transition probability.[15]When one of two quantum states is pure, the fidelity is easily computable and reduces to their overlap. However, for an arbitrary pair of mixed states, the fidelity involves successive computation of the square roots of Hermitian matrices, which is in general hard to compute analytically. In order to avoid this difficulty, Wanget al.introduced an alternative fidelity for two mixed quantum states,[16]which satisfies Jozsa’s four axioms up to a normalization factor[14]and is relatively easy to be calculated. As is well known, quantum fidelity is not a metric, but can easily be used to define many metrics on the space of quantum states such as the sine distance,[13]the Bures angle,[17]and the Bures distance.[18]For convenience,we shall refer these metrics as the fidelity-based ones,which have been widely used to quantify the non-classicality,[19]quantum entanglement,[20]and quantum discord of quantum states.[21]Motivated by these ideas,in this paper,we would like to quantify the non-Gaussianity of quantum states using these fidelitybased metrics together with quantum fidelity introduced by Wang.[16]To the best of our knowledge, there are currently few studies examining this problem.
The paper is organized as follows.In Section 2 we review some known quantum fidelities as well as fidelity-based metrics,and elucidate their fundamental properties. We introduce our measures for non-Gaussianity. Using these measures, we assess the non-Gaussianity of some relevant single-mode and two-mode quantum states in Section 3. At the same time,we analyze the consistency of these fidelity-based measures. In Section 4,we devote attention to a comparison between all the known metrics for non-Gaussianity in the literature and discuss their legitimacy according to the metric axioms. Finally,we summarize our main results in Section 5.
2. Non-Gaussianity measures based on fidelity
Let us consider the fidelity, which is of importance in quantum information science[17]and other fields such as quantum chaos[22]and quantum phase transitions.[23,24]According to Uhlmann,[15]the fidelity of any two quantum statesρandσis defined as


As a metricδ(ρ,σ)defined on quantum states,it should satisfy the basic properties: (i) non-negativity:δ(ρ,σ)≥0,andδ(ρ,σ)=0 if and only ifρ=σ, (ii) symmetry under swapping of the two states:δ(ρ,σ)=δ(σ,ρ), and triangle inequality:δ(ρ,σ)+δ(τ,σ)≥δ(ρ,τ) for all statesρ,σandτ. It has been shown in Ref. [25] that for the Uhlmann-Jozsa fidelity, these three metrics are genuine ones. For the super-fidelity,C(ρ,σ) preserves the metric properties, while bothA(ρ,σ) andB(ρ,σ) do not always satisfy the triangle inequality. Hence, one needs to study whether or not these measures obey the above-mentioned metric conditions with Wang’s quantum fidelityFW(ρ,σ)given by Eq.(4). It can be easily seen that the above-mentioned metrics share naturally the first two properties. Thus, we shall prove separately their triangle inequalities.
Theorem 1 Letρ,σ, andτbe the density matrices of any three quantum states. The following triangle inequality for Bures angle holds:


To prove inequality(15),we consider two cases:



Note that for an arbitrary quantum operation described by a completely positive trace-preserving (CPTP) mapε:(ρ),we haveF(ε(ρ),ε(σ))≥F(ρ,σ).[17]Hence,our introduced non-Gaussianities monotonically decrease under Gaussian quantum channels,that is,δNG(εGρ)≤δNG(ρ).
Lemma 3 Consider a bipartite factorized stateρ=ρ1⊗ρ2. Ifρ2is a Gaussian state,thenδNG(ρ1⊗ρ2)=δNG(ρ1).
Proof For a bipartite factorized stateρ12=ρ1⊗ρ2, its reference Gaussian state can be written asρ12,rG=ρ1,rG ⊗ρ2,rG. According to the definition of the purity of a quantum state,we have

which concludes the proof.
Lemma 4 Our non-Gaussianities satisfy the symmetry under the swapping of arbitrary two quantum statesρandσ:δNG(ρ,σ)=δNG(σ,ρ).
Proof As a matter of fact,the proof follows easily from the definition ofFW(σ,ρ),which also has the exchange symmetry.
3. Examples
In this section,by means of the quantum fidelity given by Eq. (4), we use the mentioned-above metrics to evaluate the non-Gaussianity of some relevant single-mode and two-mode non-Gaussian states,e.g.,single-mode mixture of Fock states,Schr¨odinger-cat-like states (SCLSs), and two-mode Bell-like states,by which we investigate the consistency between these non-Gaussianity measures and discuss their success.
3.1. Single-mode mixture of Fock states
We begin by considering a special family of single-mode non-Gaussian mixed states: statistical mixtures of the vacuum state andn-photon Fock state defined by

SubstitutingFWinto Eqs.(5)-(7),we finally evaluate the non-Gaussianity of single-mode mixture of Fock states. The results are reported in Fig. 1 as a function ofpand for different values of photon numbern. From the plots, all of the above three non-Gaussianity metricsδNGare naturally null fornp=0, corresponding to vacuum state, as is expected. One can also see that the three non-Gaussianity measures exhibit a monotonically increasing behavior with the number of photonsnand the parametersp.For a case ofnp ≪1,they present

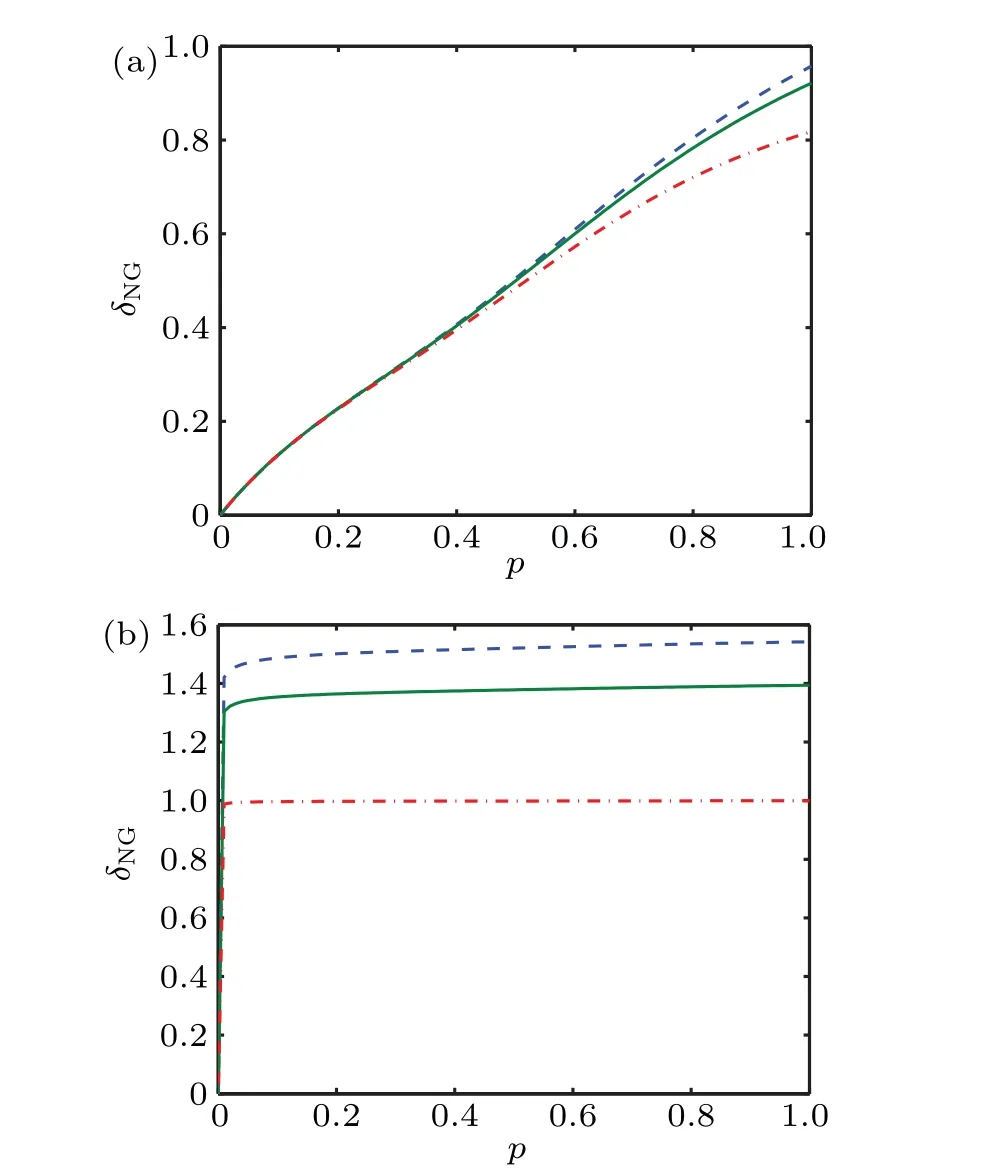
Fig.1. Non-Gaussianity δNG of mixtures of the vacuum and n-photon Fock states as a function of n and p: (a) n=2, (b) n=400000. The dashed line corresponds to A(ρ,σ), the solid line to B(ρ,σ), and the dash-dotted line to C(ρ,σ).
3.2. Single-mode photon-added thermal states
The photon addition and subtraction are an important technique for generating quantum non-Gaussian state. Here we consider another family of single-mode non-Gaussian mixed states:m-photon-added thermal states (mPATSs),which are defined as[11,30]



Fig.2. Non-Gaussianity δNG of mPATSs as a function of x and for different values of the added photons m: (a)m=1,and(b)m=10. Curve types are the same as in Fig.1.
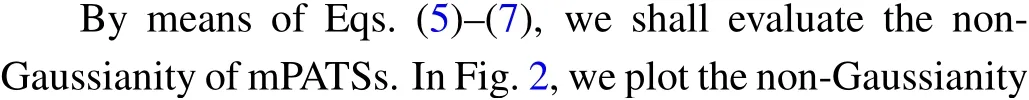

3.3. Schr¨odinger-cat-like states
Let us consider single-mode Schr¨odinger-cat-like states,which are represented by a coherent superposition of two coherent states|α〉and|-α〉,as follows:[19]

and the covariance matrix is calculated to be
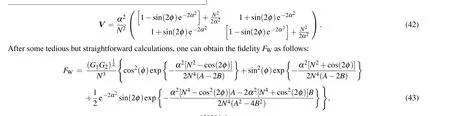



Fig. 3. Non-Gaussianity for single-mode SCLSs as a function of the parameter φ and for different values of the amplitude α: (a)-(d) α ={0.2,0.4,1.5,5}. Curve types are the same as in Fig.1.
3.4. Two-mode Bell-like states
As our final example, we focus on two-mode Bell-like states,which are written as

We can obtain that all the first moments of two-mode Bell-like states are zero but their covariance matrices are different from each other. For the states(45a),the covariance matrix is given by

whereI2is a 2×2 unity matrix andσ3=Diag(1,-1).
We proceed to calculate the fidelityFWaccording to the calculation strategy as pervious subsections,obtaining the result



Fig. 4. Non-Gaussianity δNG and concurrence Cen of two-mode Belllike states(a)|Φ〉AB and(b)|Ψ〉AB as a function of θ for θ ∈[-π,π].The dotted line stands for Cen,and other curve types are the same as in Fig.1.
4. Comparison of non-Gaussianity measures

Before ending our work, we compare our fidelitybased non-Gaussianity measures with several known measures which have been introduced in the last ten years. Based on the Hilbert-Schmidt distance,Genoniet al.first proposed the following measure of non-Gaussianity of a stateρ:[9]andρ2, regardless of which measure we choose. This is because Fock state is a one-parameter categories of states and its non-Gaussianity has a monotonic behavior with respect to the photon numbersn. However,for a case of multi-parameter quantum states, the conclusion may not be correct. On the other hand,it is apparent from Table 1 that different measures have different limiting values of non-Gaussianity, in particular, the measuresδB,NW(ρ), andNG(ρ) are boundless. As is well-known, it is highly desirable that the chosen metric should be a normalized one,that is,its maximum value is equal to one. According to this point, we think that among these measures,C(ρ,σ)is an optimal non-Gaussianity measure for quantum states and then expect that it can be applied to investigate the non-Gaussianity-bounded uncertainty relation[32]and quantum communication.[7,37]
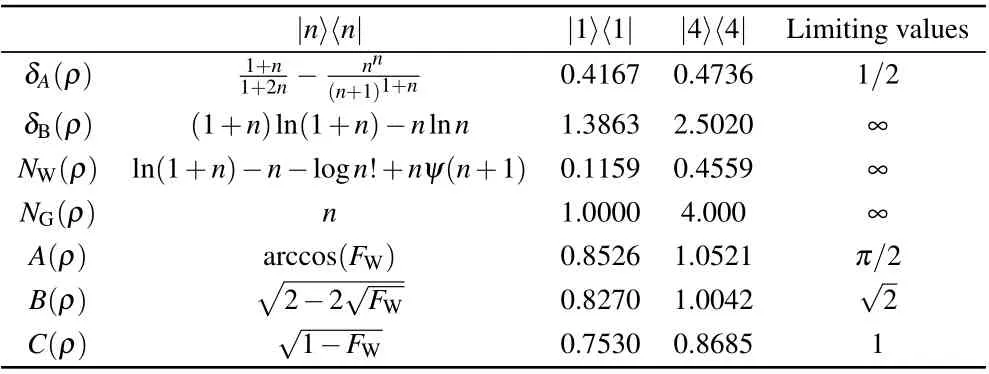
Table 1. Comparison of non-Gaussianity measures for Fock states.
5. Conclusion
With the quantum fidelity introduced by Wang, we have presented three alternative measures of non-Gaussianity: the sine distance, the Bures angle, and the Bures distance. We have further evaluated the non-Gaussianity of some relevant single-mode and two-mode non-Gaussian states using these fidelity-based measures. We have shown that such measures are capable of precisely evaluating the non-Gaussianity of a wide range of non-Gaussian quantum states,particularly even Schr¨odinger-cat-like states,and have a very good consistency in displaying non-Gaussian behaviors. Finally, we have focused on the comparison between our introduced measures and the celebrated non-Gaussianity ones according to the metric axioms. We have also shown that the sine distance can be regarded as the best“legitimate”measure for non-Gaussianity of quantum states among all.
Although much work has been carried out,the problem of quantifying non-Gaussianity of quantum states remains completely unsolved to date. This is because the popular measures are hard to meet with all the six requirement of metric. In particular, they are required to have a straightforward physical interpretation and be feasible in an experiment. Therefore,our result may shed certain light on the quantitative aspect of non-Gaussianity of quantum states and we hope that our introduced measures have the potential applications in quantum information technologies.
Acknowledgements
Project supported by the Natural Science Foundation of Hunan Province,China(Grant No.2021JJ30535),the Science and Technology Innovation Foundation for College Students in Hunan Province of China(Grant No.2020RC1013),and the Research Foundation for Young Teachers from the Education Department of Hunan Province of China(Grant No.20B460).
- Chinese Physics B的其它文章
- Measurements of the 107Ag neutron capture cross sections with pulse height weighting technique at the CSNS Back-n facility
- Measuring Loschmidt echo via Floquet engineering in superconducting circuits
- Electronic structure and spin-orbit coupling in ternary transition metal chalcogenides Cu2TlX2(X =Se,Te)
- Characterization of the N-polar GaN film grown on C-plane sapphire and misoriented C-plane sapphire substrates by MOCVD
- Review on typical applications and computational optimizations based on semiclassical methods in strong-field physics
- Quantum partial least squares regression algorithm for multiple correlation problem

