GENERALIZED CES`ARO OPERATORS ON DIRICHLET-TYPE SPACES*

Jianjun JIN (金建军)

School of Mathematics Sciences，Hefei University of Technology，Xuancheng Campus，Xuancheng 242000，China;E-mail:jin@hfut.edu.cn

Shuan TANG (唐树安)

School of Mathematics Sciences，Guizhou Normal University，Guiyang 550001，China E-mail:tsa@gznu.edu.cn

Abstract In this note，we introduce and study a new kind of generalized Cesàro operator，Cμ，induced by a positive Borel measure μ on[0，1) between Dirichlet-type spaces.We characterize the measures μ for which Cμ is bounded (compact) from one Dirichlet-type space，Dα，into another one，Dβ.

Key words generalized Cesàro operator;Dirichlet-type spaces;Carleson measure;boundedness and compactness of operator

1 Introduction

Let D be the unit disk in the complex plane C.We use C，C1，C2，···to denote universal positive constants that might change from one line to another.For two positive numbers A and B，we write A≤B or A≥B if there exists a positive constant C independent of A and B such that A≤CB or A≥CB，respectively.We will write A≍B if both A≤B and A≥B.

We denote by H (D) the class of all analytic functions on D.For 0＜p＜∞，the Hardy space Hpis the class of all f∈H (D) such that

For α∈R，the Dirichlet-type space，denoted by Dα，is defined as

When α=0，D0coincides the classic Dirichlet space D，and when α=1，D1becomes the Hardy space H2.

The Cesàro operator，which is an operator on spaces of analytic functions acting on the Taylor coefficients，is defined，for f=∈H (D)，as

The boundedness and compactness of the Cesàro operator and its generalizations defined on various spaces of analytic functions like Hardy spaces，Bergman spaces and Dirichlet spaces has attracted much attention (see，for example，[1-10]and the references therein).

In this note，we consider the boundedness and compactness of the Cesàro operator between the Dirichlet-type spaces.We denote N0=N∪{0}.For when 0＜α＜2.For f=∈Dα，by Cauchy’s inequality，we obtain that，for n∈N0，

For 0＜α＜2，it is easy to see that

Consequently，we get，from (1.1) and (1.2)，that

We notice that，for k∈N0，

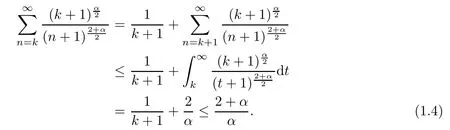
It follows from (1.3) and (1.4) that

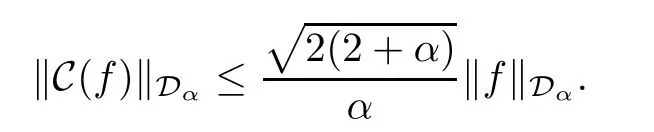
This means that C:Dα→Dαis bounded for 0＜α＜2.We have proved the following:

Proposition 1.1If 0＜α＜2，then the Cesàro operator C is bounded from Dαinto itself.

It is natural to ask whether the Cesàro operator is still bounded from Dαinto Dβ，when αβ.

We observe that the Cesàro operator C is not bounded from Dαinto Dβif α＞β and 0＜α＜2.Actually，if 0＜α＜2 and α＞β，letting 0＜ε＜α and setting f=with

it is easy to see that

Since 0＜α＜2 and 0＜ε＜α，we see that

We note that

and

Then we conclude from (1.5) that there is a constant N∈N such that

If C:Dα→Dβis bounded，then there exists a constant C1＞0 such that

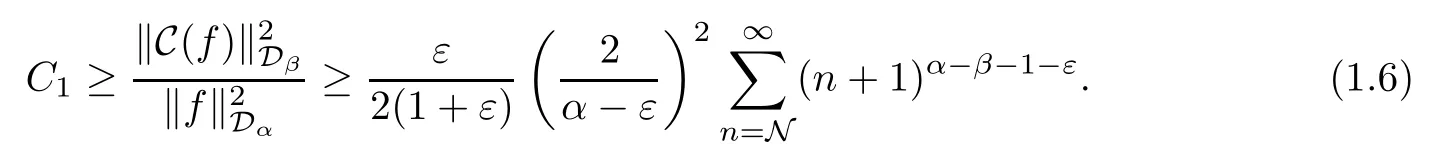
However，when ε＜min{α-β，α}，we see that

Hence we get that (1.6) is a contradiction.This means that the Cesàro operator C is not bounded from Dαinto Dβif α＞β and 0＜α＜2.

We note that

Let μ be a positive Borel measure on[0，1).For f=∈H (D)，we define the generalized Cesàro operators Cμas

where

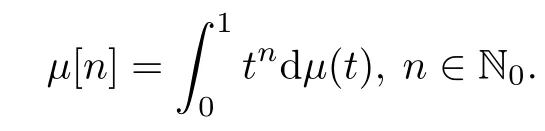
In this paper，we first study the question of characterizing measures μ such that Cμ:Dα→Dβis bounded.We obtain a sufficient and necessary condition of μ for which Cμ:Dα→Dβis bounded.

To state our first result，we introduce the notation of a generalized Carleson measure on[0，1).Let s＞0 and let μ be a positive Borel measure on[0，1).We say that μ is an s-Carleson measure if there is a constant C2＞0 such that

μ([t，1))≤C2(1-t)s

for all t∈[0，1).

Now we can state the first main result of this paper.

Theorem 1.2Let 0＜α，β＜2.Then the following statements are equivalent:

(1) Cμ:Dα→Dβis bounded;

(3) there is a constant C3＞0 such that

for all n∈N0.

The proof of Theorem 1.2 will be given in the next section.We shall characterize a measure μ such that Cμ:Dα→Dβis compact in the last section.

2 Proof of Theorem 1.2

In our proof of Theorem 1.2，we need Beta function defined as follows:

It is known that

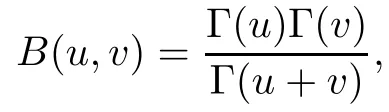
where Γ is the Gamma function defined as

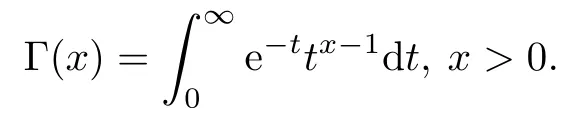
For more detailed information on the Beta function and the Gamma function，see[11].

(2)⇒(3) We note that (3) is obvious when n=0.We get，from integration by parts，that for n (≥1)∈N，

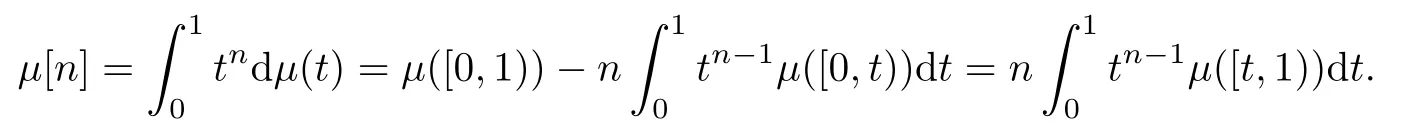
for all t∈[0，1).

It follows that

Here we have used the fact that

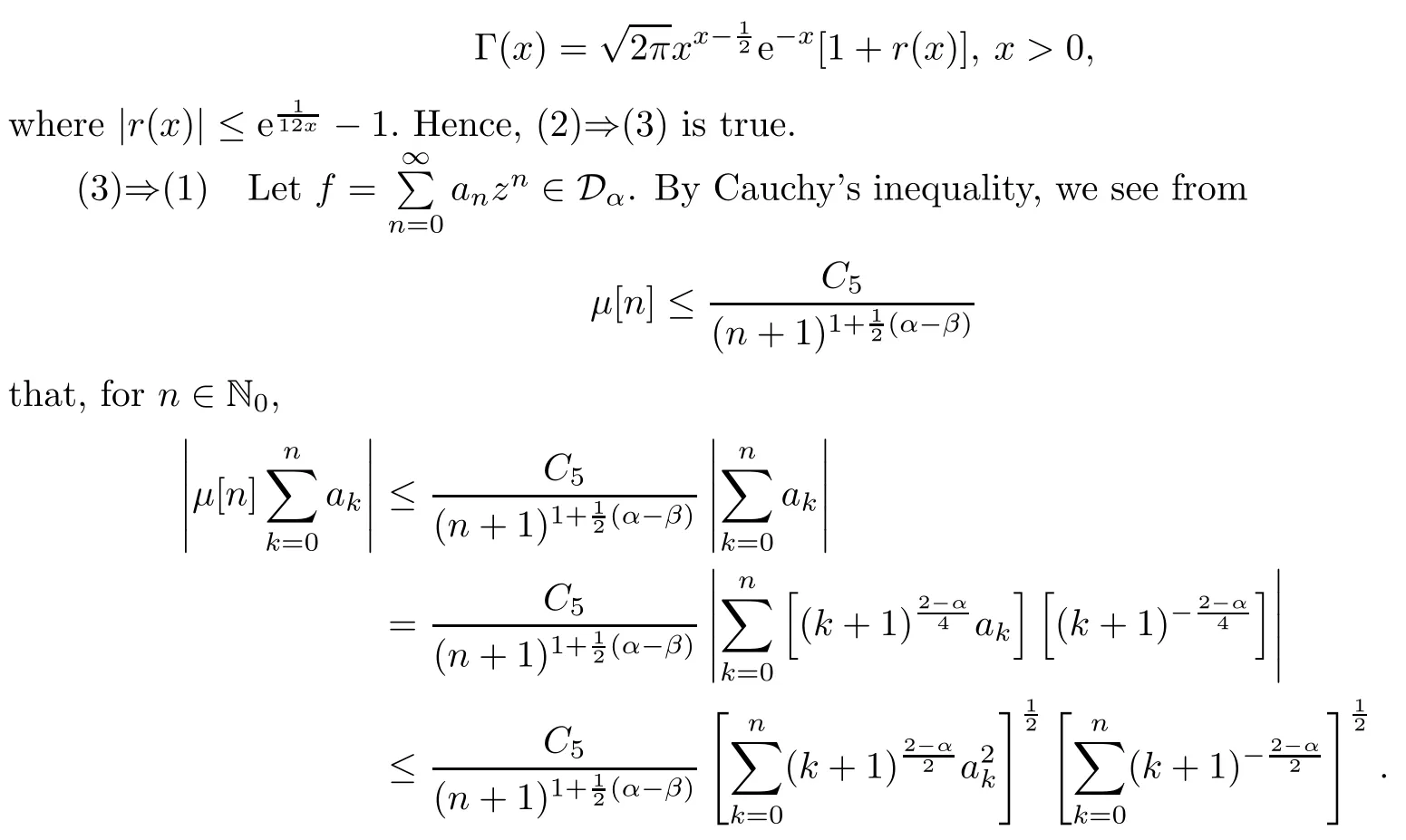
Consequently，we obtain from (1.2) that

Then it follows from (1.4) that

This proves (3)⇒(1).

(1)⇒(2) We need the following estimate presented in[12]:let 0＜t＜1，for any c＞0，we have that

For 0＜b＜1，let N be a natural number.We setwith

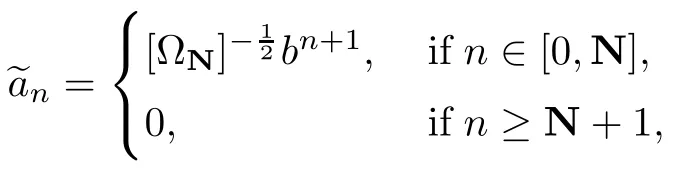
where

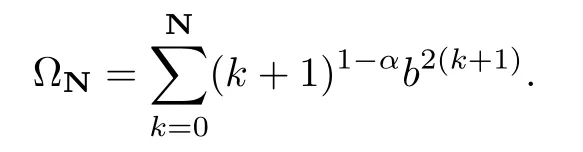
Then it is easy to see that=1.We set SN={k∈N0:k≤N}.In view of the boundedness of Cμ:Dα→Dβ，we obtain that

On the other hand，we note that，when n≤N，

Then we get that

It follows from (2.2) that

Taking N→∞in (2.3)，we see that

for all b∈[0，1).Then we conclude from (2.1) that

This implies that

for all 0＜b＜1.It follows that μ is a[1+]-Carleson measure on[0，1)，and (1)⇒(2) is proved.The proof of Theorem 1.2 is now finished.

3 Compactness of the Generalized Cesàro Operators on Dirichlettype Spaces

For 0＜s＜∞，we say that a positive Borel measure μ on[0，1) is a vanishing s-Carleson measure if μ is an s-Carleson measure and satisfies that

The following theorem is the main result of this section:

Theorem 3.1Let 0＜α，β＜2.Then the following statements are equivalent:

(1) Cμ:Dα→Dβis compact;

Proof of Theorem 3.1First note that，by minor modifications of the arguments of (2)⇒(3) in the proof of Theorem 1.2，we can show (2)⇒(3) of Theorem 3.1.

We proceed to prove (3)⇒(1)，for any f=∈Dαand letting N∈N，we consider

In view of

we see that，for any∈＞0，there is an N0∈N such that

for all n＞N0.

Note that

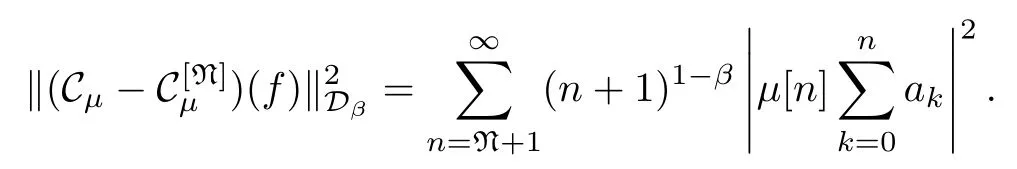
When N＞N0，we get that

Consequently，by using the arguments of (3)⇒(1) in the proof of Theorem 1.2，we see that

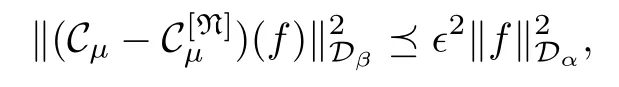
holds for any f∈Dα.Hence，we see that

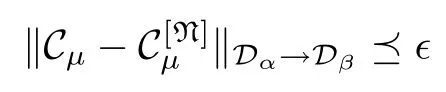
when N＞N0.Here，

where T is a linear bounded operator from Dαinto Dβ.This means that Cμis compact from Dαinto Dβ，and (3)⇒(1) is proved.

Finally，we show that (1)⇒(2)，for 0＜b＜1，we setwith

On the other hand，we have that

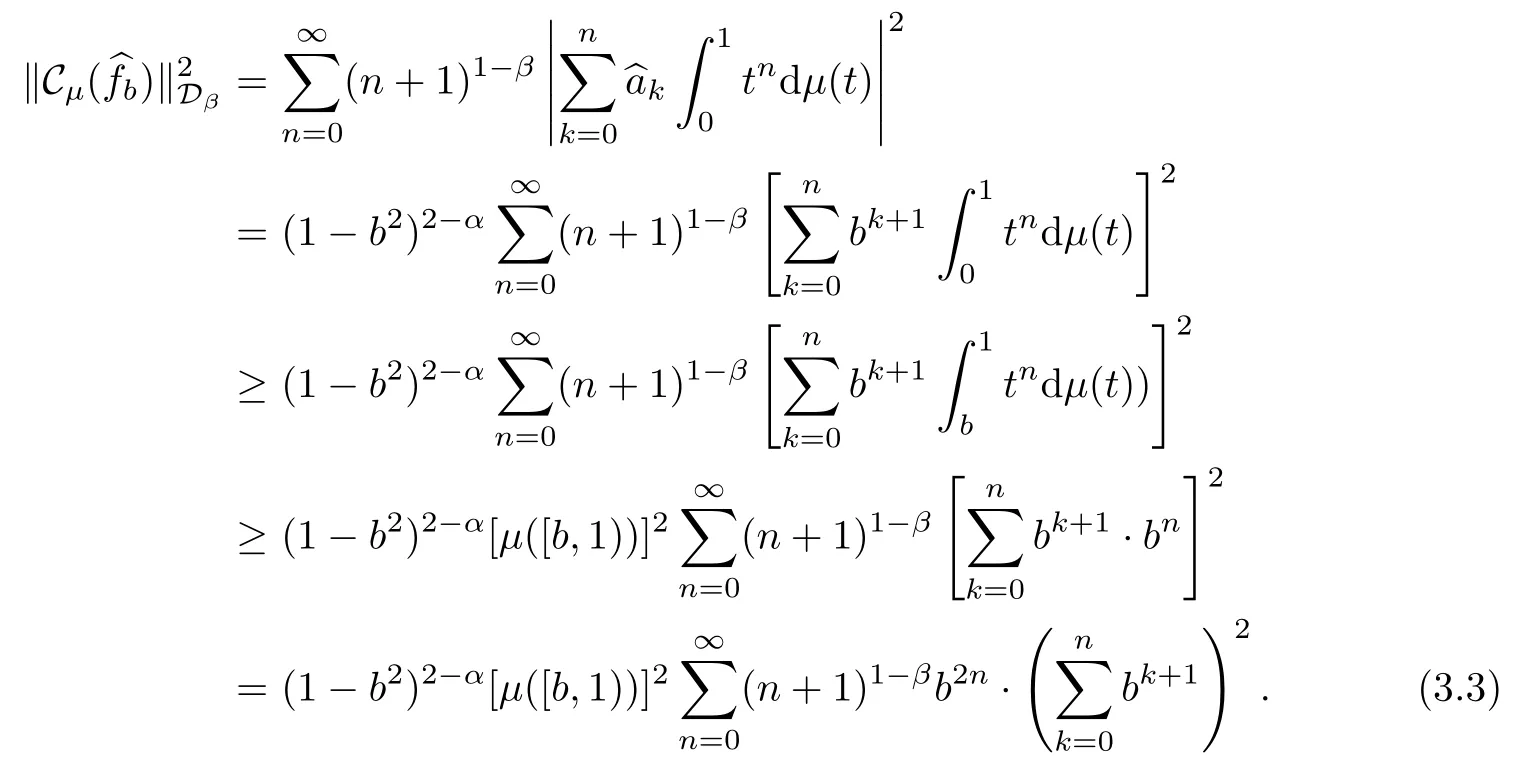
Also，we have that

Combining (3.3) and (3.4)，we see that

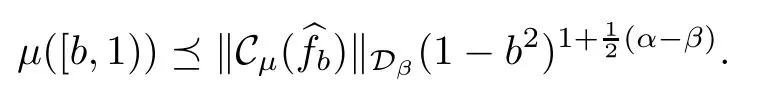
It follows from (3.2) that

This proves (1)⇒(2)，and the proof of Theorem 3.1 is complete. □