区间值T-球形模糊集的距离测度及其应用
李 清,郑婷婷,孙 鑫,王志强
(安徽大学 数学科学学院,安徽 合肥 230601)
为了描述现实生活中的不确定性问题, ZADEH[1]于1965年提出了经典的模糊集 (fuzzy set, FS)理论。 FS理论用[0,1]区间上的数μ来表示每个元素隶属于某个集合的程度,可以较好地体现事物的模糊特征。随后,模糊集理论得到大量的深入研究。ATANASSOV[2]提出了直觉模糊集(intuitionistic fuzzy set, IFS)概念。相比于FS只有一个隶属度函数,IFS增加了一个非隶属度函数,不仅能够表示每个元素关于某个模糊集合的隶属程度μ,也能体现其不属于这个集合的非隶属程度ν,因此对不确定事件的建模更加真实准确。但基于IFS的模型仍存在一定的缺陷,因为它要求满足μ+ν≤1。为了模拟更多真实复杂事物,有时元素对集合的隶属度和非隶属度之和可能超过1。为解决此问题,YAGER[3]提出了毕达哥拉斯模糊集 (pythagorean fuzzy set, PyFS) 的概念,PyFS允许μ2+ν2≤1,可以为元素的模糊性给出更宽泛的特征表示。2017年,YAGER等[4]又提出了更广义的q阶模糊集 (q-rung orthopair fuzzy set,q-ROFS) 的概念,将隶属度和非隶属度的限制拓展到μq+νq≤1 (q≥1)。目前该理论已被广泛应用于多属性决策、模式识别等领域,并取得众多出色成果[5]。
然而,当面对更多数据类型的决策问题时,IFS、PyFS、q-ROFS等模型也有其局限性。比如专家在给一篇文章提出审稿意见时,可能不仅仅是“接受”或“拒绝”,也有可能是“修改”或“不推荐”。针对这种可能,CUONG等[6]提出了图模糊集框架 (picture fuzzy set, PFS),不仅包含元素的隶属度μ与非隶属度ν,还包含犹豫度π,并满足μ+π+ν≤1,从而也可定义拒绝度r=1-μ-π-ν,为处理不确定信息又提供了一个有力的工具。PFS是目前研究成果最为丰富的领域之一,大量学者进行了相关研究。WEI[7]研究了PFS相关的相似性测度并应用于模式识别问题中。SON[8]研究了基于PFS的模糊聚类相关问题。JANA等[9]研究了图模糊聚合算子相关问题并成功应用于多属性决策。与IFS发展过程中存在的问题类似,PFS作为其扩展的模糊集,关于元素的模糊特征范围也在不断深入。但是在某些情形下,如μ=0.3、π=0.5、ν=0.6时,0.3+0.5+0.6>1,这时PFS显然是不适用的。为此,MAHMOOD等[10]提出了球形模糊集 (spherical fuzzy set, SFS) 和T-球形模糊集 (T-spherical fuzzy set, TSFS) 的概念,其中SFS满足μ2+π2+ν2≤1,TSFS满足μq+πq+νq≤1 (q≥1)。相比于PFS和SFS,TSFS更大程度地体现元素的模糊性。当μq+πq+νq=1时,TSFS可以看作是q-ROFS。换句话说,FS、IFS、PFS、SFS和q-ROFS等都可以看作TSFS的特殊情形。
在模糊集理论的实际应用过程中,由于对于元素与某个复杂集合间关系的认知可能是十分模糊的,其中的隶属度、非隶属度、犹豫度也可能无法用精确的数值来表示。采用区间数替代精确的数字可以更好地表示元素对集合隶属程度的原始信息,避免过多的丢失信息。因此,许多学者探讨了各种基于区间数的模糊集情形,如区间值模糊集[11](interval-valued fuzzy set, IVFS)、区间值直觉模糊集[12](interval-valued intuitionistic fuzzy set, IVIFS)、区间值毕达哥拉斯模糊集[13](interval-valued pythagorean fuzzy set, IVPyFS)、区间值q阶模糊集[14](interval-valuedq-rung orthopair fuzzy set, IVq-ROFS)、区间值图模糊集[15](interval-valued picture fuzzy set, IVPFS)和区间值球模糊集[16](interval-valued spherical fuzzy set, IVSFS)等。ULLAH等[17]则将TSFS推广到区间值T-球形模糊集(interval-valuedT-spherical fuzzy set, IVTSFS),将隶属度μ、隶属度ν、犹豫度π的取值由[0,1]中的实数推广至[0,1]中的区间数,使其描述元素的模糊性更加全面,所提出的基于IVTSFS的几种集成算子方法已成功运用于相关的金融投资领域,是目前较为先进且强大的模糊集模型,上述的模糊集都可以看作IVTSFS的特殊情况。
另一方面,距离测度是模糊集研究中的一个重要课题,广泛应用于多属性决策、模式识别、医疗诊断和聚类分析等领域。最广泛应用的距离测度有Hamming距离测度、Euclidean距离测度和广义Euclidean距离测度等。目前许多学者在多种模糊集上建立了距离测度的相关研究[18-19],但基于IVTSFS的相关距离测度研究还十分缺乏,因此探究基于IVTSFS的距离测度相关性质与方法是十分必要的。
1 预备知识
1.1 基本定义

为了方便起见,在不引起混淆的情况下,用(μ,π,ν)表示一个T-球形模糊数(T-spherical fuzzy number, TSFN)。

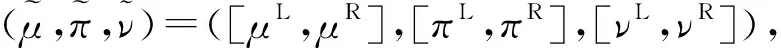
不同情形下的IVTSFS可看作不同的模糊集。①TSFS:若μL=μR=μ,πL=πR=π,νL=νR=ν;②IVSFS:若q=2;③SFS:若q=2,μL=μR=μ,πL=πR=π,νL=νR=ν;④IVPFS:若q=1;⑤PFS:若q=1,μL=μR=μ,πL=πR=π,νL=νR=ν;⑥IVq-ROFS:若πL=1-μR-νR,πR=1-μL-νL;⑦q-ROFS:若μL=μR=μ,νL=νR=ν,πL=πR=1-μ-ν;⑧IVPyFS:若q=2,πL=1-μR-νR,πR=1-μL-νL;⑨PyFS:若q=2,μL=μR=μ,νL=νR=ν,πL=πR=1-μ-ν;⑩IVIFS:若q=1,πL=1-μR-νR,πR=1-μL-νL;IFS:若q=1,μL=μR=μ,νL=νR=ν,πL=πR=1-μ-ν;IVFS:若q=1,νL=1-μR,νR=1-μL;FS:若q=1,μR=μL=μ,νL=νR=1-μ。
1.2 区间值T-球形模糊集的得分因子与精确因子

SC(α)=
AC(α)=
显然SC(α)∈[-1,1],AC(α)∈[0,1]。对任意的两个IVTSFNα和β:①若SC(α)>SC(β),则α≻β。②若SC(α) 定义4设A、B∈IVTSFS(X), 设D是一个映射,D∶IVTSFS(X)×IVTSFS(X)→[0,1]。若满足下列条件:①0≤D(A,B);②D(A,B)=0当且仅当A=B;③D(A,B)=D(B,A);④∀C∈IVTSFS(X),满足D(A,C)≤D(A,B)+D(B,C),则称D(A,B)为A、B之间的一个IVTSFS距离测度。 定义5设X={x1,x2,…,xn},A、B∈IVTSFS(X),则A、B之间的Hamming距离测度定义为: 定义6设X={x1,x2,…,xn},A、B∈IVTSFS(X),则A、B之间的Euclidean距离测度定义为: 定义7设X={x1,x2,…,xn},A、B∈IVTSFS(X),则A、B之间的广义加权距离测度定义为: 对一项投票结果,决策人可能更看重支持的人数,而谨慎考虑反对、中立和弃权人数对结果所造成的影响。所以有理由相信对隶属度、犹豫度、非隶属度和拒绝度进行赋权以得到符合实际决策人偏好的结果。基于这种情况,提出广义二重加权距离测度。 定义8设X={x1,x2,…,xn},A、B∈IVTSFS(X),则A、B之间的广义二重加权距离测度定义为: 考虑到目前还没有学者针对IVTSFS研究相关距离测度问题,选择将上述距离测度退化至下列模糊环境下的距离测度进行对比。通过对比,从理论上说明其广泛性与全面性。 1.通过“汽车匀速行驶时,路程随时间的变化”让学生观察和思考:什么在变?什么没变?初步感知“正比例的意义”。 综上,无论是理论方面或者物理意义方面,都说明了广义二重加权距离测度比传统的模糊集距离测度更具有全面性。为了更加突出参数lμ、lπ、lν、lr对最终决策影响的作用。下文默认参数λ的取值为2。 (1)标准化决策矩阵。 (2)计算备选方案的正理想解A+与负理想解A-。 (4)对贴近度进行排序。若Ki越小,则Ai与正理想解的距离越近,即Ai越优。 例1参考文献[17]中的案例,一家跨国公司需要宣布其下一财年的投资政策,有4种方案需要评估。这4种方案中分别对应4个可能的投资地点,即A1巴基斯坦、A2伊朗、A3阿联酋、A4孟加拉国。从舒适区C1、政府法规C2、人民利益C3、市场竞争C44个属性对4个投资方案进行评估。假设所有属性都是有益的,设属性的权重向量ω=[0.22,0.34,0.27,0.17]。政策制定者以IVTSFN的形式提出相关意见,如表1所示。当q=5时,决策矩阵所有值都是IVTSFN;当q<5时,有些值并不是IVTSFN,因此取q=5。 表1 例1中的区间值T-球形模糊决策矩阵(q=5) 通过计算得到正、负理想解A+=([0.8,0.8],[0.0,0.3],[0.5,0.6]),( [0.5,0.7],[0.3,0.6],[0.3,0.3]),([0.7,0.9],[0.3,0.3],[0.1,0.3]),([0.3,0.8],[0.4,0.6],[0.2,0.2]);A-=([0.2,0.2],[0.5,0.5],[0.2,0.6]),( [0.1,0.5],[0.3,0.6],[0.4,0.7]),([0.2,0.7],[0.4,0.4],[0.3,0.5]),([0.3,0.4],[0.4,0.8],[0.4,0.4])。 依据定义的广义二重加权距离测度,选取不同的参数来计算各个方案的贴近度,贴近度越小代表方案距正理想方案距离越小,即代表方案越优,结果如表2所示。由表2可知,对比文献[17]所采用集成算子相关方法评估方案,使用集成算子IVTSFWA得到最终排序结果为A3≻A4≻A2≻A1,利用集成算子IVTSFWG得到最终排序结果为A3≻A2≻A4≻A1。使用这两种集成算子得出的最优方案都是方案A3。与笔者所提算法得到的最优方案绝大部分是一致的,说明了原文方法是有效的。若决策方案对反对意见十分在意时,通过加强非隶属度的权重,如选取参数lμ=0.05、lπ=0.10、lν=0.80、lr=0.05时,结果发生了改变,最优方案变为A4。这说明相比文献[17]的集成算子方法,笔者所提算法能够通过更加灵活的参数选取,得到更多、更全面的符合实际需求的结果。总之,无论是传统的Hamming距离、Euclidean距离或者是集成算子的方法,都未考虑到决策人对获得信息的偏好程度对最终结果所造成的影响。而笔者提出的广义二重距离测度能够适应更多的决策态度,从而得到更加全面的结果。 表2 例1排序结果 具体算法:①通过所定义的广义二重加权距离测度计算每个模式与待识别模式T的距离;②对距离进行排序,距离越小代表模式越相近。 例2假设一家建筑公式需要将一种新型建筑材料T归类到目前已知3种建筑材料Si(i=1,2,3)中去,并根据4种特征Xj(j=1,2,3,4)进行区分,特征权重向量ω=[0.15,0.35,0.40,0.10],对应的模糊决策矩阵如表3所示。当q=3时,决策矩阵所有值都是IVTSFN;当q<3时,有些值并不是IVTSFN,因此取q=3。 表3 例2区间值T-球形模糊决策矩阵(q=3) 选取不同的参数lμ、lπ、lν、lr计算已知材料与未知材料的距离,如表4所示。由表4可知,当考虑第1、2、5种决策情形时,未识别的建筑材料T归类于S3中;而当考虑第3、4两种决策情形时,未识别的建筑材料T则归类于S1。结果对比可以说明,建筑材料T大概率属于S3,小概率属于S1,不属于S2。 (1)基于区间值T-球形模糊集,提出了几种由传统的模糊集距离测度在区间值T-球形模糊集上的扩展,并证明了这几种距离测度满足相关的性质。为了更加符合实际决策态度,提出一种基于区间值T-球形模糊集的广义二重加权距离测度,从理论上说明了相对于传统的距离测度,该方法更具有广泛性与全面性。将这种距离测度应用于解决区间值T-球形模糊集环境的多属性决策方法及模式识别问题,证实了其可行性与有效性。 (2)未来可考虑开发出基于区间值T-球形模糊集的广义二重加权距离测度的属性参数确定方法,并研究IVTSFS的相似性测度、熵测度与偏好关系等问题,然后基于这些研究开发出相关算法用于多属性决策、模式识别、聚类分析等领域。另外,也将考虑IVTSFS与粗糙集理论相结合,探究区间值T-球形模糊粗糙集在粒计算相关领域的基础应用。2 区间值T-球形模糊集距离测度
2.1 区间值T-球形模糊集距离测度
2.2 区间值T-球形模糊集的标准距离测度



2.3 区间值T-球形模糊集的广义加权距离测度


2.4 区间值T-球形模糊集的广义二重加权距离测度
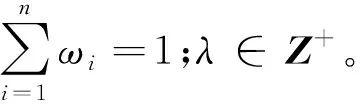

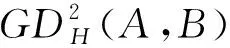
2.5 对比分析

3 应用与实例
3.1 多属性决策




3.2 模式识别


4 结论

