基于五次B 样条的对流-扩散方程数值解法

钱 江，王永杰

（河海大学 理学院，江苏 南京 211100）

1975 年,王仁宏教授利用函数论与代数几何的方法开创性地建立了任意剖分下多元样条函数的理论框架,提出了研究多元样条最一般的方法,即光滑余因子协调法[1-3],并由此，取得了丰硕的多元样条理论与应用研究成果。具体而言,利用光滑余因子协调法可以计算出2 型三角剖分上的二元三次样条基函数[4]；进一步,利用保多项式性,构造出基于线性泛函的样条拟插值算子[5]，推导出样条拟插值的导数逼近方法[6]。此外,多元样条在其他领域也获得了不错的成果。文献[7]利用三次样条方法给出了Poisson 方程的数值求解。文献[8]建立了三次样条函数与导数的计算公式,并应用于求解对流扩散问题。文献[9]提出了一种样条运动方法,将四次样条曲线表示物体的外部轮廓,从而探索基于图像的IBVS 的轮廓跟踪任务。白根柱[10]构造了一段特定条件下的三次有理B 样条曲线,即曲线通过给定的控制多边形始末端点,且与始末控制多边形相切,后以该曲线为轴线的管道光滑拼接出轴线异面管道。王慧等人[11]为了高效地获得拟合曲线,在均匀三次B 样条曲线的基础上,提出一种双层最小二乘渐进迭代逼近算法。文献[12]在混合B 样条的基础上构造新的技术,给出一种非结构化样条实体等几何拓扑优化方法。沈菀蔷等人[13]在B 样条基础上给出一种变次数样条曲线的细分算法,该算法可在细分前指定每段的次数和两段曲线之间的连续性。文献[14]为了提高三维模型之间拼接曲面的精度和效率,提出一种基于三次均匀B 样条曲线曲面的网格融合方法。文献[15]为了证明半离散格式解的有界性与收敛性,用三次B样条有限元法给出一类四阶主项带有变系数的抛物方程。文献[16]为了获得的平滑航迹整体过渡自然,采用B 样条曲线插补法求解航迹的平滑问题。齐远节等[17]提出了两种新的求解对流扩散方程的三次样条差分格式。王森[18]把牛顿插值公式拓展到埃尔米特插值公式和样条函数插值的使用领域，给出了解决插值问题简便高效的方法。

考虑到更高次的样条函数在逼近理论中应具有更高的精度[19],而计算高次的B 样条需要较复杂的方法与技巧,由此将高次样条函数应用于微分方程数值解值得进一步研究。作者拟考虑建立五次B 样条方法,同时注意到在比较五次B 样条微分正交法时发现,文章[20]仅仅给出无重节点情况下的五次B 样条函数,且该函数并不具有单位分解性，在逼近曲线的过程中优势不明显。而利用de Boor-Cox 公式计算均匀节点下的五次B 样条需要558 次运算,同时计算带有重节点的五次B样条运算步骤更多,更加繁琐。在多种情况考虑下,本文将利用光滑余因子协调法,从最小支集的角度计算在均匀剖分下的五次B 样条基函数[21],并将其运用在求解一类对流扩散方程中。

1 均匀五次B 样条基函数的计算

首先给出光滑余因子协调法[1-3]的定理作为计算五次B 样条基函数的准备工作。

定理 1设一个一元 n 次样条s(x)∈S(x0,x1,x2,…,xN) 的互异节点为{x0,x1,…,xN},且具有局部支集(x0,xN),则此样条函数可表示为

利用定理1,可以计算出任意次均匀B 样条基函数,拟将样条逼近方法应用于微分方程数值解,本文将给出在均匀节点上不同情况下的五次B 样条基函数,尝试得到运用五次样条基函数拟合对流-扩散方程的方法。

再利用B 样条基函数的单位分解性可得

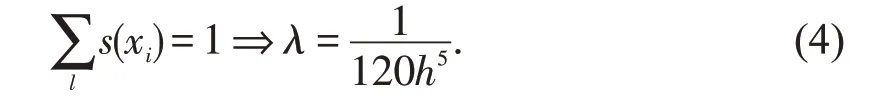
这样,给出了步长为h,均匀节点为{xi,xi+1,xi+2,xi+3,xi+4,xi+5,xi+6} 的五次B 样条函数,即

且在子区间Ii:=[xi,xi+1] 中存在唯一一组五次B 样条基函数

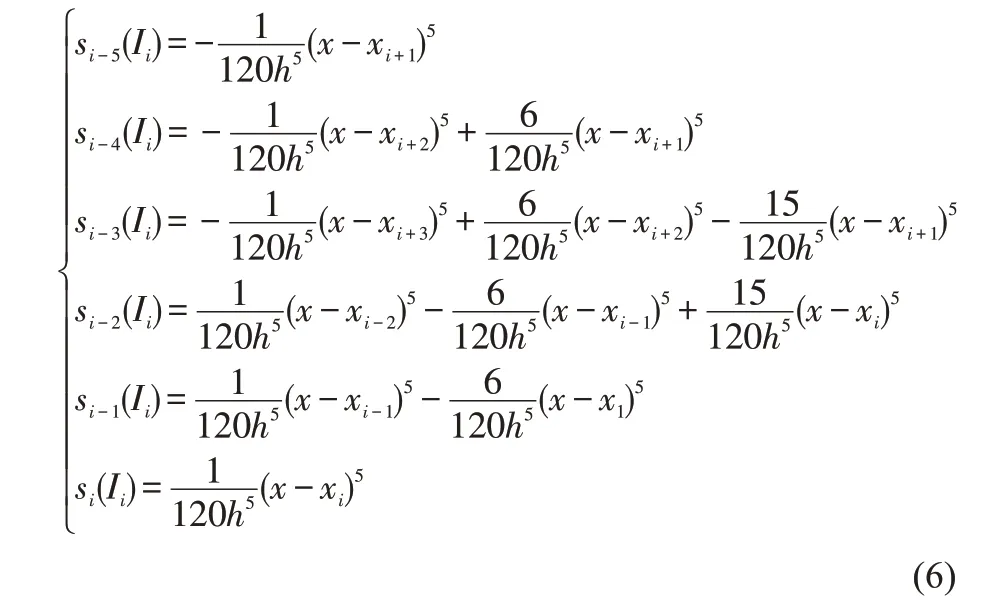
如图1 所示,通过光滑余因子协调法[2-4]得到的均匀五次B 样条基函数具有非负性、单位分解性等优秀的性质。

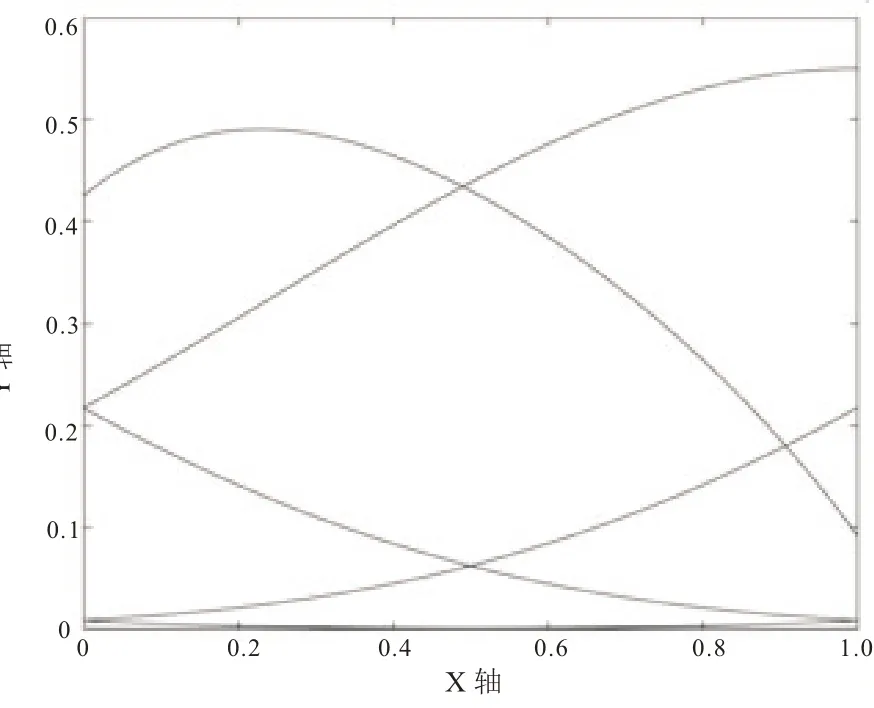
图1 均匀五次B 样条基函数

2 区间端点带重节点的样条基函数

考虑在有界闭区间[x0,xn] 内均匀步长为h,将得到在x0,xn处具有不同个数重节点的五次B 样条的具体表示,从而得到每个支集上的五次样条函数。

情形1.考虑x-1=x0＜x1＜x2＜x3＜x4＜x5,设在节点x-1=x0,x1,x2,x3,x4,x5处的光滑余因子分别为。可得协调方程为

同理可得在节点为x-2=x-1=x0＜x1＜x2＜x3＜x4时的五次B 样条函数为

情形4.在x-4=x-3=x-2=x-1=x0＜x1＜x2的情况下,我们设节点x-4=x-3=x-2=x-1=x0,x1,x2的光滑余因子为

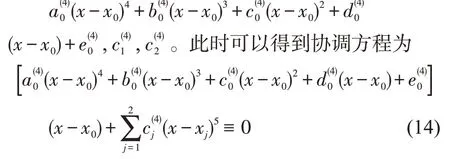
同理,在节点为x-4=x-3=x-2=x-1=x0＜x1＜x2时的五次B 样条函数为

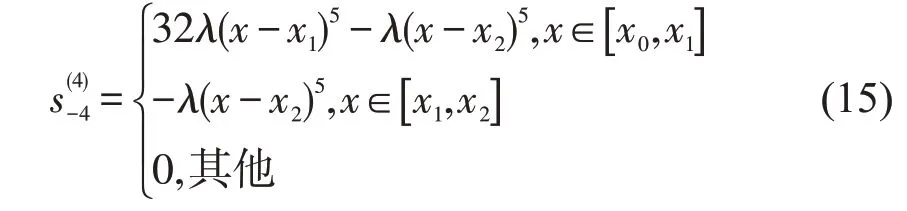
情形5.当x-5=x-4=x-3=x-2=x-1=x0＜x1时,我们设节点x-4=x-3=x-2=x-1=x0,x1处的光滑余因子分别为

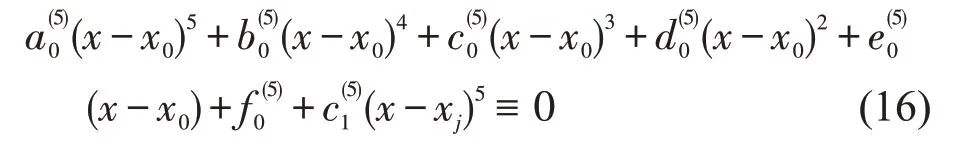
同理可得节点为x-5=x-4=x-3=x-2=x-1=x0＜x1时的五次B 样条函数为

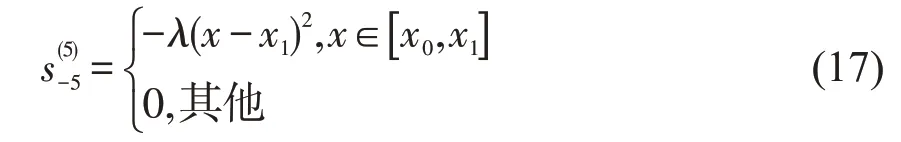
定理 2设节点为x-5=x-4=x-3=x-2=x-1=x0＜x1＜x2＜x3＜x4＜x5＜x6且xi+1-xi=h,i=0,1,…,5 时,在每个子区间内存在唯一一组五次B样条基函数,分别为

在I0=[x0,x1] 上,基函数为

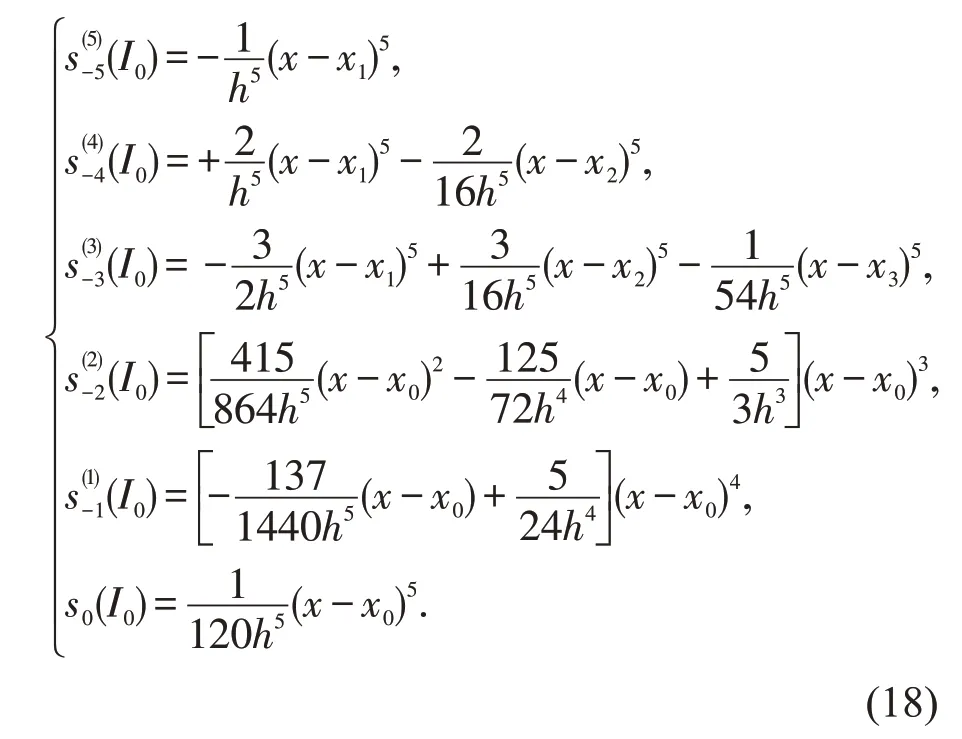
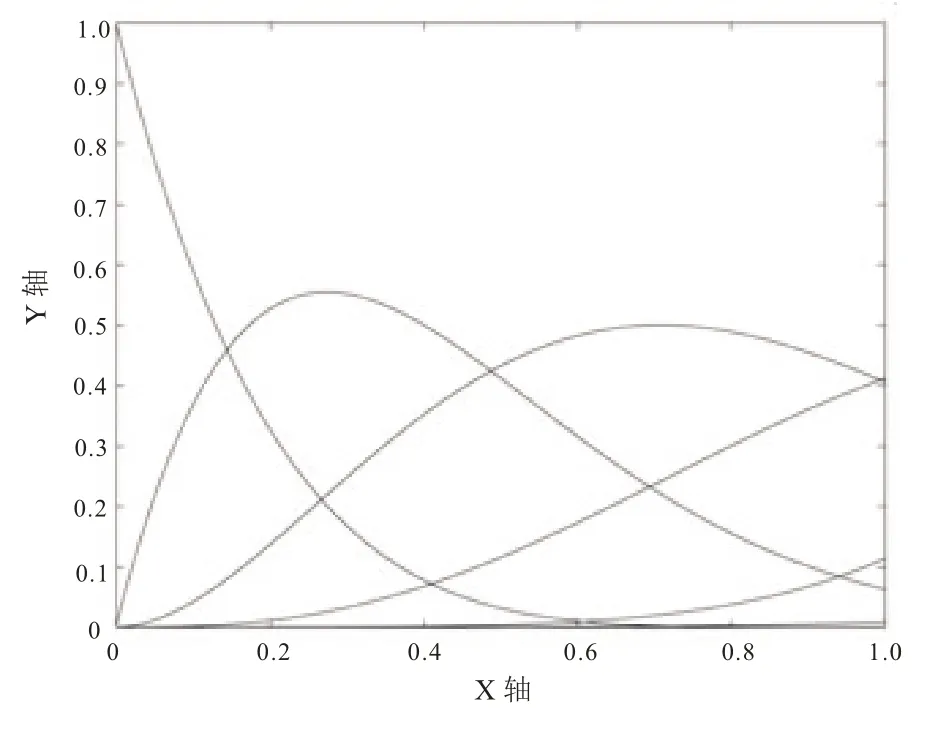
图2 I0=[x 0,x1] 上的五次B 样条基函数图像

在I1=[x1,x2] 上,基函数为

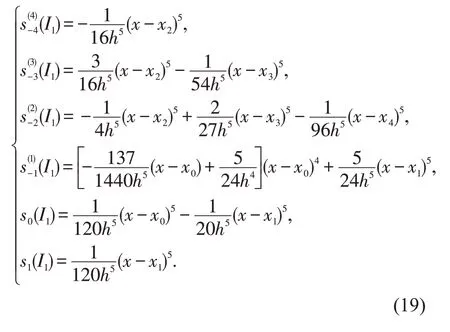
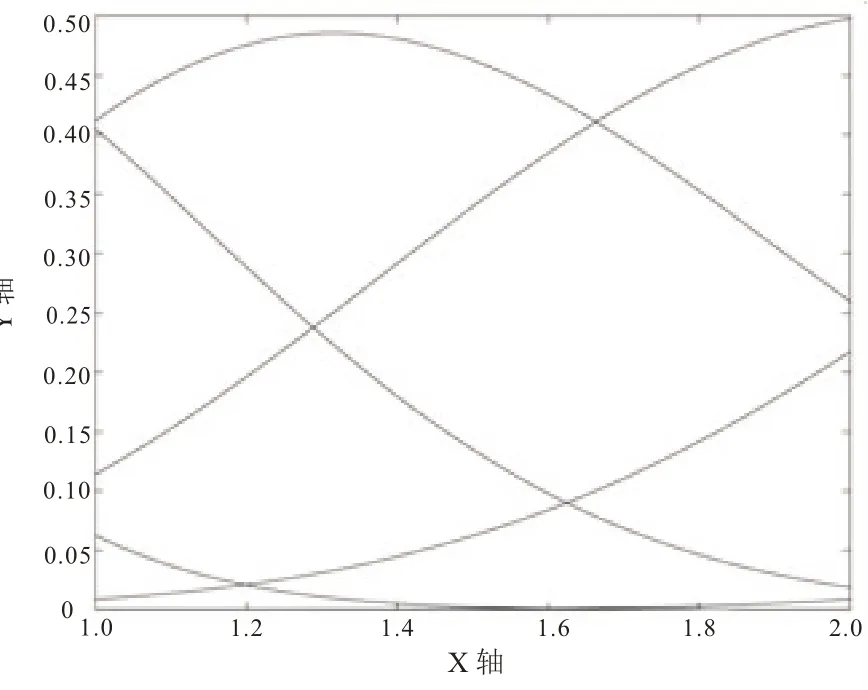
图3 I1=[x1,x2]上的五次B 样条基函数图像

在I2=[x2,x3]上,基函数为

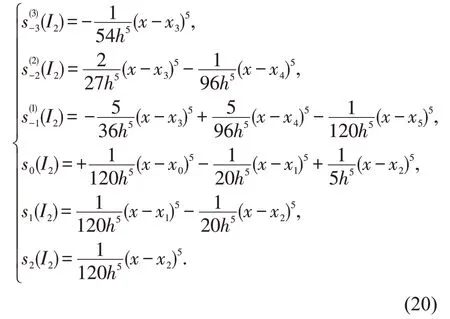
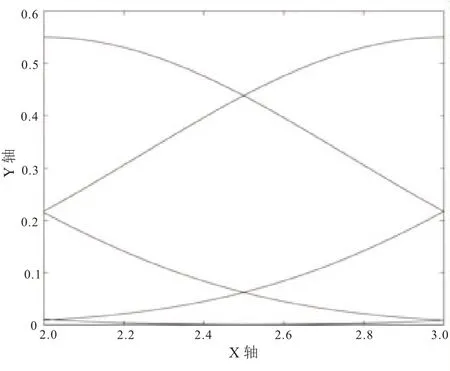
图4 I2=[x2,x3]上的五次B 样条基函数图像

在I3=[x3,x4]上,基函数为

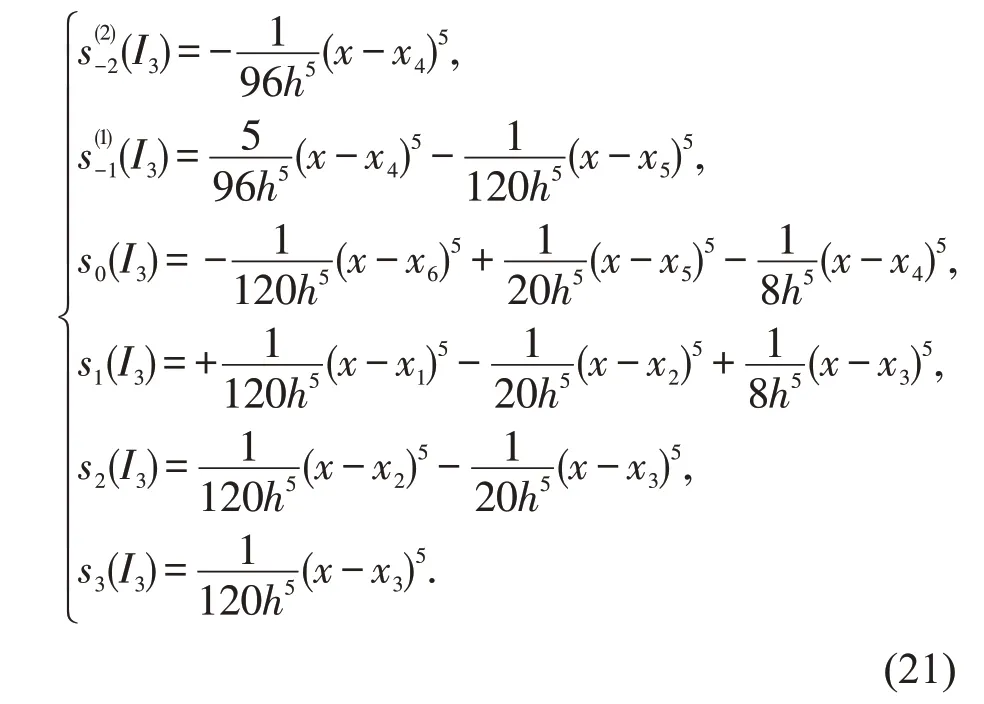
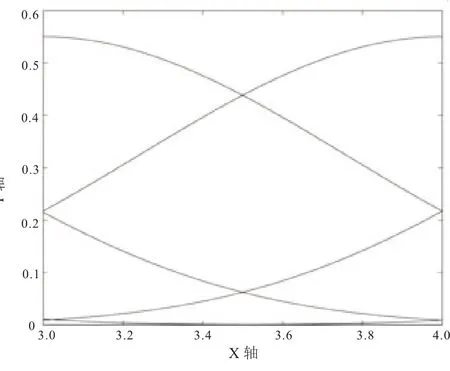
图5 I3=[x3,x4]上的五次B 样条基函数图像

在I4=[x4,x5]上,基函数为

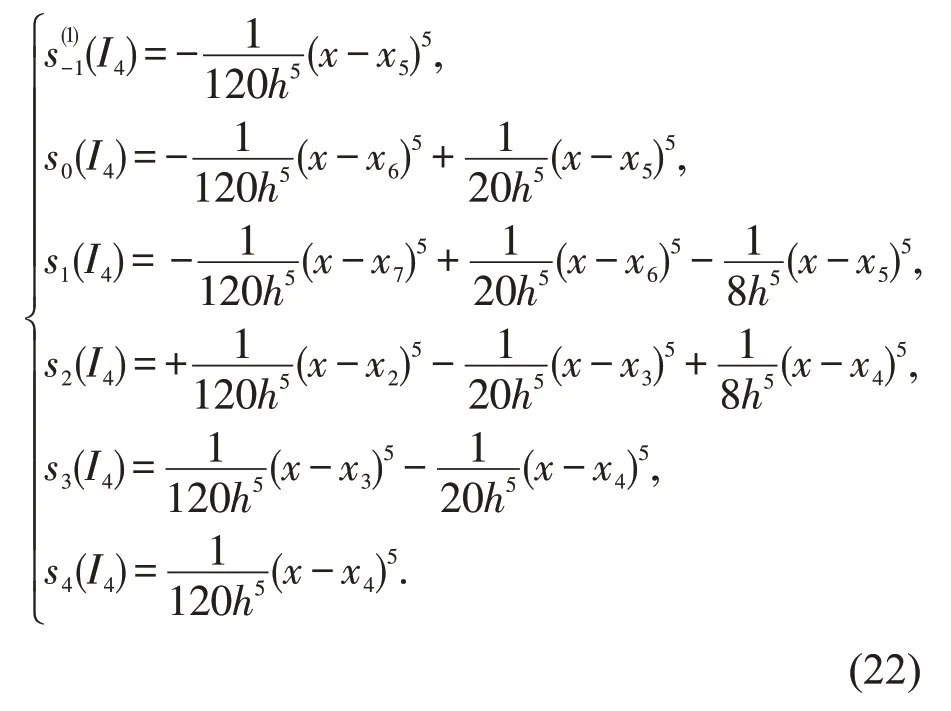
图6 I4=[x4,x5]上的五次B 样条基函数图像

证明在单区间I0=[x0,x1]内存在的B 样条函数有

由B 样条基函数的单位分解性知

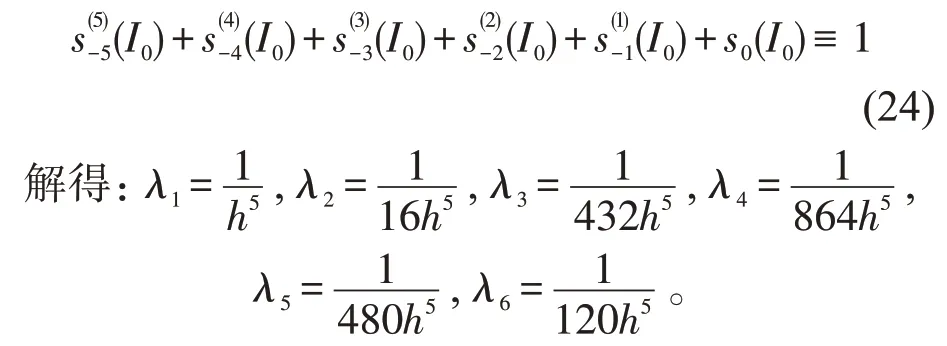
由此得到式(18)。同理可证得式(19),(20),(21),(22)。

证毕

类似于对左端点处带重节点的五次B 样条的分析,同样可以得到右端点处带重节点的五次B样条的结论。

定 理 3设xn-6＜xn-5＜xn-4＜xn-3＜xn-2＜xn-1＜xn=xn+1=xn+2=xn+3=xn+4=xn+5且xi+1-xi=h,i=n-6,n-5,…,n-1,则在每个子区间内存在唯一一组的五次B 样条基函数,即在In-1=[xn-1,xn]上,基函数为

证明在单区间In-1=[xn-1,xn]内存在的B 样条函数有

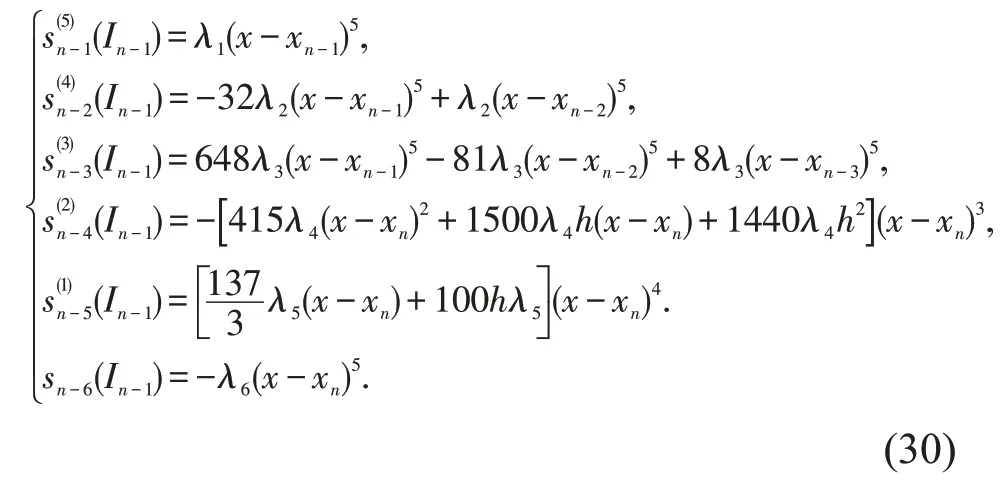
由B 样条基函数的单位分解性知

3 对流-扩散方程的样条逼近格式

令u(x,t)为如下初边值问题的真解[22]：

其中,u为在时刻T点x处的体积浓度,v是对流速度,Dx为扩散系数。

对方程(32)在点(xi,tk)按时间步长进行离散,引入参数δ(0 ≤δ≤1),我们得到

其中,是u(x,t)在点(xi,tk),xi=ih,tk=kτ处的逼近解。h=1∕I,τ=T∕M,I＞1 和K＞1 是两个整数。

接下来,利用均匀节点下的五次B 样条基函数来拟合对流-扩散方程。记点()xi,tk处的逼近解为

首先给出均匀节点下的五次B 样条函数si(x)及其导数在各节点处的值,如表1。

表1 及其导数在各节点处的值

根据表1 可知,逼近解及其关于x的一阶和二阶导函数分别为

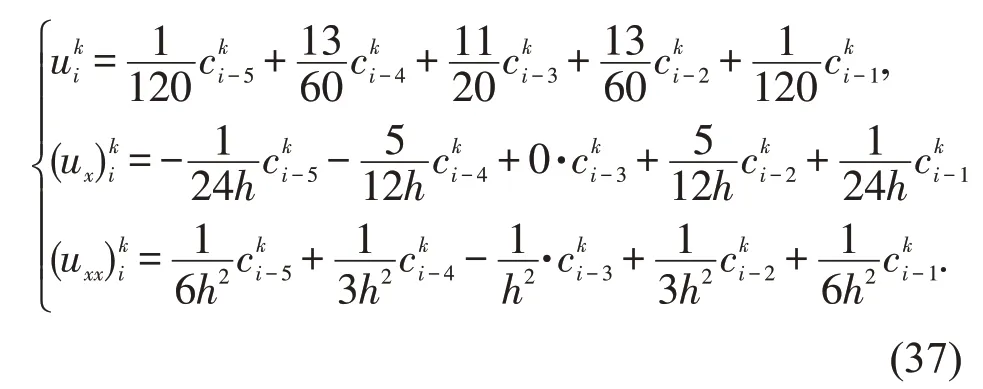
将式(37)代入式(35)中,生成具有n+5 个未知量的n+1 个方程。为了使方程组具有唯一解,还需要另外添加4 个方程。由边界条件可得

n+5 个方程组的矩阵矩阵表示为

其中,P,R∈R(n+5)×(n+5);Ck+1,Ck,b∈R(n+5),

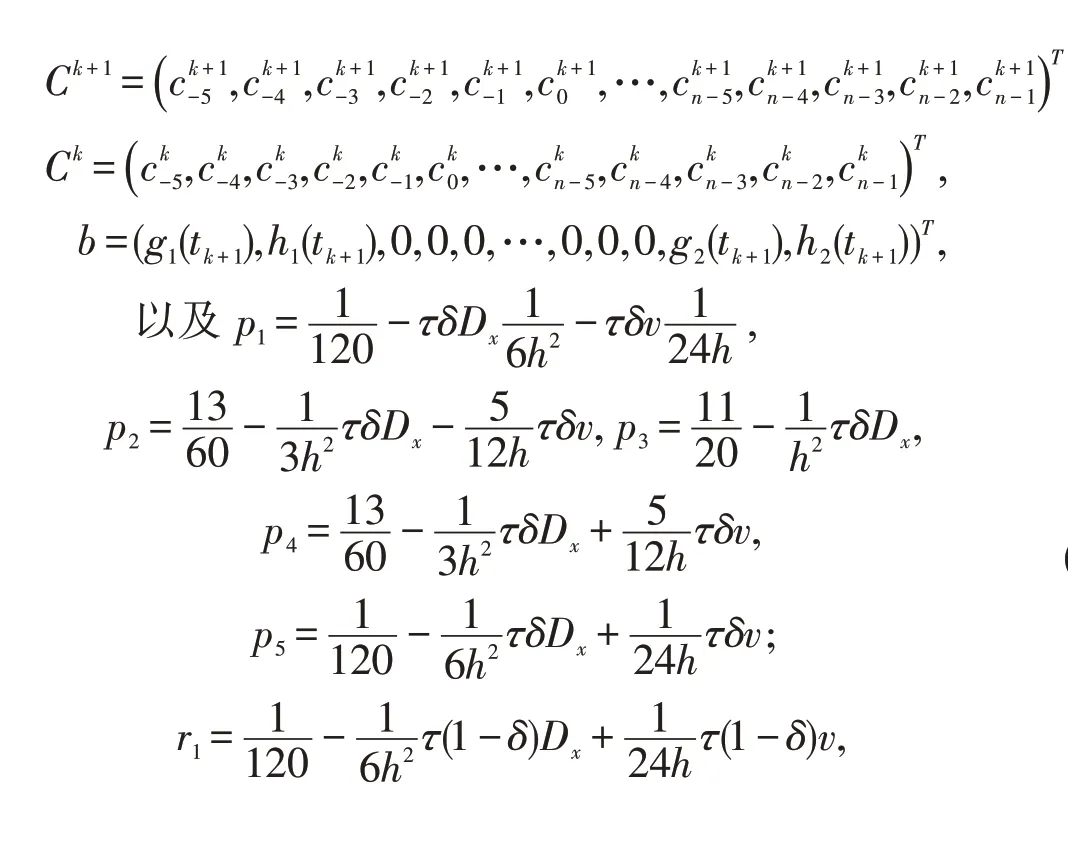
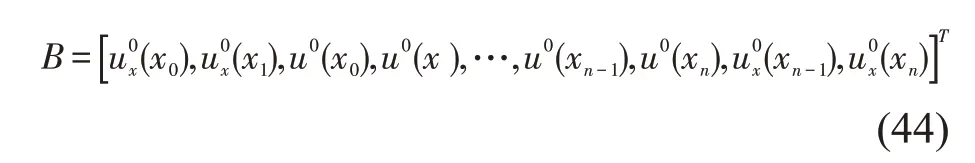
求出C0则第k+1 时间层的逼近解就可由(39)式计算得到。

4 数值算例

考虑模型问题(32)-(34),选择精确解为

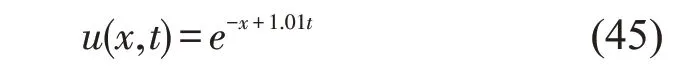
其中x∈[0,1],t∈[0,1]。相应的初边值可以由它得到。

选择用五次B 样条基函数逼近该模型。取时间步长τ=0.04,空间步长h=0.02,δ=0.5。在表2 中,我们取t=0.2,对取不同值与精确解作对比。

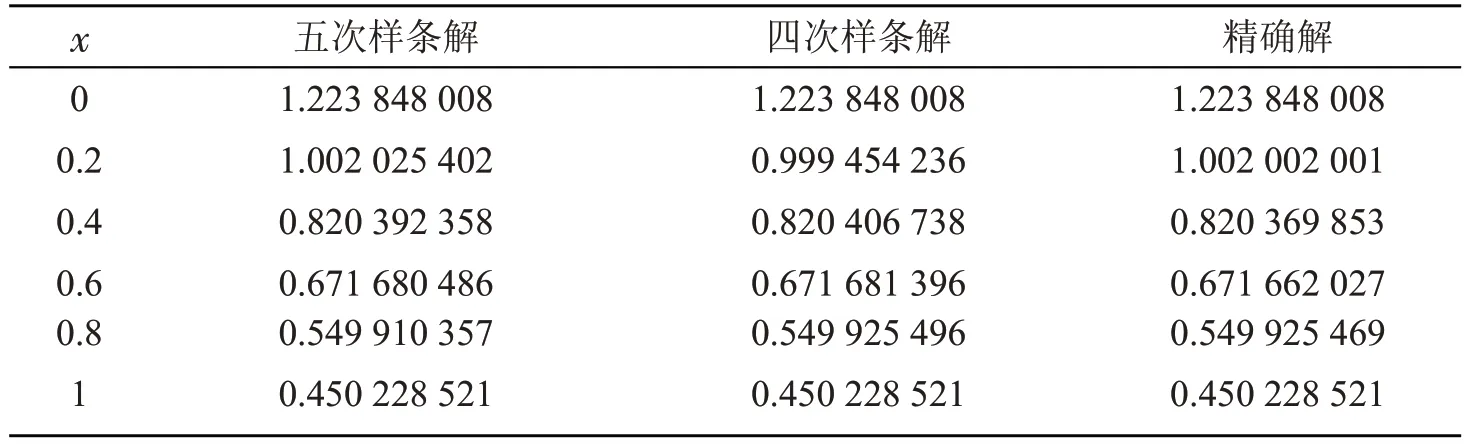
表2 五次样条解、四次样条解与精确解对比

表3 为表2 的两种方法得到的解与精确解的数值误差对比。

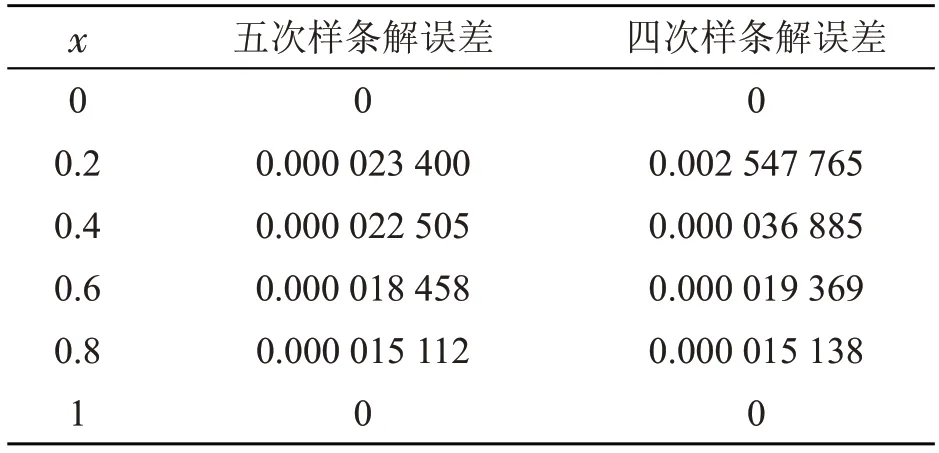
表3 与精确解的数值误差对比

从表2 和表3 可以看到,用五次B 样条逼近得到的解准确率高,而且得到的解与精确解的误差远小于比它低一次的四次B 样条解误差,逼近效果更好。用对流-扩散方程举例,虽然常用三次样条逼近,但在相同步长的情况下,在相同的有限闭区间上需要更少的五次B 样条，取得更好的逼近效果。

需要指出的是,为了更好地分析五次样条的逼近效果,首先需要建立具有保高次多项式性的五次样条拟插值算子,这样可以建立样条解与精确解之间的误差分析,目前由于这方面工作计算量很大，主要限于三次样条情形。限于篇幅,只计算出满足单位分解性,即保常数的五次B 样条(包括均匀节点与带重节点切线),再结合样条的分段光滑性配置系数,从而递推计算出这些系数,避免了Gauss 消去法求解线性方程组的繁琐过程(注：递推计算复杂度往往是ο(n2),而消去法计算复杂度是ο(n3),与差分法的不连续性。数值算例也表明,采用五次B 样条计算出的数值解逼近效果优于采用四次B 样条的计算结果。另外,本文所提的五次B 样条递推算法不仅应用于求解对流-扩散方程,而且适用于一般的线性双曲型方程或方程组。

5 结语

由于所采用的的五次样条函数具有非负性与单位分解性,因此具有稳定的求解过程,精度高于基于三次和四次样条函数得到的结果,并且用光滑余因子协调法计算出的样条函数在区间端点处的连接处光滑性更高。限于篇幅,后续将进一步研究基于五次B 样条的样条拟插值算子,将其应用于求解偏微分方程,从理论上分析五次样条求解微分方程的稳定性与收敛性。

在以后的工作中,作者将建立保高次多项式性的五次样条拟插值算子,并分析逼近误差,将其应用于求解微分方程或方程组。