几类广义Pexider方程的解
肖志涛
(广州华立学院, 广东 广州 511325)
Pexider方程是Pexider J V在文献[1]中提出的一组方程,形式如下:
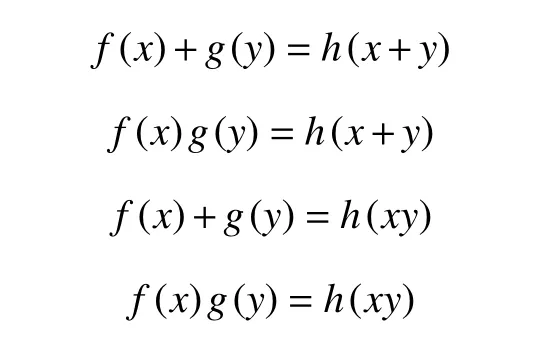
并给出了方程在实数域 R上的连续解。一直以来,很多人致力于这组方程的研究,得到了许多有意义的成果,文献[2-7]研究了Pexider方程在不同区域上解的情况,文献[8-9]讨论了可加Pexider方程在集值函数空间的稳定性,文献[10-14]讨论了几类Pexider方程和时滞方程在不同赋范空间上的解及稳定性。本文研究如下形式的广义Pexider方程:
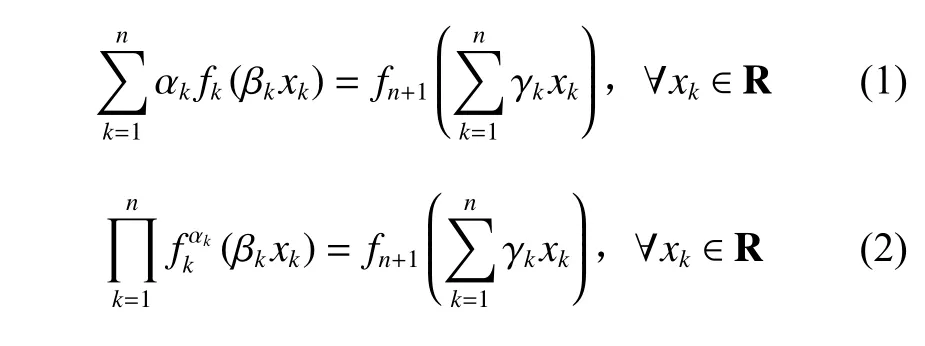
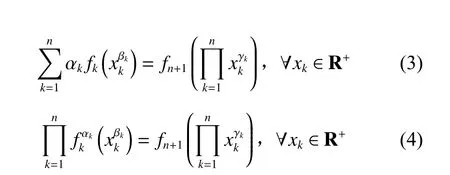
其中 αk,βk,γk为常数,且αkβkγk≠0,(n≥2)。通过赋值转化方法,得到了上述方程的通解。
1 引理及基本准备
首先,本文给出下面的引理[15-16]:
引理1设f是定义在 R 上的连续函数,如下几个方程
f(x)+f(y)=f(x+y),∀x,y∈R
f(x)f(y)=f(x+y),∀x,y∈R
f(x)+f(y)=f(xy),∀x,y∈R+
f(x)f(y)=f(xy),∀x,y∈R+
在不考虑平凡解f≡0的情况下,分别有解为
f(x)=f(1)x,(x∈R)
f(x)=ecx=ax,(c为任意常数,x∈R)
f(x)=clnx,(c为任意常数,x∈R+)
f(x)=xc,(c为任意常数,x∈R+)
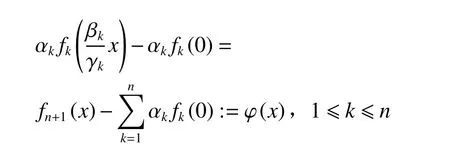
下面,将引理1推广为一般的形式,有
引理2设f是定义在R 上的连续函数,如下几个方程
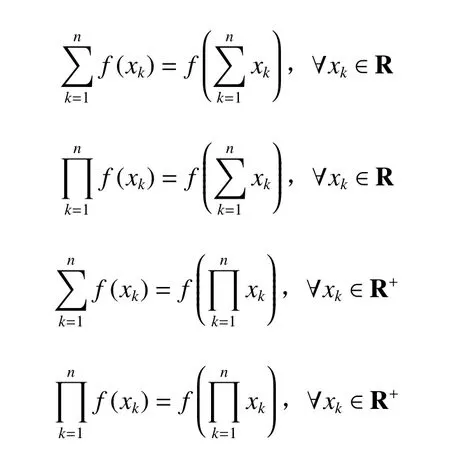
在不考虑平凡解f≡0的情况下,分别有解为
f(x)=f(1)x,(x∈R)
从而有
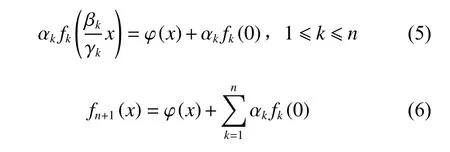
于是,有
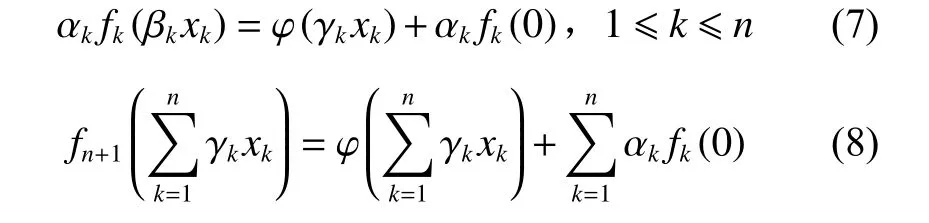
将式(7)、(8)代入方程(1),整理可得
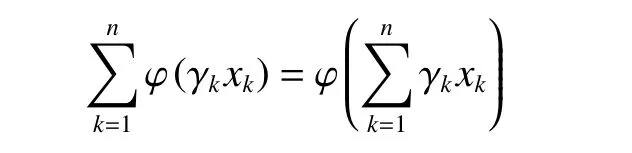
由引理2可得
φ(x)=φ(1)x
f(x)=ecx=ax,(c为任意常数,x∈R)
f(x)=clnx,(c为任意常数,x∈R+)
f(x)=xc,(c为任意常数,x∈R+)
证明由引理1可得结论成立。
由式(5)、(6)可得
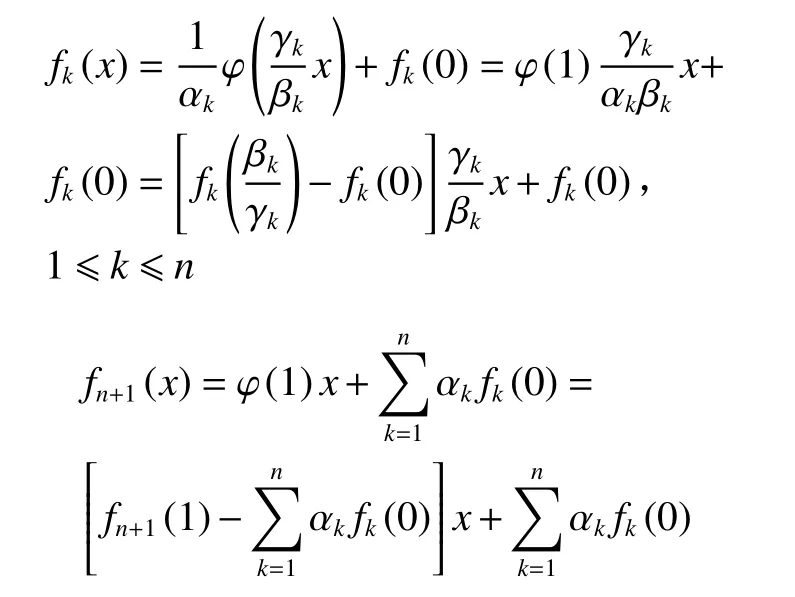
2 主要结论及证明
定理1设fk(1 ≤k≤n+1,n≥2) 是定义在R 上的连续函数,广义Pexider可加方程(1)在不考虑平凡解fk≡0(1 ≤k≤n+1,n≥2)的情况下,有解为
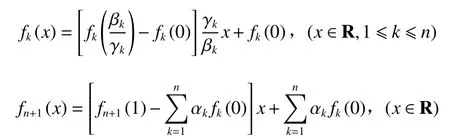
证明在方程(1)中,固定某个xk=x,令其他n−1个xk=0,有
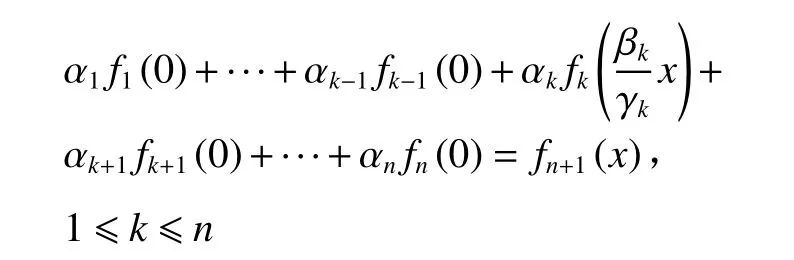
定理2设fk(1 ≤k≤n+1,n≥2) 是定义在 R上的连续函数,广义Pexider指数方程(2)在不考虑平凡解fk≡0(1 ≤k≤n+1,n≥2)的情况下,有解为
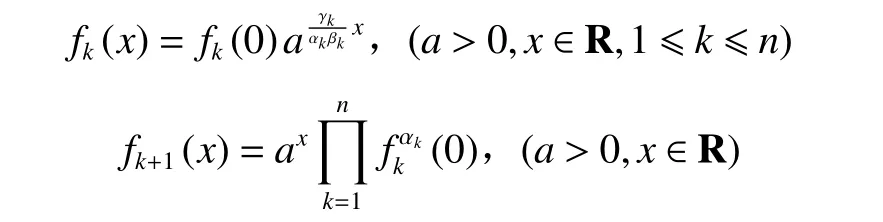
证明由于不考虑平凡解,在方程(2)中固定某个xk=x, 令其他n−1个xk=0,有
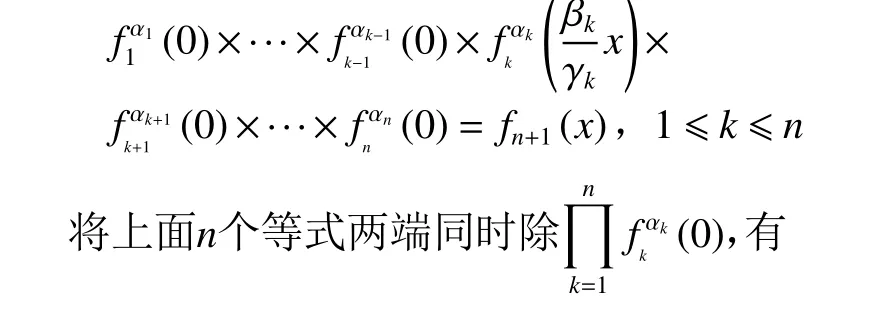

从而
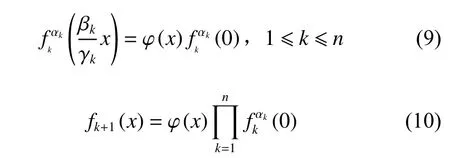
于是
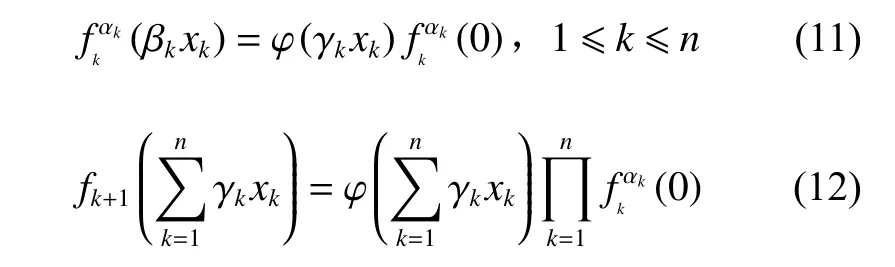
将式(11)、(12)代入方程(2),整理可得
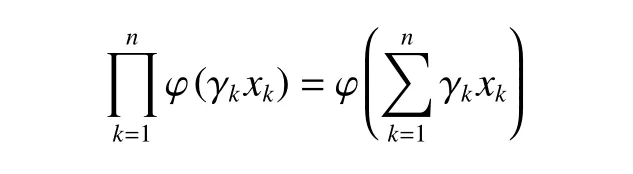
由引理2可得,上式有解
φ(x)=ecx=ax,(a>0)
由式(9)、(10)可得
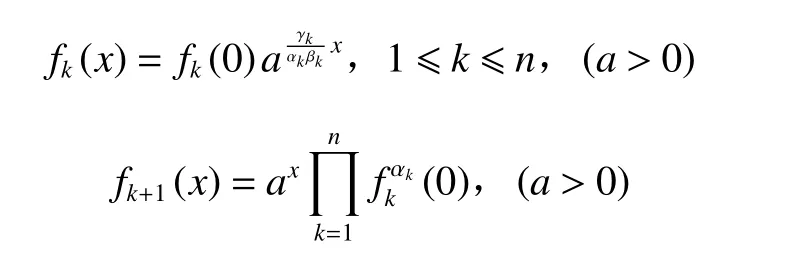
定理3设fk(1 ≤k≤n+1,n≥2) 是定义 R+上的连续函数,广义Pexider对数方程(3)在不考虑平凡解fk≡0(1 ≤k≤n+1,n≥2)的情况下,有解为
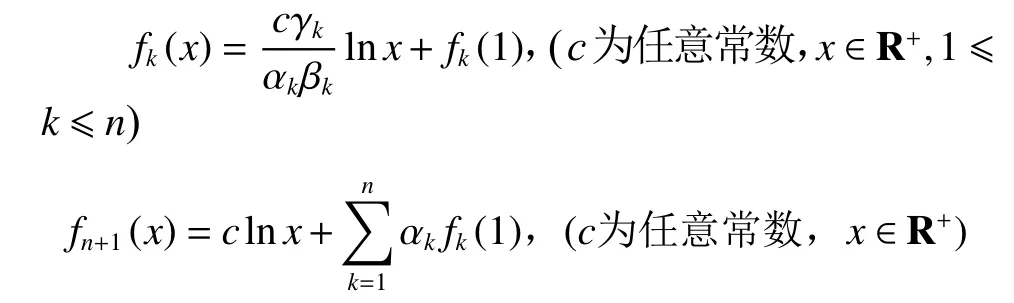
证明在方程(3)中固定某个xk=,令其他n−1个xk=1,有
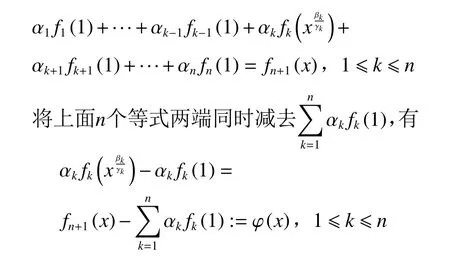
从而有
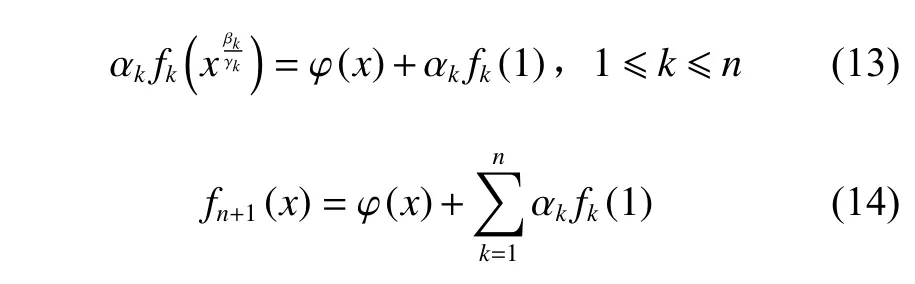
于是,有
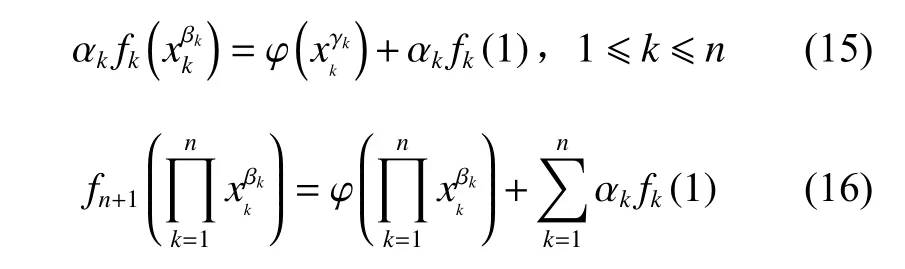
将式(15)、(16)代入方程(3),整理可得
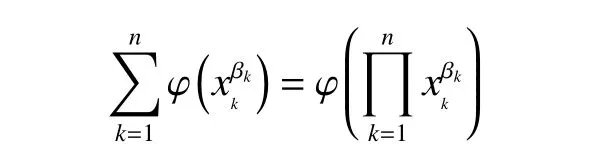
由引理2可得
φ(x)=clnx
由式(13)、(14)可得
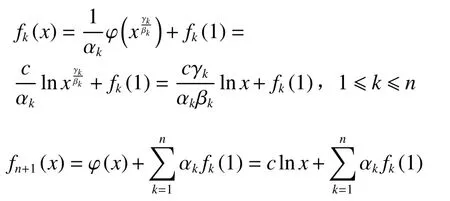
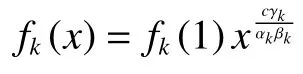
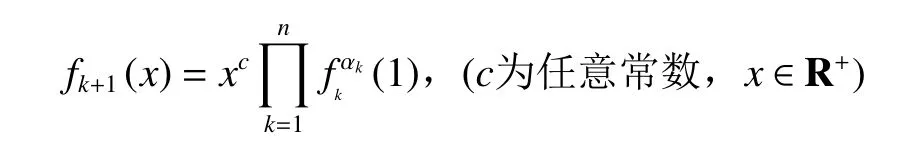
证明由于不考虑平凡解,在方程(4)中固定某个xk=,令其他n−1个xk=1,有
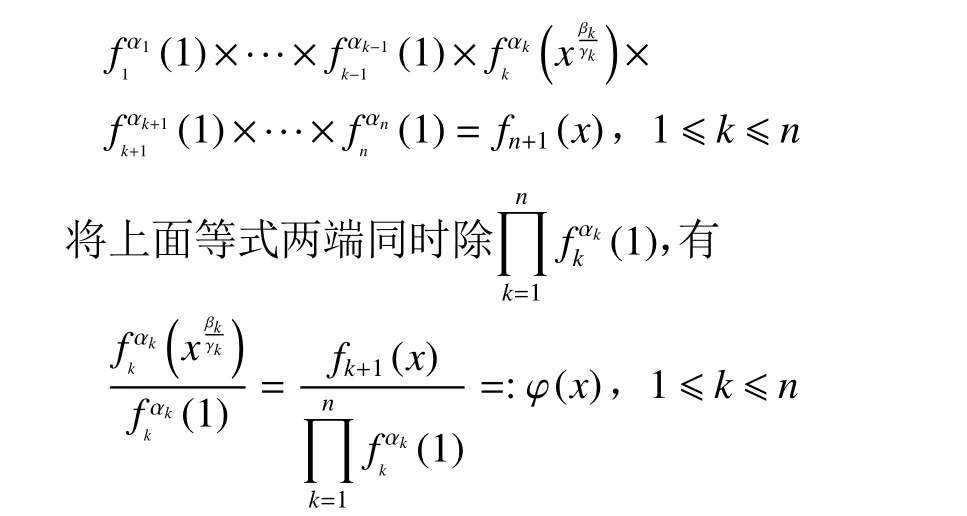
从而
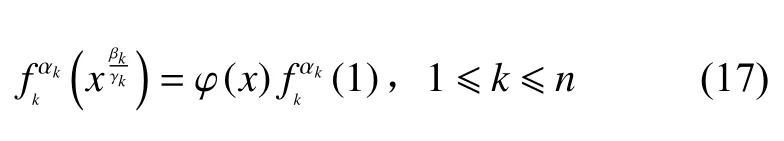
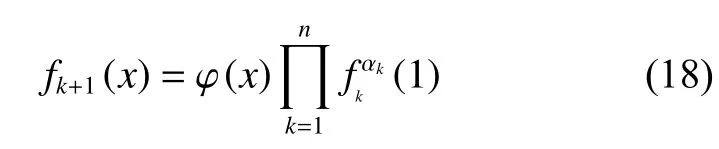
于是
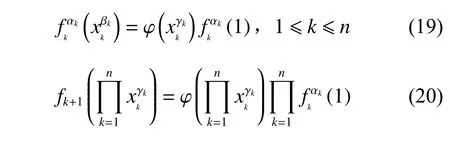
将式(19)、(20)代入方程(4),整理可得
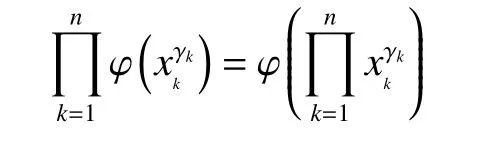
由引理2可得,上式有解
φ(x)=xc,(c∈R)
由式(17)、(18)可得