基于随机素描方法的在线核回归

刘清华，廖士中

（天津大学智能与计算学部，天津 300350）

0 引言

在线核学习需要在后悔界和计算复杂度之间做出权衡，具体是指在线学习算法在降低计算复杂度的同时，必须保证一个关于回合数T的亚线性后悔界。在线线性学习中，在线梯度下降（Online Gradient Descent，OGD）是高效且通用的算法，但可能会遭遇“核化诅咒”（Curse of Kernelization）［1-4］。随着回合数T的增加，核矩阵的规模也会逐渐增大，使得处理核矩阵的时间会大幅增加，从而导致计算复杂度提高。

在线核学习中有多种方法用于避免核化诅咒的发生。

有些方法是基于对支持向量（Support Vector，SV）的维护：预算维护策略的主要思想是维护一个规模有限的支持向量集合，每回合的计算复杂度至多是支持向量集的规模的多项式级；随机预算感知机（Randomized Budget Perceptron，RBP）［5］、Forgetron［6］、预算在线梯度下降（Budget Online Gradient Descent，BOGD）以及预算感知机［7］都是遵循不同的策略，在每回合舍弃一些支持向量。除此之外，很多方法还会通过对支持向量的投影或归并操作来维护支持向量集。

有些方法基于核函数近似技术，比如傅里叶在线梯度下降（Fourier Online Gradient Descent，FOGD）和Nyström 在线梯度下降（Nyström Online Gradient Descent，NOGD）［8］。NOGD应用Nyström 方法近似核矩阵，然后再应用在线梯度下降方法进行学习。相关文献已经证得NOGD 是一个通用框架，且在所有现存方法中有相当可观的性能表现。

跟导（Follow-The-Leader，FTL）［9］方法是在线凸优化中一个很重要的思想，该方法考虑所有过往的回合来获得当前的假设，具体来说，当前假设应使得过往所有回合的累计损失最小。首先用Nyström 方法近似核矩阵，然后提出一个新颖的梯度下降方法用于后续的学习。参考FTL 的思想，在第t回合中，使用前t-1 回合的累计损失的平均梯度来做梯度下降，将这种方法称为跟导在线核回归（FTL-Online Kernel Regression，F-OKR）。后面会给出该方法的亚线性后悔界。

为了给F-OKR 方法加速，选择应用素描方法嵌入其中，素描技术广泛应用于流数据学习的领域［10-15］。Ye 等［16］提出了一种基于素描技术的方法来近似矩阵乘法，用于在线典型相关性分析（Canonical Correlation Analysis，CCA），并且证明了该方法的空间复杂度比现存其他CCA 方法都低；文献［17］中提出了应用高斯随机投影、频繁方向（Frequent Directions，FD）、Oja 素描来近似二阶在线学习中高计算复杂度的海森阵（Hessian），并提出了素描在线牛顿法（Sketched Online Newton，SON），该方法的时间复杂度是关于特征维度线性的，同时后悔界为亚线性的；张骁等［18］应用随机素描技术构造假设空间素描，在此基础上研究在线模型选择，给出系统的在线核选择理论，设计了在线核选择准则及高效的在线核选择算法，但该项工作针对的是在线核选择中的问题，而下文所针对的是在线回归学习提出了学习算法，并应用矩阵素描技术进行算法计算复杂度的优化。

特殊地，应用FD 方法来计算累计损失的梯度，将这种修改后的版本称为素描在线核回归（Sketched Online Kernel Regression，SOKR）。实验表明F-OKR 和SOKR 的回归精确度比NOGD 高，且SOKR 的运行时间显著小于F-OKR。

1 预备知识

1.1 符号表示

用大写加粗的字母（如A）表示矩阵，小写加粗字母（如a）表示向量，不加粗字母（如a或B）表示标量。矩阵A的第i行表示为[A]i；用It∈Rt×t表示t维的单位矩阵；A≥B表示A-B是一个半正定矩阵；用‖ ‖⋅表示向量的ℓ2范数和矩阵的谱范数；‖ ⋅‖F表示矩阵的F 范数；令[T]表示集合｛1，2，…，T｝。

给定一个正定核函数κ：X× X→R，其中X表示一个任意的输入空间。与κ相关的再生核希尔伯特空间表示为H，可得相关的特征映射为ϕ：X→H，则κ(x，x′)表示一个内积。一般情况下，特征映射ϕ的具体形式难以得知，通常使用这样的内积形式来隐式地表达这个映射及特征空间，且对任意函数fw∈H，可以将其表示为映射值和权重w相乘的形式，即fw=ϕ(x)Tw。定义权重假设第t回合的可行集为且。

在线核学习中，第t回合的核矩阵可写为一个协方差矩阵的形式，其中定义特征矩阵为Φt=。

1.2 跟导方法

在线凸优化是一个很重要的学习模型。以在线凸优化为问题背景，在当前回合，选择最小化过往回合累计损失的向量，这个思想称为跟导方法[9]。在第t回合，目标函数为：

令损失函数ℓ 为平方损失。

FTL 的在线二次优化可以导出O(lbT)的后悔界，其中T为总回合数。

1.3 Nyström在线梯度下降

Nyström 在线梯度下降是一个大规模在线核学习的框架，其基本思想是通过函数化近似技术近似核函数，该方案可以表示为两个阶段。在早期学习阶段，当支持向量的数量小于b时，应用任意在线学习方法（如在线梯度下降）即可，其中b是算法里提前定义的预算。一旦支持向量的数量达到了预算值，再接收到新样本时，将会用当前的支持向量集近似其核映射值，这意味着将用核矩阵的一部分列来近似整个核矩阵。这个思想简化了第二阶段的计算，即不用再考虑用一些策略维护支持向量集，而是直接固定支持向量集；所以在线核学习中，NOGD 比其他方法更高效、可扩展。

参考NOGD 的框架，本文选用Nyström 近似方法［19-20］近似核矩阵。在大规模在线核学习中，Nyström 方法广泛应用于批处理核矩阵近似方法，且有后悔界的理论结果。

1.4 频繁方向

近些年，大规模矩阵的近似问题在大规模机器学习中越来越受重视，其中频繁方向算法由于其逐行处理矩阵的特点，与在线学习很契合。本文应用频繁方向算法[21]来获得一个高效的协方差矩阵的近似，这样的近似矩阵具有与原矩阵相同的规模，但同时会大幅减小计算量。

接下来简单描述FD 算法（详见算法1）。给定一个矩阵A∈Rn×d，FD算法会输出A的一个素描矩阵，表示为B∈Rc×d，其中c≪n。这个素描矩阵将会一直保持c×d的规模，每当新的一行到达时，矩阵内容都会更新，新到达的一行插入矩阵B的第c行，也就是最后 1 行。[U，Σ，V]←SVD(B)表示对矩阵B的奇异值分解（Singular Value Decomposition，SVD）。算法第4）、5）行会保证矩阵B的最后1 行一直为全零行。由于UTU=VTV=Ic，所以在算法中有。这一步骤不仅对于BTB的值没有影响，还可以简化得到B及BTB的计算量。

具体地，本文需要将矩阵Φ进行转置来适应FD 算法。对于任意数据矩阵Φ=[ϕ(x1)，ϕ(x2)，…，ϕ(xT)]∈Rd×T，则Φ的协方差矩阵为ΦΦT∈Rd×d。

应用素描矩阵近似该协方差矩阵得：

其中C∈Rd×c，c≪T。

算法1 FD 算法。

输入c，A∈Rn×d，B∈Rc×d为一个全零矩阵。

输出。

2 素描在线核学习

本章将给出跟导在线核学习方法及一个用素描方法加速的版本。首先，应用Nyström 方法近似核；然后，通过跟导在线核回归算法更新假设。

2.1 跟导在线核回归

参考FTL 的思想，在线核学习在第t回合的目标函数可写作：

然后选用梯度下降方法求解该函数，其中用到的是前t-1 回合的累计损失的平均梯度。设定ℓ 为平方损失，则该梯度为：

在第t回合，根据下式更新假设wt：

其 中Φt-1=[ϕ(x1)，ϕ(x2)，…，ϕ(xt-1)]∈Rd×(t-1)，且yt-1=[y1，y2，…，yt-1]∈R1×(t-1)，t=2，3，…，T。

将这种方法称为跟导在线核回归。该方法的精度比在线梯度下降方法更好，但运行时间会更长。每当新的样本xt到来，用近似核得到ϕ(xt)，然后将这一列向量加入到矩阵Φt-1以得到Φt，类似地，将yt加入向量yt-1以得到yt。根据梯度下降公式，每回合都必须计算，所以学习过程中主要的计算代价依赖于假设更新这一步骤。

关于协方差矩阵的计算，有很多种加速的方法。考虑将矩阵Φ近似为一个低秩矩阵，然后再计算其协方差矩阵。如果需要逐行或逐列地得到一个低秩近似，有很多流行的方法可以选择，如CX 分解、CUR 矩阵分解[22]、Nyström 近似等。素描技术也是一个很好的选择，可以应用一些基于随机采样或随机投影的素描技术，但本文选择基于奇异值分解（SVD）的FD 算法来加速大规模协方差矩阵的计算。

2.2 素描在线核回归

根据上述分析，更新假设的关键问题已经转换为更新协方差矩阵的问题，接下来考虑应用FD 算法来加速计算。

通过FD 算法得到Φt的近似，然后计算的协方差矩阵，即为的近似。矩阵Φt∈Rd×t的规模会随回合数增加，即t会线性增加，但是会一直保持d×c的规模，所以的规模也会一直与规模相同。将这个加速版本的算法称为素描在线核回归算法，具体如算法2。

算法2 素描在线核回归算法。

算法可以分成两部分来看。在第一部分，构建了支持集Q。对于每个新样本xt，算法预测其回归值，如果其对应的损失非零，则将它加入支持集。重复这个过程直至支持集的大小达到提前设定的预算值b。支持集Q就这样确定下来，在算法的剩余部分都不会再改变。

在第二部分开始前，根据Qt构建核矩阵。分解，得到核矩阵的奇异向量和奇异值。然后初始化wt，其中αi是第i个支持向量的系数，i∈[b]。这个求解的过程详见文献［8］。

在第二部分，根据每个新样本xt构建ϕ(xt)，则有wTϕ(x)=[α1，α2，…，αB](κ(x，)，κ(x，)，…，κ(x，))T。这个过程和FD 逐行处理的算法过程非常契合。所以根据FD可以得到Φt的近似。预测之后，再根据所有过去t回合的累计损失的平均梯度来更新得wt+1。

为了后续理论分析，除了平方损失具有凸性这一性质，这里还会给出一些损失函数的性质和本文的一些假设。

定义1给定一个线性函数空间F ⊆Rd，∀w、w′∈F，如果一个函数ℓ：F→R 满足不等式

则ℓ 被称为是β-光滑的。

引理1如果一个函数ℓ：F→R 是β-光滑的，∀w、w′∈F，有

假设1 ∀w、|w|≤C，损失函数ℓ 满足‖ℓ′(w)‖≤L。该假设旨在表示出损失函数ℓ 的利普希茨（Lipschitz）常数。

假设2 ∃σ≥0，∀w、w′∈F，则函数ℓ 有下述界

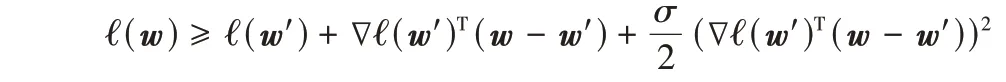
3 理论分析

本章将分析一些本文涉及的理论结果。首先定义T回合的在线学习算法的后悔为：

令ℓ(wTϕ(x)；y)：Rd→R为平方损失函数，可以将SOKR的后悔RS分为四部分来分析：

其中w*为理论上的最优假设（若能提前获知所有样本）；而当应用Nyström 方法做核矩阵近似并进行学习时，wN为理论上的最优假设（若能提前获知所有样本）；在学习的第t回合中，应用在线梯度下降更新得到的假设为wt；而将瞬时损失替换为累计损失再做梯度下降（即F-OKR 的思想）得到的假设为；最后，为SOKR 算法在第t回合的假设，与的区别在于其更新时应用了素描技术。注意到，F-OKR 的后悔为RF=RB+RC+RD。

另外，从T个样本x1，x2，…，xT中导出一个核矩阵K，然后应用Nyström 方法得到其近似。下面给出两个方法的后悔理论。

定理1，t∈[T]表示F-OKR 方法生成的假设序列。假设常数L是所有迭代中梯度的范数界，即利普希茨常数，λ为正则化参数，η为学习率（步长）。令fN(x)=(x)为应用了Nyström 核近似后的最优假设，则F-OKR 有一个后悔上界为：

这个后悔界的结果和NOGD 的后悔很相似，因为这个方法的框架参考了NOGD，但是直觉上来讲，这个方法的后悔界应该比NOGD 的更紧。这个想法将会在后续的实验中验证，具体表现为F-OKR 的回归精度明显好于NOGD。

与F-OKR 不同的是，SOKR 需要考虑素描算法造成的后悔，所以SOKR 的后悔界会更松弛一些。在这一章的最后会对这两种方法的后悔界进行讨论。

与后面的实验结果相对应，SOKR 的回归精度与F-OKR相当，但仍远优于NOGD。

定理2，t∈[T]表示SOKR 生成的假设序列。假设C为任意w∈F 的范数界，即‖w‖≤C，p为空间中任意向量，则SOKR 有一个后悔上界为：

本章剩余部分将会分别讨论后悔RS的各个部分。

3.1 素描算法造成的后悔界

首先需要分析由于应用了素描技术而造成的后悔界，即FD 算法导致的后悔界RA。考虑到平方损失的性质，如果一个损失函数ℓ：F→R 是凸函数，则∀w、w′∈F，有

所以结合ℓ(w)的凸性，有：

其中L是损失函数的利普希茨常数。将和的更新公式代入可得上述最后一个式子。与此同时，已知文献［24］中的引理2 可引用于此。

引理2设是对矩阵Φt应用FD 方法的输出矩阵，则有且

其中：c为素描规模，为矩阵的迹。

将式（1）代入，RA可以重写为：

将的相关项都替换掉，则若可以界定，就能界定RA。

该式由矩阵的谱范数的三角不等式导出，ϕ(x)为空间中任意向量，将其简记为p。

对任意矩阵A，B∈Rn×n，都有tr(mA+nB)=mtr(A) +ntr(B)，所以

由此可以得出：

上式由矩阵谱范数的定义式推得，其中用λm表示矩阵的最大奇异值。

总结这一部分，如果tr(ppT)为一个常数，则这一部分后悔界可得：

3.2 梯度下降法造成的后悔界

这一部分将RB和RC放在一起分析，即。因为RB+RC这部分后悔是一个梯度下降法的变形造成的。

应用梯度下降更新，其中用到的是前t回合在上的累计损失的平均梯度，即。

又因为ℓ 为凸函数，得：

结合式（4）、（5），并在t∈[T]上求和，得：

其中L为利普希茨常数。

这样就得到了梯度下降法造成的后悔，与在线梯度下降的后悔相当。如果选定合适的学习率η，则可以保证该后悔界是亚线性的。

3.3 Nyström近似法造成的后悔界

通过一个固定的支持向量集来得到核矩阵K的近似矩阵，两个方法皆是如此。具体应用的方法为Nyström 近似法，该方法是一个基于列采样技术的高效方法，用于获得矩阵的低秩近似。

在这一部分中，将会分析由核近似造成的后悔界。这一理论结果在文献［20］中的引理1 中已经给出。

引理3定义L(w)为：

令w*为用准确核矩阵K进行学习的最优解，而wN为用近似核矩阵进行学习的最优解，近似核矩阵由Nyström 方法求得，则有：

结合上述引理，则在方法中有：

如文献［8］的引理1 所述，核近似差的谱范数‖K-，其中b为预算值。

3.4 F-OKR的后悔界

3.5 SOKR的后悔界

为了分析SOKR 的后悔，必须要考虑到素描技术造成的后悔，所以需要确认RF加上素描部分的后悔是否还保持亚线性。

如定理2 中所见，将RF和RA两部分后悔合并，当设定，c≪T为任意常数时

4 实验与结果分析

本章将会给出F-OKR 和SOKR 的实验结果，用到的标准数据集在表1 中列出。

表1 选定的数据集信息Tab.1 Information of selected datasets

实验涉及F-OKR、SOKR 和NOGD 算法。实验旨在说明，在不同的数据集上：1）SOKR 相较于NOGD 提高了回归精度；2）FD 算法的引入使得SOKR 的运行时间相对F-OKR 大幅减小，同时精度不受影响。

首先，实现第1 个算法F-OKR：设置径向基函数（Radial Basis Function，RBF）核，应用Nyström 方法近似核矩阵；用平方损失函数，并用过往回合累计损失的平均梯度来更新假设，这个思想与FTL 算法是一致的；然后，应用FD 算法来近似计算梯度时会出现的协方差矩阵，本文主要的算法SOKR，可看作是F-OKR 的加速版本；最后实现NOGD 算法作为对比实验。

现在讨论参数的设置。在前面的章节中，建议设b=，c是一个很小的常数。一开始对所有的数据集设b=30，c=5，这个设定符合理论分析中的假设；然后在保证的同时变动其数值，依次设b=50、70并分别进行实验。对比发现，不同预算值下的实验对于三种算法的回归精度都几乎没有影响，而随着b的增大，核矩阵计算越来越复杂，反而会增加运行时间。最终选定b=30 作为一个最合适的预算值来进行实验，在回归精度和运行时间之间获得平衡。

除此之外，对于不同的数据集选用了不同的γ最优值，其中γ是RBF 的核参数，同时根据分析计算得出了每个数据集的学习率η，详见表2。

表2 核参数γ和步长ηTab.2 Kernel parameterγ and step sizeη

重复每项实验10 次，然后计算平均精度和运行时间，图1 展示了在4 个标准数据集上，SOKR 和F-OKR 两种方法以及NOGD 的平均损失和运行时间。通过实验结果可以看出，两种算法的平均损失都低于NOGD，尤其是SOKR 比F-OKR的性能还要更好一些。精度提高的原因是，该目标函数旨在最小化累计损失，常规方法只考虑当前回合的损失的梯度，而SOKR 和F-OKR 考虑所有过往回合的累计损失的梯度，形式上也更接近于在线学习的目标函数。

注意到SOKR 和F-OKR 的平均损失几乎不依赖于样本的数量，即当样本数量很少时，这两种算法也可以得到一个很好的回归精度，4 个数据集上平均损失减小了64%左右。相反，NOGD 的回归精度随着样本量增加到一个程度才会逐渐收敛，当样本量较少时，SOKR 的运行时间比F-OKR 的还要长。这是因为数据量太少时，素描技术的优势无法展现，反而会复杂化原有的计算过程；而当样本量逐渐增加，素描技术的加速效果才得以展现，如图1（d）所示。故当数据集规模较小时，SOKR 的优势不明显，而在适当的数据集上，SOKR 可将运行时间减少16.7%左右。

图1 三种算法在4个数据集上的实验结果对比Fig.1 Experimental results comparison of three algorithms on 4 datasets

F-OKR 在第t回合时，需要计算Φt-1的协方差矩阵，其中Φt-1∈Rd×(t-1)，矩阵乘法时间复杂度为O(Td2)，所以整个学习过程的时间复杂度为O(T2d2)。当应用了FD 算法时，获得一个近似矩阵的时间复杂度为O(dc2)，计算协方差矩阵的时间复杂度降低为O(cd2)，所以SOKR 的时间复杂度为O(Tcd2)，其中c为一个常数且c

从图1 中还可以看到，在样本数逐渐增加后，F-OKR 和SOKR 算法的运行时间也随之增加。这是因为在更新式中涉及矩阵Φt的计算，该矩阵的规模随着在线学习回合数的增加而增加，在大规模的在线核回归问题中，亟需解决这个问题。这里给出一个优化思路：应用随机素描技术对这一计算步骤进行加速，但需注意到不能应用矩阵低秩近似的相关算法，因为具体问题情境下，要求该步骤计算后所得向量的每一个分量都非零，否则会使得最终更新的假设有较大误差。

图中显示NOGD 的求解速度优于F-OKR 和SOKR，原因可以从算法过程中分析。NOGD 算法在进行假设更新时，应用每回合的瞬时损失的梯度，这意味着NOGD 更新的计算复杂度主要来自两个向量相乘，即(xt)；而 在F-OKR 和SOKR 算法中，每回合根据累计损失的平均梯度进行假设更新，这表示每回合更新的计算复杂度主要源于协方差矩阵的计算，即ΦΦT及，因此运行时间会比NOGD 方法更长。

5 结语

本文提出了一个可以提升在线回归学习精度的算法F-OKR；然后基于素描技术设计了一个算法SOKR，该算法可以将计算复杂度从F-OKR 的O(T2)降低到O(Tcd2)，且理论上证明了两种算法的亚线性后悔界。理论证明及实验验证了该方法是高效的，且可以应用于大规模在线核回归问题中。