基于可靠度的钢桁架拱桥施工期间扣索索力优化研究*

康俊涛，赵子越

武汉理工大学土木工程与建筑学院，湖北 武汉 430070

当前斜拉扣挂法已经大范围应用于钢桁架拱桥的施工中，由于结构材料的随机性，施加的载荷以及行为模型中的错误引起的不确定性是不可避免的，在设计中必须考虑这些以确保结构安全性和可靠性，所以扣索索力优化是典型的需考虑不确定因素的多目标优化问题。国内外学者采用了不同的方法求解斜拉扣挂施工的扣索索力，研究桥型多为钢管混凝土拱桥，且大多数的研究都是基于结构参数完全确定性的假设。朱谊彪等［1］采用二次多项式回归的响应面模型作为代理模型并结合非线性回归的方法求解钢管混凝土拱桥扣索索力。徐岳等［2］提出了一种改进的迭代算法，以达到理想线形为目标确定扣索索力。涂光亚等［3］以一次落架的成拱线形作为目标，结合影响矩阵法求解钢管混凝土拱桥的扣索索力。以上方法均是以单一的线形为目标没有直接兼顾到结构受力方面，同时也没考虑到施工过程中的各种随机性。基于可靠度的优化可以考虑不确定性因素的影响，Jin Cheng 等［4］提出了一种针对基于可靠性的优化问题的混合遗传算法，并应用于一个主跨为500 m的大跨度钢桁架拱桥。Jin Cheng［5］提出了一种基于人工神经网络结合一阶可靠性方法（FORM）来解决逆可靠性问题的方法。

但以上优化方法都是针对单一目标进行优化，若选择多个目标进行优化将会使得结构更加合理。本文提出了一种基于可靠性的多目标优化方法。将可靠度作为优化的约束条件，对结构应力、线形或经济成本进行多目标优化，最终得到最优解集，再结合实际工程情况从中选择一个解，这样在保证结构可靠性同时也起到对结构优化的作用。

1 基于可靠度的多目标优化方法

基于可靠性的优化是可靠度计算与设计优化算法相结合的方法。一般包含两个循环：一个用于优化设计的外循环和一个用于可靠性分析的内循环。在结构可靠度分析模块，本文首先采用拉丁超立方体抽样法抽取样本点，带入有限元计算模型获得目标函数值；采用支持向量回归建立代理模型，之后利用一次二阶矩法分析结构的可靠度指标。优化部分包含两个步骤：拟合目标函数、约束函数及多目标粒子群优化。

1.1 基于支持向量机的可靠度计算方法

常用的计算可靠度的方法有蒙特卡洛法和近似可靠度计算方法，如一次、二次可靠度计算方法。前者需要大量抽样以保证可靠度计算精度，后者需要功能函数的显式表达式。由于蒙特卡洛法用于基于可靠度的优化计算时需大量的抽样严重影响计算效率，本文采用一次可靠度方法计算可靠度。

对于钢桁架拱桥这类较复杂的结构，施工期内力、应力位移等数据的显式函数是很难得到的。蒙特卡洛法则需要大量抽样，利用有限元软件反复计算效率太低，故需要利用合适的代理模型来代替复杂的有限元以提高计算效率。常用的方法如二次响应面法、神经网络、Kriging、支持向量回归等，其各有优劣：二次响应面非线性拟合功能较其他几种方法较差；Kriging 法由于拟合函数无法很好地显示表达不能与一次可靠度方法配合使用；神经网络具有网络拓扑结构设计缺乏有理论依据的严格设计程序、局部收敛和过拟合等缺点，这些缺点容易影响计算结果的精度，造成计算迭代过程的不稳定［6］。支持向量回归基于结构风险最小原则，不受样本数量的限制，具有很出色的小样本学习能力［7-8］，本文选取支持向量回归结合一次可靠度的方法求解可靠度。

由以上的功能函数以及一阶偏导的函数表达式，结合一次可靠度方法即可求得可靠度。

图1 SVM参数寻优流程图Fig.1 SVM parameter optimization flowchart

1.2 基于粒子群算法的多目标搜索算法

多目标粒子群优化算法（MOPSO）相较粒子群优化算法（PSO）算法通过增加外部储备集保存算法迭代过程中出现的非劣解，采取适当的更新策略更新每一次迭代中的pbest（个体引导者）、gbest（全局引导者）和外部储备集来解决多目标问题。为了维护所得非劣解的多样性及保证这些解是沿着Pareto 前端均匀伸展的，采用基于自适应网格法的多目标粒子群算法。

外部储备集即非劣解集的更新主要分为三个步骤：①每次迭代后所得粒子与当前非劣解集中的非劣解按Pareto 占优准则比较，若存在支配解或非劣解则添加至非劣解集中。②每次迭代更新后的非劣解集，若存在受支配解时将其剔除。③若非劣解集中粒子数量超出上限，则利用自适应网格法将拥挤程度高的粒子随机剔除。

在进行种群初始化时，随机生成粒子的位置x和速度v，粒子速度和位置更新模块根据文献［9］的方法进行。

1.3 基于可靠度的多目标优化算法模型

本文建立的基于可靠度的多目标粒子群优化模型为

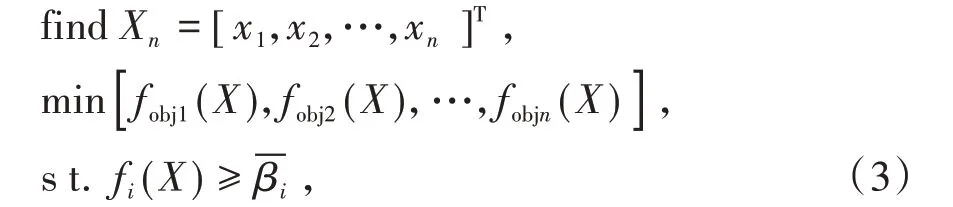
其中Xn=[x1，x2，…，xn]T表示设计变量组成的向量；fobji(X)表示各目标函数（结构的总花费、截面面积、内力应力、位移等）；fi(X)表示约束函数，为结构的某个可靠度指标；-βi表示第i个设计指标要求的可靠度。

该优化过程主要分为两部分：1）可靠度分析流程，包括①利用拉丁超立方抽样法并结合随机变量的特征及概率分布生成随机样本；②利用有限元软件计算各组样本对应的极限状态函数值；③利用样本训练极限状态函数的SVR 代理模型，并测试其精度；④采用一次可靠度方法并结合代理模型求解可靠度指标。2）基于代理模型的多目标粒子群优化，包括：①确定需要优化的设计变量，以及目标函数的指标以及用于约束条件的可靠度指标；②初定设计变量的优化区间，根据实际案例选择优化区间，一般可选择以当前设计方案X0为中心，优化区间为[Xmin，Xmax]；③采用LHS抽样方法，在优化区间抽取设计变量样本点。结合有限元模型，计算每个样本点的优化指标，得到相应的优化指标样本数据；④利用拟合函数拟合设计变量与目标变量的函数关系式；⑤将④中得到的函数关系式作为目标函数并将上述可靠度分析结果作为约束函数，进行多目标粒子群优化求解。具体流程如图2所示。

图2 基于可靠度的多目标优化模型流程图Fig.2 Flowchart of reliability based multi-objective optimization model

2 算例分析

本节利用一个平面简支桁架模型结构作为数值算例，使用前文所述的可靠度分析方法以及多目标优化方法进行优化设计。采用ANSYS 有限元软件中的Beam3 梁单元来建立桁架模型，模型由21 个单元和12 个节点组成，总跨径为6 m；采用圆形截面，截面面积为0.002 m2；在桁架跨中处施加200 kN 集中力；杆件质量密度的设计值为2 500 kg/m3。桁架模型如图3所示。

图3 平面桁架示意图Fig.3 Schematic diagram of plane truss

其中杆件分为3 类即上弦杆、下弦杆和腹杆。选取了6 个随机变量，其中Ai表示第i种杆件的弹性模量；Bi表示第i种杆件的面积。假设上述变量之间均无相关性，其中6 个变量分布情况如表1所示。

表1 随机变量统计特征Table 1 Statistical characteristics of random variables

三类杆件的初始截面面积均为0.002 m2，选取杆件的应力作为可靠度的研究对象，材料的容许应力值取为σ= 160 MPa。

2.1 可靠度分析

同时采用五种方法来求解可靠度：（1）直接蒙特卡洛法，采用拉丁超立方抽样500次带入有限元模型计算得出可靠度（MC）；（2）采用二次响应面为代理模型，并结合FORM 求解可靠度（RSM+FORM）；（3）采用BP 神经网络为代理模型结合FORM 求解可靠度［10-11］（BP+FORM）；（4） 采用SVR 作为代理模型并结合FORM 求解可靠度（SVR+FORM）；（5）采用SVR 作为代理模型并结合蒙特卡洛求解可靠度（SVR+MC）。图4 显示了不同样本下各种方法所得下弦杆的可靠度数值的变化趋势。

图4 五种方法不同样本数量下可靠度计算结果Fig.4 Calculation results of reliability using 5 methods and different quantities of training samples

由图4可看出，直接蒙特卡洛法与二次响应面模型结合FORM的方法计算误差都很大，而其他三种模型在样本数量大于200时效果相差不大，SVR模型在样本数量小于200时波动较小，拟合效果略好于BP 神经网络。而，SVR 结合蒙特卡洛法，与SVR结合FORM 的方法计算结果几乎一致，误差很小，而SVR 结合FORM 的方法的计算效率明显优于蒙特卡洛法。故选择SVR 结合FORM 的方法计算可靠度。

最终计算所得的三类杆件的可靠度分别为1.14、6.535、11.64。分析可知下弦杆失效概率为17.1%，存在较大的安全隐患，有必要对其进行可靠度的优化。

2.2 基于可靠度的优化

在提高可靠度的同时，需要考虑其经济性和跨中的挠度。为了达到上述优化目的，本文对三类杆件的面积进行优化，提高可靠度的同时使得结构总质量以及跨中位移尽量减小，建立多目标优化模型

模型中B1，B2，B3表示三类杆件的截面面积；δ(x)为桁架结构跨中竖向位移；W(x)为结构总体积； min[fbbeta(X)]为优化约束函数，表示三类桁架杆件的应力可靠度的最小值应满足设计要求β0，本文中β0取值为2.5。表2 为算法搜索到的非劣解集合。

表2 非劣解集Table 2 Pareto solutions

由上述结果可看出非劣解集中跨中位移值均在区间［6.582 mm，9.222 mm］，结构总体积在区间［0.065 9 m2，0.090 5 m2］，跨中挠度容许值为l/1500 = 8 cm，故选择第一组解。对优化前后进行对比，结果如表3。

表3 优化前后对比Table 3 Comparison before and after optimization

由表3可知，通过优化后的结果可以看出，下弦杆的可靠度指标由1.143 增加至2.664，最小可靠度为2.664，对应的失效概率为0.1%；同时总体积由0.093 9 m2减小至0.075 7 m2，相对于初始状态减少了约19.4%。跨中位移由于腹杆面积的减小导致略有增大，但也小于l/1500 即8 mm，故优化后结构可靠性大大提升，材料节约19.4%，同时跨中位移也满足要求，优化效果显著。通过算例验证了本文提出的基于可靠度的多目标优化方法的可行性，同时采用SVR代理模型结合FORM计算可靠度提高了计算效率，且计算精度好于二次响应面，略好与BP神经网络。

3 钢桁架拱桥扣索张拉方案优化

3.1 工程概况

某下承式钢桁架拱桥主桥跨径布置为（70 m+240 m+70 m），主桥拱肋由2 片拱肋桁架和8 道横联组成，2 片拱肋桁架横向中心间距38.2 m。每片拱肋桁架由上弦杆、下弦杆和腹杆组成，在拱顶处上、下弦杆竖向中心间距7 m。下弦杆采用抛物线方程，矢高54 m，矢跨比1/4.444，上弦杆采用二次抛物线和圆曲线相结合，见图5。

图5 钢桁架拱桥立面图Fig.5 Elevation drawing of the steel trussed arch bridges

本案例桥梁使用斜拉扣挂法和缆索吊装施工技术，先依次对称吊装拱肋及风撑直至拱肋合龙，再由边跨向中跨对称施工主梁至主梁合龙。施工期间扣索索力承担了大部分拱肋的重量，扣索可以增加施工过程中结构的刚度、减小主结构的内力，施工过程中的标高控制也与索力息息相关。而在施工过程中存在许多不确定性因素，可能会出现扣索失效的情况，所以施工过程扣索的可靠性分析尤为重要。故将三根扣索的初张力作为待优化变量F1，F2，F3。

3.2 扣索可靠度分析

影响施工期扣索索力大小的因素有很多，本文选取钢梁重度γg，钢梁弹性模量Eg，1#、2#、3#扣索的初张拉力F1、F2、F3，以及三根扣索的抗力R1、R2、R3。

在施工进行期间，影响扣索抗力R的影响因子有很多，依据并结合钢桁架拱桥施工方案已基本确定的条件下，考虑影响较大的设计变量，为：扣索材料特性的不确定性、扣索截面几何参数的不定性和计算模式的不确定性，分别用随机变量KM、KA、KP表示。依据文献［12］，考虑KM、KA、KP均服从正态分布，KM的均值和方差为1.14、0.024；KA的均值和方差为1.13、0.14；KP的均值和方差为1、0.10。得到扣索的抗力模型

式中fk为扣索抗拉强度标准值，扣索材料采用抗拉强度为1 860 MPa 的钢绞线。按设计方案三根扣索的规格分别为15φ15.2，18φ15.2，18φ15.2。由此可以确定三根扣索的抗力的统计特征。根据以上分析并结合参考文献［13］的统计结果，上述5种因素的统计特征如表4所示。

表4 随机因素统计特征Table 4 Statistical characteristics of random variables

由图6可知，由于施工顺序的推进，扣索索力呈现一定的变化趋势：1#扣索在安装2#风撑阶段扣索索力达到最大，之后由于2#扣索的张拉导致1#扣索部分松弛；同理2#、3#扣索分别在安装7#拱肋及安装9#拱肋时达到最大，且在扣索索力调整时，索力变化趋势依旧如此。由于三根扣索在扣索索力最大最不利，易达到极限状态，于是将最大索力fi(x)作为目标函数值。

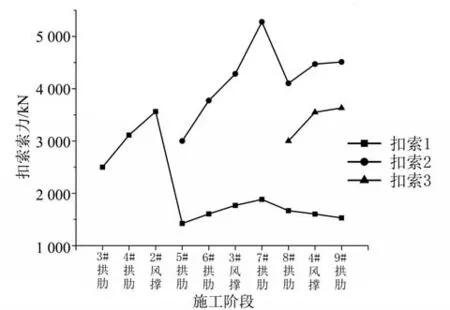
图6 不同施工阶段扣索索力变化趋势Fig.6 The trend of the tension of buckle cable at different construction stages

故极限状态方程为

式中ri(x)为第i根扣索的抗力，fi(x)为第i根扣索施工过程中达到的最大索力。

采用拉丁超立方抽样的方法抽取200 组数据，五个变量取值范围为[μ- 3δ，μ+ 3δ] （μ、δ分别表示随机变量的均值与标准差），并结合有限元分析得出目标值作为样本（其中180 个作为训练样本，20 个作为测试样本）。其中，fi(x)由180 个训练样本结合支持向量回归拟合得到，并与二次响应面的方法和神经网络方法对比。代理模型预测值与抽样点的匹配程度由误差平方和S确定。

初始张拉方案下，1#、2#、3#扣索的初张拉力分别为2 500 kN、3 500 kN、3 000 kN。将SVR和FORM 结合的可靠度计算方法，与SVR 模型和107次蒙特卡洛抽样结合计算所得的可靠度指标对比，结果如表6所示。

由表6可知，两种方法计算可靠度结果误差很小，SVR和FORM结合计算可靠度的方法可以保证计算精度，且计算效率大大提高。目前，针对施工期PC刚构桥的目标可靠度指标，有关规范［14］并没有明确的规定。根据美国AASHTO 规范［15］，施工期结构的可靠度指标为3.5，而对于扣索这类临时结构，可靠度大于2.5 时失效概率就小于0.62%，可以满足施工安全的要求，故取容许可靠度指标为2.5。由以上计算结果可知，1#、2#扣索可靠指标较小，均小于2.5。但，2#扣索失效概率为7%，存在较大安全隐患，应对索力进行优化。

表5 误差平方和计算结果Table 5 Sum of squares of error

表6 扣索可靠度指标计算结果Table 6 Reliability index of the buckle cable

3.3 基于可靠度的扣索索力优化

为保证结构的施工安全和正常使用，需要采取措施控制扣索的失效概率，同时还应兼顾到应力和成桥线形，本文通过调整3根扣索的张拉力对应力及线形两个目标进行优化，同时保证扣索可靠度指标在2.5以上。

其中，应力考虑施工至合龙时结构最大应力，通过有限元分析可知，最大应力出现在拱脚下弦杆处的应力。对于斜拉扣挂施工的拱桥线形优化，可取计入预拱度的拱肋坐标线形为目标安装线形，即以计入预拱度的坐标建立有限元模型，则施工至全桥合龙拆除扣索后，若各关键节点处于设计位置，即认为满足合龙目标线形要求［16］。因此取施工至成桥阶段1～17#吊杆处桥面高程与设计高程的偏差的范数为待优化的目标函数，当位移值为0时，则表示完全满足合龙目标的线形要求。位移值越小表示线形越好，越有利于施工时的位移控制，既保证拱肋变形不至太大，又为以后的线性规划提供充足的可行域。

建立多目标优化模型

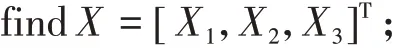
模型中σ(x)为拱脚处的最大应力；h(x)为线形优化目标函数；Δi(x)为施工至成桥阶段第i#吊杆处实际高程；Δi为第i#吊杆设计高程；min[fbbeta(X)]为优化约束函数，表示三根扣索的可靠度的最小值应满足设计要求β0，本文中β0取值为2.5；|X0|为优化初始值。通过多目标粒子群进行优化，表7为算法搜索到的非劣解集。

表7 非劣解集合Table 7 Pareto solutions

由上表可知，非劣解线形目标大多集中在21.3 cm＜h(x)＜26.7 cm，而应力非劣解多集中在135 MPa ＜δ(x) ＜142 MPa。考虑到应力变化较小且富裕度较大，故选择线形优化较为明显的解的第7组解，同时保证一定的应力优化，选择其中一个非劣解，1#、2#、3#扣索初张力分别为2 172 kN、1 542 kN、1 867 kN。在实际施工中，1#、2#、3#扣索张拉值为2 128、1 606、1 930 kN，实际张拉值与优化后张拉理论值误差均不超过5%。优化前后施工至拱合龙肋阶段位移误差的理论计算值以及实测值如图7所示。

由图7可知，优化后的理论线形误差相较于优化前明显降低，且由于2#扣索的索力调整较大，导致8-12#吊点处的线形优化较为明显。同时施工至拱肋阶段时，实测的线形误差与优化后的理论值误差大致吻合。各吊点处实测线形与设计线形最大误差为19 mm，基本满足线形控制的要求。

图7 线形优化前后对比Fig. 7 Comparison of bridge line before and after optimization

从表8可以看出，优化后三根扣索的可靠度均大于2.5，且2#扣索可靠度由1.477 增加至2.616，可靠度最小的1#扣索失效概率为0.41%。优化后的失效概率在1%以内，对于扣索这类临时结构可以满足施工的要求，保证了施工的安全。同时线形累计误差由29.3 cm 降低至21.3 cm，最大拱脚处应力由140.6 MPa 减小至138.7 MPa。通过扣索初张力的优化使得扣索可靠度满足要求，线形也有了明显的优化，同时拱脚最大应力相对于原方案略有减小，并未造成整体结构受力性能的降低。

表8 各项指标优化前后对比Table 8 Comparison of indicators before and after optimization

4 结 论

1）使用支持向量机与一次可靠度计算方法求解可靠度，与蒙特卡洛法相比大大提高了效率，且对于小样本问题其计算精度优于神经网络与一次可靠度结合的方法。

2）将基于可靠度的优化与多目标优化结合起来，可同时优化多个目标函数，并考虑结构中不确定因素的影响，优化得出的不再是唯一解而是非劣解集，可以供决策者根据具体情况选择合适的解，较仅考虑单一目标的优化更加合理。

3）将上述方法应用于某下承式钢桁架拱桥的扣索索力优化，保证扣索可靠度指标均大于2.5的前提下线形累计误差减小约27.3%，同时优化了结构应力。该方法也同样适用于钢桁架拱桥的成桥状态索力的确定。