周期排列抛物形系列沟槽引起的线性水波Bragg共振及共振相位上移*

潘俊杰，刘焕文，李长江

（1.浙江海洋大学 船舶与海运学院，浙江 舟山 316022；2.浙江微昊工程技术有限公司，浙江 舟山 316000）

引 言

Bragg 共振(Bragg resonance)是一类特殊的共振现象，最早由Bragg 父子于1913 年在对X 射线通过晶体引起的反射进行实验时所发现[1].通过理论分析，他们建立了著名的Bragg 共振原理：当晶体间距为X 射线波长一半的整数倍时，X 射线的反射达到最大.这一原理在固体力学甚至整个物理学中得到广泛应用，如光纤光栅传感器和光纤光栅滤波器等，而Bragg 父子也因为此重要发现于1915 年双双获得诺贝尔物理学奖.

Bragg 共振现象后来被发现在其他很多领域同样存在.至于在水波领域的拓广，主要始于Davies[2]的工作.他利用常规摄动分析，导出了水波越过正弦沙纹海底时Bragg 共振的激发条件：正弦沙纹的波长为表面入射波波长的一半.该结果同时得到了实验数据[3-4]的印证.这些早期的开创性工作引发了大量有关正弦沙纹地形激发Bragg 共振反射的后继性研究[5-19].

受正弦沙纹海底激发Bragg 共振形成驻波护岸甚至驻波造陆的启示，Mei 等[20]于1988 年首次提出人工沙坝的概念，建议在近岸波浪破碎带之外修建与岸平行且等间距周期排列的人工沙坝.相比于传统防波堤，系列人工沙坝具有诸多优点：第一，因没于水下，沙坝两侧的水体和鱼类等生物均可以不受阻碍地自由交换，而且堤上容易长出苔藓，可吸引浮游生物的聚集，有利于改善海域环境和保持海洋生态系统.第二，沙坝浸没水下，不会产生视觉冲击，破坏近海景观环境.第三，坝顶可设计成低于平均低潮位，小型船舶航行不受影响.第四，多个小沙坝散布在较宽海床，不会给不够坚硬的海底增加大的承重.最后，科学合理地布置沙坝，使之满足Bragg 共振条件，即沙坝间距约为当地入射波波长一半，则能对入射波产生强反射.

人工沙坝的概念自提出以来，受到了学者们的广泛关注[21-26]，2015 年前的研究进展可参见文献[27].2016 年，Liu 等[28]除了采用物理实验研究半圆形人工沙坝的Bragg 共振，同时针对半圆形的特殊形状运用多极展开和极坐标变换，使得对半圆形沙坝上方的变水深地形不需采用分段常水深的台阶系列去近似逼近，也可以直接进行特征函数展开.2017 年，Zeng 等[29]建立了线性长波越过斜坡上系列矩形沙坝时反射系数的解析解.2020 年，Liu 等[30]构造了线性水波越过梯形人工沙坝时修正缓坡方程的Taylor 级数形式的解析解.他们第一次揭示了当梯形沙坝相对于入射波长的无维化上底宽、下底宽以及无维化水深和浸没深固定时，反射系数是关于沙坝间距相对于表面入射波波长的无量纲变量两倍的周期函数，且周期为1.这说明海底地形波动和表面水波波动的周期性能够通过反射系数的周期性表现出来.他们还发现Bragg 主振的振幅并非总是大于其他所有高阶Bragg 共振的振幅.另外，随着梯形沙坝宽度或高度的增加，Bragg 主振峰和高阶共振峰的相位向低频下移的现象变得越来越明显.

最近, 受抛物形镜面对太阳光线聚焦作用的启发, Zhang 等[31]首次将直线平行的周期波动地形改进设计成V-形弯曲后的周期波动地形, 使之可同时形成水波的Bragg 共振和聚焦双重效应, 为增大波能的提取效率开启了新的思路.Hao 等[32]在此基础上将其拓广设计成抛物形弯曲后的周期波动地形.

海底地形中除了周期排列的正弦沙纹和周期排列的系列人工沙坝可引起水波的Bragg 共振反射以外，互相近似平行且周期排列的沟槽系列同样会引起水波的Bragg 共振反射.最近，有关水波越过周期排列的系列沟槽所导致的Bragg 共振反射已有学者开始进行研究.2018 年，Kar 等[33]采用边界元法数值研究了水波越过海底沟槽的情形.2020 年，Kar 等[34]研究了线性浅水波越过海底斜坡上系列矩形沟槽时的Bragg 共振，结果显示，带有海底斜坡的系列矩形沟槽比不带海底斜坡的系列矩形沟槽导致的Bragg 反射要强.2021 年，Guo等[35]基于Liu 等[36]建立的波浪被单个旋轮线形潜堤和沟槽反射的修正缓坡方程解析解，进一步解析研究了旋轮线形Bragg 潜堤和沟槽对线性波的Bragg 共振反射，第一次发现了当水波越过周期排列的一列沟槽时，Bragg 共振反射的主振相位及高阶共振相位均出现频率上移的现象.这与正弦沙纹地形或周期人工沙坝激发的Bragg 共振所呈现的特点截然不同.在此之前我们熟知的是，当水波越过海底正弦沙纹地形或周期排列的系列沙坝时，Bragg 共振反射的主振及高阶共振的激发频率均小于传统Bragg 原理所预测的频率，称之为频率下移(frequency downshift)或相位下移(phase downshift).频率下移现象引起了众多学者的兴趣和关注，对正弦沙纹地形激发的频率下移现象的研究参见文献[8-9, 11]，对人工沙坝激发的频率下移现象的研究可参见文献[24-25, 28, 30, 37].最近，Liu 等[38]基于Bloch 波的能带理论研究了线性浅水波越过抛物形和半余弦形两类人工沙坝的频率下移，而Liang 等[18]则基于Mathieu 不稳定定理给出了预测主振偏移性质的定量公式.Guo等[35]所发现的与以往完全不同的频率上移现象表明，周期排列的系列沟槽和系列沙坝分别激发表面波产生Bragg 共振反射的激发频率有着本质的不同，值得进一步研究.

由于Guo 等[35]仅仅研究了水波被周期排列的有限个旋轮线形沟槽反射的情形，那么一个自然而然的问题就是，Bragg 共振反射峰值的相位上移现象是否对有限周期排列的任意形状的沟槽而言都是普遍现象呢？换言之，到底是有限周期排列的任意形状沟槽都将引起相位上移现象，还是仅仅只有具旋轮线形状的有限周期系列沟槽才会引起相位上移现象？为了回答此问题，本文中我们基于修正缓坡方程[10]，拟进一步解析研究线性波越过海底周期排列的有限个抛物形沟槽时的Bragg 共振反射.首先，我们将每个抛物形沟槽所在的区间分为两个单调子区间.然后在每个小区间上引入变量替换，使得带隐函数系数的修正缓坡方程转变为系数全部为显函数的等价微分方程，据此构造了等价微分方程的Frobenius 级数解，并确定了级数解的收敛区域.最后，利用质量守恒耦合条件和两个相邻子区间的公共边界的耦合，建立了N个周期排列的抛物形沟槽引起表面波反射的反射系数的解析公式.基于解析公式，讨论了抛物形沟槽的个数、深度和宽度对Bragg 共振反射的影响.

1 抛物形系列沟槽引起线性水波反射的解析解

考虑海底地形为如图1 所示的N个周期排列的全等抛物形沟槽，其水深函数如下：

图1 有限个周期排列的全等抛物形沟槽示意图Fig.1 A schematic diagram for a finite periodic array of identical parabolic trenches

我们研究一列线性水波在N个全等沟槽上的传播.假定抛物形沟槽较浅，底部变化较缓，比如最大斜率不超过1∶1，则根据文献[10]，自由水面位移函数η(x)满足如下修正缓坡方程：

其中

k(x)为波数，由如下隐式的线性波色散关系决定：

其中 ω为角频率，g为重力加速度.

不妨设具有单位振幅的波浪自左向右传播.易知，在所有常水深区域，修正缓坡方程(2)退化为Helmholtz方程，因此相应的自由液面位移函数容易解出为

其中k0为水深h0对应的波数，AR和AT分别为反射和透射系数，所有复常数AR，AT，A(5j)，A(6j)均待定.

接下来致力于求解变水深沟槽区域上的自由液面位移函数.在第j个沟槽的前壁区间Ij,1=[xj,1,xj,2]上，注意水深h(x)为单调函数，所以存在反函数：

运用Liu 和Zhou[39]与Liu 和Xie[40]建立的求解修正缓坡方程的变量替换技术，在修正缓坡方程(2)中引入如下变量替换：

则利用线性波色散关系(6)的等价形式

可将式(8)改写为

注意到水深函数(1)在区间Ij,1上严格单调递减，易证，由方程(9)和(11)定义的变量替换x→K为1-1 映射.显然，该映射将Ij,1映射到区间[K0,K1]=[k0h0,k1h1]，其中k1为水深h1对应的波数.原来的位移函数η(x)在变量替换x→K后变为新变量K的函数，记为ξ(K)，即

将式(8)代入文献[39]中的显式方程(19)，则本文中关于旧变量x的隐式修正缓坡方程(2)被成功转化为如下关于新变量K的显式常微分方程：

其中

式中

方程(13)尽管已经由隐式常微分方程转变为显式常微分方程，但其系数均为变系数，非常冗长复杂，几乎不可能构造其封闭解.我们退而求其次，接下来致力于构造它的级数解.为此需要先寻找级数展开式的展开点，它必须取在方程(13)的正则奇点，而不能取在方程(13)的本性奇点.容易看出K=K1导致S(K)和T(K)表达式中的分母为零，显然为方程(13)的奇点.接下来我们证明K=K1仅为方程(13)的正则奇点而非本性奇点.

由于tanhK在点K=K1处是解析的，可将tanhK在K=K1处进行Taylor 展开，于是有

因此可得

注意到

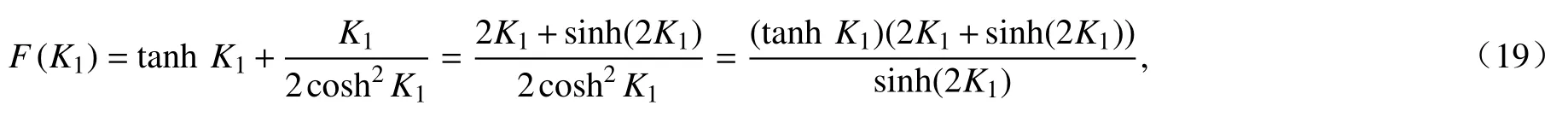
不难证明

这证明了K=K1仅为方程(13)的正则奇点而非本性奇点.于是根据Frobenius 级数理论[41]，方程(13)的通解可以在K=K1展开成如下Frobenius 级数：

其中a0(c)=1，而常数c将由后面出现的指标方程决定.将以上通解代入方程(13)，有

其中(K)=(K-K1)S(K)(K)=(K-K1)2T(K).在方程(23)中令K=K1，并利用式(20)和(21)，得到指标方程c(c-1)+c/2=0，因此解得c1=0和c2=1/2.通过合并式(23)中K-K1的同次幂项，可以递推确定系数am(c)：

其中

由于c1和c2相差一个非整数，所以方程(13)的两个特解可分别表示为如下的Frobenius 级数：

再结合式(12)，区间Ij,1上自由液面位移函数η(x)可表示为以上两个特解的线性组合：

其中A(1j)和A(2j)为待定系数.

接下来考虑第j个沟槽的后壁区间Ij,2=[xj,2,xj,3]，水深函数仍如式(1)所示，但其反函数与前壁区间上的反函数(8)不同，这里变为

同样运用Liu 和Zhou[39]与Liu 和Xie[40]创立的求解修正缓坡方程的变量替换技术，也在修正缓坡方程(2)中引入变量替换(9)，则由线性波的色散关系(10)，式(29)可改写为

注意到水深函数在Ij,2上也严格单调递减，易知由方程(9)和(29)定义的变量替换x→K亦为1-1 映射，它将Ij,2映射到区间[K0,K1].位移函数η(x)在变量替换后变为K的函数，记作ζ(K)，即

将式(29)代入文献[39]中的显式方程(19)，则第j个沟槽后壁区间Ij,2上关于旧变量x的隐式修正缓坡方程(2)被成功转化为区间[K0,K1]上关于新变量K的显式常微分方程：

因为方程(32)与方程(13)在形式上完全一致，故方程(32)的通解也可表为两个特解ξ1(K)和ξ2(K)的线性组合，所以第j个沟槽后壁区域Ij,2上的自由液面位移函数η(x)可表示为

其中A(3j)和A(4j)为待定系数.

为了确定系数AR，AT以及A(Tj)，j=1,2,···,N，t=1,2,3,4，根据文献[42]，自由液面位移函数η(x)需满足如下质量守恒耦合条件：

具体说来，当x=x1,1=0时，条件(34)和(35)变为

其中

当x=xj,1，j=2,3,···,N时，条件(34)和(35)变为

当x=xj,2，j=1,2,3,···,N时，条件(34)和(35)变为

其中

当x=xj,3，j=1,2,3,···,N-1时，条件(34)和(35)变为

其中

当x=xN,3时，条件(34)和(35)变为

最后，结合式(36)、(40)、(41)、(43)、(45)，可得

因此，由N个周期排列的全等抛物形沟槽引起线性水波反射的反射系数的解析解为

当n=1时，式(46)可简化为

其中，W(ξ1,ξ2)=ξ1(K0)ξ2′(K0)-ξ2(K0)ξ1′(K0)，|Π0|为复数 Π0的模，Re(Π0)为复数 Π0的实部.因此有

2 级数解收敛的条件以及判断收敛与否的算例演示

虽然式(28)和(33)给出的是修正缓坡方程的精确解析解，但它们并非封闭解，而只是Frobenius 级数解.实际计算时，对一列具有特定宽度w、水深h0和h1和间距d的抛物形沟槽，外海入射波周期或频率的变化，将引起两个参数K1和K0的变化.而级数(26)和(27)并不是在任何情况下都收敛，它们的收敛是有条件的.本节首先推导出它们收敛的条件，然后通过两个实际算例来具体演示如何判断所构造的Frobenius 级数解是否收敛.

首先考察式(26)和(27)中级数解ξ1(K)和 ξ2(K)的收敛性.注意到方程(13)的所有奇异点如下：

1) sinh(2K)=0的所有复根，即它们全部位于虚轴上，参见图2 中的红色圆点.

2) 2K+sinh(2K)=0的所有复根，参见图2 中的蓝色圆点，其分析可参见文献[39].

3)KtanhK=K1tanhK1的复根，它包含两个实根K=±K1(参见图2 中的两个绿色圆点)以及依赖于水深h1和角频率 ω的一些虚根.因为这些虚根随h1和 ω变化而变化，所以它们在虚轴上的位置并不固定，因此在图2中并未标出，但我们只需记住它们在虚轴上就可以了.

图2 方程(13)除K tanh K=K1 tanh K1的虚根外的所有奇异点Fig.2 Singularities of eq.(13) except for the imaginary roots ofK tanh K=K1 tanh K1

根据Frobenius 级数理论，两个级数ξ1(K)和 ξ2(K)在整个区间[K0,K1]上收敛的充要条件是，以级数展开点K1为圆心，且以K1-K0为半径的复圆盘|K-K1|≤K1-K0不能包含方程(13)的除K1外的任何奇异点.注意到K0＞0，位于虚轴上的所有奇异点不可能在复圆盘之内.而其他不在虚轴上除K1外的所有奇异点中，距离K1最近的奇异点为关于x轴对称的两个奇异点K=1.125 36±2.106 20i.只要这两个奇异点不落入复圆盘之内，则所有奇异点都不会落入该复圆盘内.因此式(26)和(27)中级数解ξ1(K)和 ξ2(K)收敛的充要条件是如下不等式成立：

上述不等式在几何上为一个以三条曲线K0=K1-(K1-1.125 36)2+4.436 078 44，K0=K1和K0=0为边界围成的右边没有边界的开放区域，如图3 所示阴影部分，它即为级数解ξ1(K)和 ξ2(K)的收敛区域.当且仅当点(K1,K0)落在该阴影区域内，ξ1(K)和 ξ2(K)收敛.由图3 可以看出，当K1＜2.6，即沟槽不太深时，对任何K0＜K1，两个级数解(26)和(27)都无条件收敛.而当2.6 ＜K1＜10，即沟槽适当深时，只要K0＞1.009，即海床的整体水深h0不是太浅，则两个级数解(26)和(27)也都收敛.

图3 级数ξ1(K)和 ξ2(K)的收敛区域(即阴影区域)以及两个例子的收敛性分析Fig.3 Convergent regions of ξ1(K) and ξ2(K) and the convergence analysis in 2 examples

接下来，我们将通过两个实际的算例来演示如何判断两个级数解(26)和(27)的收敛性.

正如前面所指出的，当且仅当(K1,K0)落在如图3 所示的阴影区域内，式(26)和(27)中的级数解ξ1(K)和ξ2(K)才是收敛的.

进一步地，为了演示如何准确判断ξ1(K)和 ξ2(K)收敛，第一个例子我们考虑一组抛物形沟槽，其整体水深h0=0.7m，沟槽最深处水深h1=1.2 m.因为级数解的收敛性条件(50)与沟槽个数N、沟槽宽度w和沟槽间距d无关，因此不用设定N，w和d的具体数据.考虑所有满足条件0.03≤K0≤5.0的入射波，此时入射波周期T的变化范围为0.75 s≤T≤55.96 s.由线性波色散关系(10)有

当K0由0.03 变化到5.0 时，通过对以上方程数值求解K1，便可以得出(K1,K0)的移动轨迹如下：

上述(K1,K0)的移动轨迹体现在几何上为一条曲线线段，在图3 中以红色线段标注.因为整条线段全部落在阴影区域中，据此可以断定式(26)和(27)中的Frobenius 级数ξ1(K)和 ξ2(K)均收敛.

第二个例子我们考虑一组抛物形沟槽，整体水深h0=0.2 m，沟槽最深处水深为h1=4.0 m.考虑所有满足条件0.10≤K0≤0.75的入射波，此时入射波周期T的变化范围为1.3 s≤T≤8.99 s.类似于第一个算例，可得到K1随K0变化而变化的如下关系式：

当K0由0.10 变化到0.75 时，对以上方程数值求解K1，亦可得出(K1,K0)的移动轨迹如下：

上述(K1,K0)的移动轨迹为图3 中的绿色线段.因该线段没有完全落在阴影区域，故ξ1(K)和 ξ2(K)对周期T在1.3 s≤T≤8.99 s中的所有入射波并不能都保证其收敛性.若将K0限制在0.1≤K0≤0.45，也即将周期T限制在2.06 s≤T≤8.99 s，则ξ1(K)和 ξ2(K)都将收敛.

3 模型验证：与边界元数值解的比较

考虑等距排列的抛物形沟槽，其参数为N=4，h0=1.0 m，w=4 m，d=7 m，然后让h1变化，分别考虑h1为1 .1 m，1.2m，1.3 m 和 1.4 m 的4 种工况，此时沟槽的无量纲深度H=b/h0分别为0.1，0.2，0.3和 0.4.首先，针对0.002 24≤K0≤2.244，也即0.005 ＜2d/L≤5.0，先采用本文解析模型对这4 种工况进行计算.接下来，为了检验本文解析解的正确性，我们采用边界元数值模型对0.005≤K0≤2.244，即0.011 14 ＜2d/L≤5.0，也进行了计算，其边界元模型由滕斌和侯志莹[43]建立，他们将流域分割为距离沟槽阵列较远的上游流域、下游流域和沟槽所在的中间流域，在上、下游流域对速度势做特征展开，中间流域则采用边界元方法离散求解Laplace 方程，最后将三个区域解联立求解.不过，文献[43]中仅仅计算了地形相对简单的单个对称和非对称二维沙坝和沟槽对波浪的反射，结果表明在缓坡条件下，边界元数值解与修正缓坡方程的解析解[44]吻合得很好.其实，该边界元模型也可用于计算周期排列的有限系列抛物形沟槽引起的水波Bragg 共振反射，不过地形更复杂，因而使得处理起来也更复杂.为了继续验证本文的解析解，我们这里也借用该模型同时计算本节考虑的4 种工况.

在采用边界元模型计算时，计算区域取为[-4(d-w)，Nd+w+4(d-w)]× [-h(x)，0]，在计算区域的边界上总共用到1 600 个二次元单元，其中左右边界均用到50 个二次元单元，而自由面边界和海底地形边界均用到750 个二次元单元，其中每个沟槽上50 个单元，两个相邻间的沟槽之间50 个单元，沟槽区域的前后各用到200 个单元.而采用本文解析模型计算时，依据本文前述级数解收敛的判断方法可以很容易判断出，本文解析模型的级数解ξ1(K)和 ξ2(K)对于上述4 种工况在整个区间0.005≤2d/L≤5.0中均收敛.两种不同模型计算得到的结果参见图4.容易看出，对4 组不同深度的沟槽，采用两种不同模型计算得到的结果几乎完全一致，因为4 种情形下最大的海底地形斜率分别为0.1，0.2，0.3 和0.4，都在修正缓坡方程的适用范围内(即海底地形最大斜率不超过1∶1).两个解相互之间很高的吻合程度佐证了本文解析模型的正确性.

图4 采用本文解析模型和基于Laplace 方程的边界元模型[43]分别计算得到的两个解的比较Fig.4 Comparison between the present solution and the BEM solution[43] to Laplace’s equation

需要指出的是，当2d/L很小时，图4(a)、(b)中边界元解可见翘尾现象，即当2d/L→0时反射系数并不为0，原因是此时相应的入射波波长很长，比如2d/L=0.011 14对应的入射波长为L≈1 256.73 m，因此在数值计算中，若想完整地抓住入射波信息，理论上要求计算区域在沟槽阵列的前后至少应留有一个波长的长度.但是，对于上面考虑的海底系列沟槽的4 个工况，假若沟槽阵列前后真留一个波长的长度，则计算区域应取为[-1 269.23，1 269.23]，而沟槽阵列所在的区域仅为[-12.5，12.5]，导致沟槽阵列在整个计算区域中的相对分辨率不够.因此当2d/L很小时，实际计算区域在沟槽阵列的前后其实又做不到真的留一个波长的长度.图4(a)～(d)中目前呈现的4 个边界元解是在沟槽阵列前后各留有4(d-w)=12 m 进行计算的结果.可见当2d/L很小时，边界元方法中的翘尾现象无法彻底消除.这可能也是很多数值模型都将计算区域的左端点取得离0 有一定距离的原因，例如文献[15]中的图5、6，文献[21]中的图3～7，文献[45]中的图2，文献[46]中的图1～9.但本文为了边界元结果的全域呈现和真实呈现，在采用文献[43]的边界元模型计算时仍令2d/L的最小取值为0.011 14，即K0=0.005.

另一方面，本文解析解并不存在任何翘尾的问题.事实上，当2d/L=0.005时，本文解析解计算出4 个工况下的反射系数值分别为0.001 11，0.002 07，0.002 90 和0.003 64.此时入射波波长为2 800 m，4 个宽度仅为4 m，高分别为0.1 m，0.2 m，0.3 m 和0.4 m 的沟槽对于波长如此长的入射波而言，其影响几乎可以忽略不计，因此从物理上推断，其反射系数显然应接近于0，这个推断与本文解析解计算的结果完全符合.解析解与边界元解在这一点上的差异也反映出寻找解析解的重要性，除了计算机位数引起的舍入误差(也即机器误差)外，解析解不存在任何截断误差.因此解析解和实验解都被作为检验和验证数值解的标准，但解析解的获取成本却远远低于实验解的获取成本.

4 本文解析解与线性摄动解析解的比较

基于经典的一阶摄动法，Miles[47]建立了连续微幅波动海底地形或障碍物引起表面波反射的反射系数的通用解析公式如下：

其中δ(x)为海底地形或障碍物的形函数，其高度从海底的平均深度h0算起.将该通用解析公式具体应用于本文的抛物形系列沟槽，注意到相应的形函数为

可得反射系数的经典摄动解析解如下：

值得指出的是，Miles 的通用公式(55)是基于经典的一阶摄动法导出的，其适用条件仅限于摄动法的小参数假设，即沟槽的无量纲深度H必须很小.另外，从式(57)的第二式可知，当沙坝间距d为入射波半波长L/2的整数倍时，若N足够大，则反射系数RMiles有可能无界，说明Miles 的通用公式(55)在N很大时将会崩溃失效.这与Mei[5]指出当沙纹个数足够大时，Davies[2]关于正弦沙纹地形Bragg 共振反射的摄动解析解将崩溃失效是完全一致的.

考虑一列共8 个抛物形沟槽，先固定如下参数：h0=1 m，w=4 m，d=7 m，然后让h1变化，分别取h1为1.05 m，1.15m，1.25 m 和1.35 m，此时沟槽的无量纲深度H分别为0.05，0.15，0.25和0.35.分别采用本文基于修正缓坡方程的级数形式解析解模型和Miles 基于经典一阶摄动法的封闭形式解析解模型对此进行计算，计算结果参见图5.如图5(a)所示，当H=0.05时，采用两种方法计算得到的结果几乎完全一致，这就互相印证了两个结果的正确.但随着H的值逐步增大，即当H=0.15和0.25 时，两个解的差别也随之逐步显现，参见图5(b)、(c)，原因在于Miles 基于经典一阶摄动法的通用公式(55)已经不再适用，因而产生了较大误差.最后，当H=0.35时，基于一阶摄动法的解析解模型完全崩溃，因为采用它所计算出来的反射系数竟然超过了1，达到了1.115 3，这显然是错误和荒谬的.

图5 本文解析解与应用Miles 的通用公式(55)的比较Fig.5 Comparison between the present solution and the solution based on Miles’ formula (55)

作为对比，本文基于修正缓坡方程建立的解析模型并不受小参数的限制，唯一要求的是海底地形变化相对较缓.正如文献[44]所显示的，在计算单个梯形沙坝或沟槽引起的波浪反射时，只要海底地形斜率不超过1∶1，则基于修正缓坡方程的解析模型与文献[48]的基于Laplace 方程的特征函数展开模型(EFEM)的解吻合得很好，参见文献[44]中的图3(b)、5(b)和6(b).因此本文建立的基于修正缓坡方程的解析解与Miles 的摄动解析解相比，其适用范围大，既不受沟槽个数的限制，也适用斜率不超过1∶1 的沟槽.

5 沟槽个数对Bragg 共振反射峰值、带宽和相位的影响

为研究沟槽个数对反射系数特别是共振反射系数的影响，考察具如下参数的系列沟槽：h0=0.7 m，h1=1.2 m，w=2.0m，d=3.0 m，并令沟槽个数N从1 增加到20，计算范围为0.05≤2d/L≤3.0，等价于2 m ≤L≤ 120 m.由第2 节讨论知，本文解析模型中的级数解ξ1(K)和 ξ2(K)对所有20 种情形在整个范围0.05≤2d/L≤3.0中均收敛.相应计算结果参见图6.

可以看出，当沟槽个数N增加时，Bragg 共振反射的所有主振峰值(图6 中以圆点表示)均相应地逐步增加，很快就达到了1.而相应共振带的带宽则随沟槽个数增加而逐步变窄，依据文献[13, 49]，Bragg 共振反射的共振带以无限周期列抛物形沟槽相应的Bloch 波带隙(band gap)为极限，这与有限周期排列人工沙坝导致的现象一致，参见文献[38]的图3 和图11.

图6 抛物形沟槽个数对Bragg 共振反射及共振带宽的影响Fig.6 Influences of the number of trenches on the Bragg resonance and the resonance bandwidth

现在来看Bragg 共振主振发生的相位，它们均向右发生了偏移，即发生在2d/L＞1的位置.在此之前，不少的计算结果，包括数值解[28,49]、实验解[28]和解析解[11,24-26]均表明，由海底周期排列的正弦沙纹地形或人工沙坝导致的海洋表面波的Bragg 共振反射[13]，并不遵循传统的Bragg 原理，精确地出现在2d/L=1，而是出现在2d/L＜1的位置，简称相位下移(phase downshift)，参见文献[8-9, 11].最近，Liu 等[14]建立的基于修正缓坡方程的解析模拟表明，由正弦沙纹地形引起的Bragg 共振，若沙纹个数固定，令沙纹高度增加时，相位下移现象会变得更加明显，参见文献[14]中的图11(c)～(k).Liu 等针对三种特定沙纹地形给出的135 个工况的计算结果进一步揭示出，当正弦沙纹个数大于8 时，Bragg 主振峰的相位将不再随沙纹个数的改变而改变，而是固定不动，参见文献[14]中的表2.当正弦沙纹个数大于12 时，Bragg 高阶共振峰的相位也不再随沙纹个数的改变而改变，也是固定不动，参见文献[14]中的表3.关于人工沙坝系列引起的Bragg 共振相位下移的研究参见文献[24-26].类似地，几乎所有这些早期研究的零星算例(数值的或实验的)都表明，当人工沙坝个数改变时，相位下移的程度也随之改变.而Liu 等[30]针对一类特定梯形沙坝的30 个工况的计算结果则进一步揭示出，前述结论仅对沙坝个数很少的情形成立，一旦沙坝个数相对比较大时，共振峰值的相位下移将不再随沙坝个数的改变而改变，而是固定不动，参见文献[30]中的表1.

回到上面所说的Bragg 共振相位向右边高频方向移动的现象.该现象最近才刚刚由Guo 等[35]第一次观测到.他们研究的是周期排列的旋轮线形系列沟槽所激发的水波Bragg 共振反射，与以前发现的相位下移现象相对照，此现象被Guo 等[35]命名为“相位上移”(phase upshift).本文中，相位上移现象再次在周期排列的抛物形系列沟槽上得到确认，说明了针对周期排列的沟槽地形，它极可能是一个普遍现象.换言之，只要是周期排列的系列沟槽，无论沟槽形状如何(如常见的矩形、梯形、三角形、半余弦、半圆形等)，相应的共振相位就会上移.我们预测，这个最近才刚刚发现的新现象后续有望吸引学者们开展进一步的深入研究.

对于由正弦沙纹和人工沙坝引起的Bragg 共振反射出现的相位下移现象，虽然背后隐藏的定量化数学机理尚不清楚，但关于其定性化的物理机制的解释已经不少.Guazzelli 等[9]将此现象的发生归于瞬逝波模态.Liu 和Yue[11]将此现象的发生归于表面波的非线性性(波陡)，海底地形变化涉及的非线性效应(坡陡)，以及水深条件等因素不能严格满足线性理论的假设.Chang 和Liou[24]将此现象的发生归于沙坝对反射波相速度的减缓.最近，Liang 等[18]基于Mathieu 不稳定理论给出了波浪在正弦沙纹地形上传播时Bragg 共振相位的理论预测公式.

本文研究的是线性波在系列沟槽上的传播，并非系列沙坝上的传播，且没有考虑瞬逝波模态，因此Bragg共振相位上移现象可解释为周期排列沟槽的存在使得水波传播速度加快，因为波浪传播相速度近似与水深的平方根成正比.事实上，对近岸浅水波，相速度可近似简化为可见水越深水波传播速度越快.下面以两个沟槽为例来解释它们所激发的Bragg 共振反射相位上移现象.

首先，假定沟槽非常浅非常浅，根据传统Bragg 原理，Bragg 共振反射发生的条件为：2d=nL，其中n为正整数.其物理解释为，入射波沿x轴正向传播遇到第1 个沟槽时，将产生沿x轴负向传播的反射波和继续正向传播的透射波，为叙述方便，分别称它们为第1 反射波和第1 透射波.第1 透射波继续正向传播距离d后，在遇到第2 个沟槽时又将再次产生负向传播的反射波和继续正向传播的透射波，分别称它们为第2 反射波和第2 透射波.而第2 反射波负向回传距离d后，再经过第一沟槽时又将产生负向传播的透射波和正向传播的反射波，为描述的统一起见，称其中负向传播的透射波为第3 反射波，而正向传播的反射波为第3 透射波.所谓Bragg 共振反射，指的是第1 反射波与第3 反射波正好同相位叠加.由于此时假定两个沟槽都非常浅，因此无论是入射波、反射波，还是透射波，其传播的相速度都可以看做近似相同，记作C.因此，要第1 反射波与第3 反射波同相位叠加产生Bragg 共振反射，则第3 反射波自离开第一沟槽到再次回到第一沟槽期间走过距离 2d所用的时间，必须恰好等于第1 反射波走过其波长L的整数倍n所花的时间，即2d/C=nL/C，也即2d/L=n.

现在假定考虑的两个抛物形沟槽具有一定深度，虽然第3 反射波自离开第一沟槽继续正向传播到被第二沟槽反射后再次回传并穿过第一沟槽所走过的距离仍然为 2d，但是由于沟槽具有一定深度，第3 反射波在通过这个距离 2d时的相速度比原来的要快，假定其平均相速度为C′，则C′＞C.因此，要第1 反射波与第3 反射波同相位叠加产生Bragg 共振反射，则第3 反射波自离开第一沟槽到再次回传后穿过第一沟槽所走过距离 2d所用的时间，必须恰好等于第1 反射波走过其波长L的整数倍n所 花的时间，即2d/C′=nL/C，也即2d/L=C′n/C＞n.显然，此时Bragg 共振反射出现了相位上移现象.

6 沟槽深度对Bragg 共振反射峰值、带宽和相位的影响

为讨论抛物形沟槽深度b对Bragg 共振反射的影响，对如下固定的沟槽参数h0=0.5 m，w=2.0 m，d=3.0 m，N= 4，6，8，10，令沟槽的无量纲深度H取如下5 个值：0.2，0.3，0.4，0.5，0.6，也即b= 0.10 m，0.15 m，0.20 m，0.25 m，0.30 m，然后采用本文建立的基于修正缓坡方程的解析模型计算了当0.05≤2d/L≤3.0，亦即2 m≤L≤120 m 时的反射系数，其结果参见图7.

从图7 可以看出，当沟槽个数N、宽度w及相邻沟槽的间距d都固定的情况下，Bragg 主振峰值随沟槽深度的增加而增加.其次，当沟槽深度增加时，共振带宽也随之增加但增加的幅度不大.最后还可看出，在沟槽个数N、宽度w以及间距d固定的情况下，共振相位随沟槽深度的增加向高频移动的幅度也增加，其原因与前面解释的一致，即沟槽越深，第3 反射波自离开第一沟槽继续正向传播到被第二沟槽反射后再次回传并穿过第一沟槽的平均相速度更快，从而导致共振相位的上移幅度更大.

7 沟槽宽度对Bragg 共振反射峰值、带宽和相位的影响

最后，我们讨论沟槽宽度对Bragg 共振反射峰值、带宽和相位的影响.对如下固定的沟槽参数：h0=0.7 m，b=0.5m (即h1=1.2 m)，d=12 m，N= 4，然后令宽度w分别取1 m，2 m，···，12 m.采用本文建立的基于修正缓坡方程的解析模型对0.05≤2d/L≤3.0，亦即8 m≤L≤ 480 m 时的反射系数进行计算，其结果参见图8(a)～(c).

图8 沟槽宽度对Bragg 共振的影响Fig.8 Influences of the trench width on the Bragg resonance

先看沟槽宽度对Bragg 共振反射峰值的影响.将图8(a)～(c)中标记出的主振反射峰值以及相对应的相位整合至图8(d)中，可以清晰地看出当抛物线形沟槽的宽度w由1 m 增加到8 m 时，Bragg 共振反射的峰值由0.159 18单调增加至0.729 48，但当沟槽宽度w由8 m 继续增加时，Bragg 共振反射的峰值则反而开始逐步降低，一直到w=12 m 时，Bragg 共振反射的峰值降为0.594 97.这就意味着在这个特殊的工况下，Bragg 共振反射的峰值在w=8m 的附近达到最大值.其次还可以看出，抛物线形沟槽的宽度w变化时，Bragg 共振带宽几乎不受影响.最后，在抛物线形沟槽个数N、沟槽深度b以及相邻沟槽之间间距d固定的情况下，Bragg 共振反射的主振相位随沟槽宽度的增加向高频移动的幅度也增加，其原因也与前面解释的一致，即沟槽越宽，水变深的范围更大，第3 反射波自离开第一沟槽继续正向传播到被第二沟槽反射后再次回传并穿过第一沟槽的平均相速度更快，从而也导致共振相位的上移幅度更大.

8 结 论

针对周期排列的抛物线形有限系列沟槽对线性表面波的反射问题，本文构造了修正缓坡方程的Frobenius 级数解.在此基础上，结合矩阵乘法，给出了反射系数的解析公式.为了检验解析解的正确性，我们将其与边界元解进行了对比，发现二者吻合很好，但边界元解对波长非常长的入射波有翘尾现象，意味着一定误差的存在，而本文解析解没有翘尾现象.与Miles 的一阶摄动解的比较反映了本文解析解适用性范围更广，可以适用于深度较大的抛物沟槽(只要沟槽最大斜率不超过1∶1)，而摄动解在沟槽地形斜率很大时可能崩溃失效.

基于本文建立的反射系数的解析公式，我们分别讨论了抛物形沟槽个数、深度和宽度对Bragg 共振反射峰值、带宽和相位的影响.结果表明，当固定沟槽宽度与深度而令沟槽个数增加时，Bragg 共振峰值将随之相应地增大，直到最终达到1，即全反射，而Bragg 共振带宽则逐步变窄，终止于一个固定的宽度而不再进一步变窄.当固定沟槽个数和沟槽宽度，而令沟槽深度增加时，Bragg 共振峰值将随之相应地逐步增大，共振带宽也随之稍微增加但增加的幅度不大.当固定沟槽个数和沟槽深度，而令沟槽宽度增加时，Bragg 共振峰值则先增后减，说明存在一个特别的沟槽宽度，使得Bragg 共振反射峰值达到最大.当固定沟槽个数和沟槽深度，而令沟槽宽度增加时，Bragg 共振带宽基本不变.最重要的是，本文确认了周期排列的有限个抛物形沟槽也将导致Bragg 共振的相位上移.该现象的再次确认说明了，相位上移对于有限个周期排列的任意形状的沟槽地形极大可能是一个普遍现象，原因在于任意形状沟槽的存在都使得水深变深了.另外，计算结果显示，当增加沟槽深度或宽度时，相位上移的幅度也随之增大，因为水深变深的程度随之增大.

致谢本文作者衷心感谢浙江海洋大学科研启动基金(Q1607)对本文的资助和大连理工大学滕斌教授提供的有关图4 中边界元数值结果的计算程序.