基于谱风险度量的SVM求解算法与实证分析

李瑞祺， 韩有攀

（西安工程大学理学院，西安 710048）

支持向量机是机器学习中最成功的分类算法之一. 支持向量机是寻找一个超平面，使该超平面以最大限度地分离不同类别中的训练样本. 目前最具代表性的SVM模型有：C-SVM、V-SVM、EV-SVM. C-SVM的分类权重是由参数C控制的，但由于在实际应用中，该分类器参数C是未知的，需要被提前设定，并且该分类器参数的可解释性也不强，这在应用中会带来不小的麻烦. 为了有效地解决该问题，Schölkopf 等［1］提出了V-SVM模型，该模型的参数无须提前设定，它是通过机器自行学习获得的数值，并且该分类器的参数比原始的C-SVM 的参数有着更好的解释性. 后来Chang 和Lin［2］发现V-SVM 的参数并不能取遍［0，1］之间的数.为了解决这个问题，Perez-Cruz等［3］提出了EV-SVM，该模型通过改变V-SVM模型中的限制条件使得参数V可以取遍［0，1］之间的数. 他们还通过实验证明了EV-SVM的泛化性能优于原始V-SVM模型，该模型不仅有助于阐明V-SVM的理论性质，而且有助于提高其泛化性能.

SVM模型与金融风险度量之间有着紧密的联系. Gotoh等［4］基于金融风险与机器学习之间的关系，提出了金融风险度量与SVM 模型之间的异同点，并使用SVM 模型对金融债券评级进行了数值实验. Takeda 和Sugiyama［5］在V-SVM 的研究基础上提出了EV-SVM 的优化算法. 同时发现了V-SVM模型与金融风险度量中的CVaR之间存在联系，并证实了V-SVM模型可以当作计算CVaR最小值时使用. Gotoh和Takeda［6］通过研究SVM模型与CVaR模型之间的特殊关系，提出了一种获得全局或局部最优解的求解方法，并通过数值实验证实了该求解模型在分类效果预测上有更精确的预测精度. 后来Wang［7］提出了一种基于最坏情况下CVaR最小值的鲁棒SVM模型，该模型可以用来计算最坏情况下的CVaR最小值，实验证明该模型的计算结果要比传统的V-SVM模型精确. 由于谱风险度量不仅有CVaR的优点，还充分考虑了投资者对风险态度偏好的问题，Wang等［8］提出了一种基于谱风险度量最小值的支持向量机模型，并通过数值实验证实了该模型的计算精度比传统的V-SVM 模型精确，该模型在单一权重加和的CVaR 基础上，通过采取不同的权重比例构造了一个多权重加和的风险度量模型. 随后，不断有新的SVM 模型出现，例如：Takeda 等［9］提出了一种基于金融风险最小值的SVM 模型——ER-SVM（Extended Robust Support Vector Machine），实验证实了该分类模型相比于之前的分类模型，有着更精确的分类精度. Takeda和Kanamori［10］提出了一个统一的机器学习模型（Unified Machine Learning Model，UMLM），该模型不仅适用于二分类模型，还适用于回归、异常值检测等模型. 除此之外，还有许多学者研究了支持向量机的理论［11-15］.

此外，我国许多研究学者将支持向量机模型应用到银行信用风险评级研究中去. 余晨曦［16］采用支持向量机模型来研究我国商业银行信用风险识别模型，并与传统的多元判别分析方法进行对比. 通过实验结果的对比容易发现，支持向量机模型判别的误判率明显低于多元线性判别模型的误判率. 葛青青［17］，朱琳［18］同样使用SVM模型来研究金融行业信用风险评级模型，实验证明使用支持向量机模型可以提高分类精度，在金融信用评级预测方面较为精准和有效.

本文根据一致风险度量表示定理，通过求解出谱风险度量的不确定集合表示形式，构造出基于谱风险度量的支持向量机模型，并通过求解该不确定型集合，找到该模型的最优解. 在实证分析方面，与传统的基于CVaR 的支持向量机进行对比. 数据结果表明，基于谱风险度量的SVM 模型比传统的基于CVaR 的SVM 模型计算精度高，误差小.

1 预备知识

定义1.1（谱风险度量） 若φ∈L1(Ω,ℱ,P)，即φ属于L1范数空间，并且满足：①φ≥0；②φ是递减的；③‖φ‖ =1. 则

并指出存在如下等式关系：

其中Xi:N为顺序统计量.

定义1.2（一致风险度量） 设V⊂L1(Ω,ℱ,P)是一实值随机变量集合，函数ρ:V→ℝ 若满足下列条件，则称为一致风险度量：

（i）单调性：任意X、Y∈V，若Y≥X，则ρ(Y)≤ρ(X)；

（ii）次可加性：任意X、Y，若X+Y∈V，则ρ(X+Y)≤ρ(X)+ρ(Y)；

（iii）正齐次性：任意X∈V，h＞0，若hX∈V，则ρ(hX)=hρ(X)；

（iv）平移不变性：任意X∈V，a∈ℝ，有ρ(X+a)=ρ(X)-a.

定义1.3（分布不变性） 设V是实值随机变量集合∀X、Y∈V，若F(X≤c)=F(Y≤c)，满足ρ(X)=ρ(Y)，则称两个随机变量满足分布不变性.

定义1.4（共调性） 若两个随机变量Y1,Y2在L1空间中，若对于所有的ω、ω′∈Ω 有：

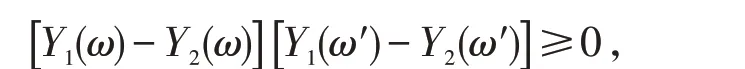
则称两个随机变量Y1、Y2具有共调性.

关于共调性，文献［20］有如下结论：若存在Y1=f(U);Y2=g(U)，f、g是单调递增的函数，U为一个随机变量，且U∈[0,1]，则可以说明两个随机变量Y1、Y2具有共调性.

定义1.5（二阶随机占优） 任意X、Y∈V，若存在一个凸的、单调函数ψ，满足：

则称随机变量Y二阶随机占优于随机变量X，即X≺SD(2)Y.

2 谱风险度量的性质

命题2.1（谱风险度量满足一致性） 设V是一实值随机变量集合，谱风险度量是一致风险度量.

即Mφ(X)≥Mφ(Y)，证明完毕.

（ii）次可加性. 根据定义1.1有：

证明完毕.

证明完毕.

由命题2.1知，谱风险度量是一致风险度量. 除此之外，它还具有如下的性质.

命题2.2（谱风险度量满足分布不变性） 设V是一实值随机变量集合，∀X、Y∈V，若F(X≤c)=F(Y≤c)，则Mφ(X)=Mφ(Y) .

所以，Mφ(X)=Mφ(Y). 证明完毕.

命题2.3（谱风险度量满足共调可加性） 若Y1和Y2都满足共调性，则有：Mφ(Y1+Y2)=Mφ(Y1)+Mφ(Y2).

证明 具体证明过程见参考文献［21］.

命题2.4（谱风险度量满足二阶随机占优） 设V是一实值随机变量集合，任意X、Y∈V，存在一个凸的、单调的函数，满足：

证明 根据定义1.1谱风险度量辅助函数定义

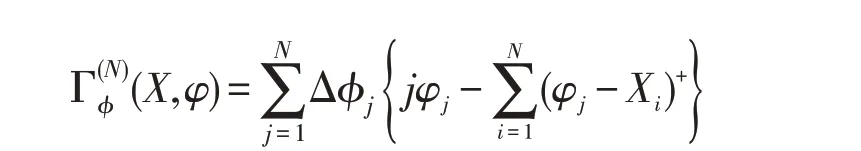
3 基于谱风险度量的SVM模型

本部分将给出基于谱风险度量的SVM形式，为此先介绍一致风险度量的表示定理.

命题3.1［4］（一致风险度量表示定理） 若ρ是一致风险度量，则ρ可有下面表示：

3.1 基于一致风险度量的SVM模型

首先给出最基本的SVM模型［4］：

把损失函数作为随机变量，考虑损失函数在一致风险度量下的SVM模型. 由命题3.1得：

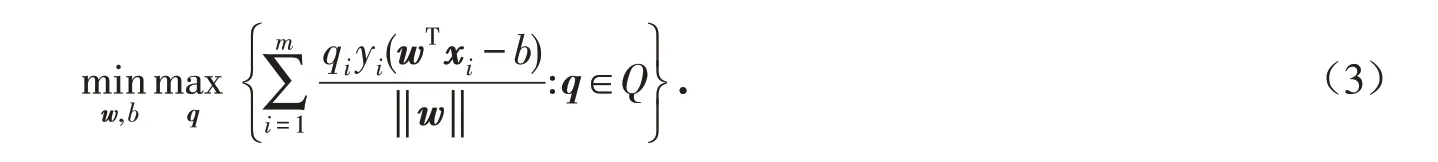
再由Charnes-Cooper变换，可将（3）式改写成（4）式：

3.2 基于谱风险度量的SVM模型

由上述可知，谱风险度量是一致风险度量，所以只需给出Q谱风险的具体形式，就可以将（4）式改写为基于谱风险度量的SVM模型.

为了求出Q谱风险的具体形式，首先写出谱风险度量的辅助函数变形形式：

使用拉格朗日乘子法：

对变量求导有：

由上式知：

得：

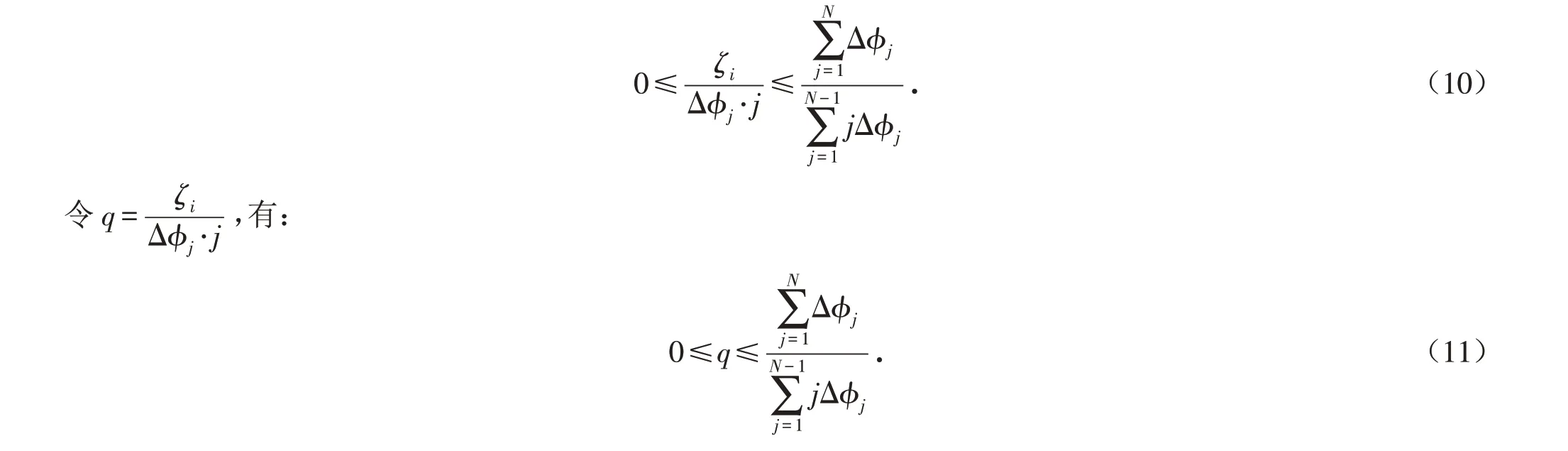
那么Q谱风险的表示形式为：

那么基于谱风险的SVM模型的具体表达式为：

当上式范数的限制条件取1-范数时，是一种非凸的情况，为了解决非凸问题所带来的计算困难，可以将上式限制条件改写为‖w‖ ≤1形式：

从而可以使用凸优化方法求解该模型.

3.3 基于谱风险度量的SVM模型可求解性分析

定理3.1 若（13）式的最优值为负，则（14）式中任意满足w≠0 的最优解对于（13）式也是最优的；若（13）式的最优值为正，则（14）式有一个无意义的解.

下面考虑问题（13）最优值为正的情况，由问题（14）知，若满足问题（14）的解为正值，则唯一满足的解为（0，0），是个无意义的解. 这是因为问题（14）总有一个目标值为非正的可行解，要保证问题（13）最优值为正的情况下，唯一解只能为（0，0）. 证明完毕.

对于其他情形，可以参照Gotoh 等［4］提出的引入正则化范数的方法. 引入l1正则化范数，可以将非凸优化问题转化为一个凸优化问题. 将问题（13）‖w‖ =1 的限制改为线性不等式的形式：w=1，w≥0 即可. 即：

通过问题（16）可以转化成一个凸优化问题，从而求出最优解.

3.4 基于谱风险度量的SVM模型求解算法

为了更加清楚地对基于谱风险度量的SVM模型进行求解，下面给出该模型算法具体的求解步骤：

4 实证分析

ROC曲线越靠近左上角，试验分类的准确性就越高；AUC值表示误分率，即ROC曲线下的面积主要用于衡量模型的泛化性能，即分类效果的好坏，数值越接近1，则表示分类效果越好.

K=1时，分类效果和ROC曲线以及AUC数值如图1、图2所示.

图1 K=1时，分类对比图Fig.1 Classification comparison graph when K=1

图2 K=1时，ROC曲线、AUC数值Fig.2 ROC curve and AUC value when K=1

得到基于CVaR的SVM和基于SRM的SVM的AUC数值分别为0.356、0.740.

K=2时，分类效果和ROC曲线以及AUC数值如图3、图4所示.

图3 K=2时，分类对比图Fig.3 Classification comparison graph when K=2

图4 K=2时，ROC曲线、AUC数值Fig.4 ROC curve and AUC value when K=2

得到基于CVaR的SVM和基于SRM的SVM的AUC数值分别为0.527、0.944.

K=3时，分类效果和ROC曲线以及AUC数值如图5、图6所示.

图5 K=3时，分类对比图Fig.5 Classification comparison graph when K=3

图6 K=3时，ROC曲线、AUC数值Fig.6 ROC curve and AUC value when K=3

得到基于CVaR的SVM和基于SRM的SVM的AUC数值分别为0.418、0.938.

K=4时，分类效果和ROC曲线以及AUC数值如图7、图8所示.

图7 K=4时，分类对比图Fig.7 Classification comparison graph when K=4

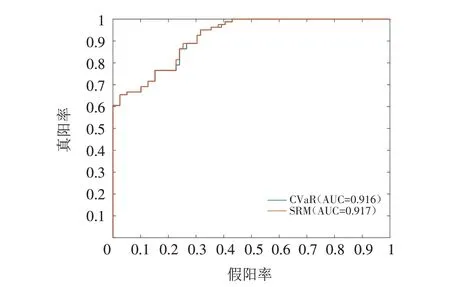
图8 K=4时，ROC曲线、AUC数值Fig.8 ROC curve and AUC value when K=4

得到基于CVaR的SVM和基于SRM的SVM的AUC数值分别为0.916、0.917.

K=5时，分类效果和ROC曲线以及AUC数值如图9、图10所示.

图9 K=5时，分类对比图Fig.9 Classification comparison graph when K=5

图10 K=5时，ROC曲线、AUC数值Fig.10 ROC curve and AUC value when K=5

得到基于CVaR的SVM和基于SRM的SVM的AUC数值分别为0.423、0.444.

由上述实验结果可以看出，使用谱风险度量的SVM模型分类效果基本良好，其ROC曲线都在基于CVaR的SVM 曲线上方，并且基于谱风险度量的SVM 的AUC 数值都要高于基于CVaR 的SVM 的AUC 数值. 通过使用K-folder 交叉验证，得到谱风险的SVM 模型的平均误分率（MSR）为0.3，而基于CVaR 的SVM 模型平均误分率为0.365，比谱风险度量模型的平均误分率高（表1）.

表1 AUC、MSR数值表Tab.1 AUC，MSR value table

对比上述分类效果图、ROC 曲线、AUC 数值和MSR 数值可知，使用谱风险度量的SVM 模型效果比使用CVaR的SVM模型分类效果好，并且谱风险度量的SVM模型的平均误分率比CVaR的低，这在实际应用中有更加精确的分类精度.

5 结论

本文主要利用谱风险度量构造SVM模型来解决分类问题，提升分类精度. 传统的SVM模型受参数影响限制太多，本文通过数值实验使用基于谱风险度量的SVM模型与传统的基于CVaR 的SVM 模型进行对比，这是由于目前使用的CVaR based-SVM只采用了单一的风险权重，并不能真实反映投资者对待风险的态度.所以通过引入谱风险函数，将风险度量扩展到一大类的风险度量. 谱风险度量引用了不同的风险权重，是CVaR的加权和，它的训练模型通过使用辅助函数可以表述成一个凸优化问题，这个问题在计算上很容易处理. 使用谱风险度量在分类中有两个明显的优势：第一，它引用了不同风险权重的CVaR加权和，充分考虑了不同投资者对待风险的态度，更加符合实际情况；第二，它的分类效果要比CVaR的分类效果好，并且平均误分率要比CVaR模型的平均误分率低，提高了分类的精准度.