Relativistic motion on Gaussian quantum steering for two-mode localized Gaussian states
Xiao-Long Gong(龚小龙) Shuo Cao(曹硕) Yue Fang(方越) and Tong-Hua Liu(刘统华)
1School of Physics and Optoelectronic,Yangtze University,Jingzhou 434023,China
2Department of Astronomy,Beijing Normal University,Beijing 100875,China
3Advanced Institute of Natural Sciences,Beijing Normal University at Zhuhai,Zhuhai 519087,China
Keywords: relativistic quantum information,quantum nonlocality,Unruh effect
1. Introduction
Quantum physics, one of the most important scientific achievements in the past years, has fantastic properties that distinguish it from classical physics. One of these fantastic features is the well-known EPR paradox firstly proposed by Einstein, Podolsky, and Rosen (EPR) in 1935,[1]which was subsequently followed by the illustration of the concept of quantum steering in the same year.[2,3]Quantum steering,an intermediate type of quantum correlation between quantum entanglement and Bell nonlocality, is also recognized as the nonlocal quantum correlation (i.e., Alice allows to steer the state of a distant party Bob through local measurements). Actually, many important results have been obtained in the past few years,focusing on the experimental applications of quantum steering. For instance, considering the inherent asymmetric features of EPR steering, its potential applications in the one-side device-independent quantum key distribution is highly emphasized.[4]The asymmetry of quantum steering in different quantum systems has also attracted worldwide attention,with the generation of various theoretical works[5–13]and experimental demonstrations.[14–26]Moreover, a significant amount of work has been done to develop quantum steering characterization and quantification in non-relativistic quantum mechanics, in particular for the Gaussian state. However, it should be pointed out that these works considered only the inertial coordinate system, which indicates the necessity of taking relativistic effects into account in realistic non-inertial coordinate systems. Such conclusion is strongly supported by the recent work,[27]which demonstrates that the Gaussian quantum steering between the Earth and satellites will be strongly affected by the curved space-time around the Earth.
On the other hand,when one part of a multi-body system is involved in relativistic effects, the Unruh effect[28]should be taken into consideration. The traditional method to solve the quantum field mode of scalar or spinor fields(which corresponds to Klein–Gordon or Dirac fields,respectively)is the so-called single mode approximation method,which has been widely used in quantum information tasks quantifying how uniform acceleration affects quantum resources. From theoretical point of view, many efforts have been made to understand quantum systems under different relativistic settings,e.g., the dynamics of quantum steering under the influence of dynamical Casimir effect,[29]the Hawking radiation,[30]and accelerated motions.[31]More related work on relativistic quantum information can be found in the literature.[32–41]In addition,some attempts have previously been made to perform experimental tests of quantum resources in relativistic coordinate systems,with the realization of photonic entanglement in an accelerated setting.[42]However, it is well known that one cannot get the full information from a global mode in the experiment, since the method of single mode approximation is delocalized in practice.[43]Such issue has been extensively discussed in several recent works, taking gravitational or accelerational field as lossy channel rather than global free models, and furthermore calculating the fidelity of the lossy channels.[27,44]Draganet al.[45,46]proposed a new idea,localized mode,to successfully realize the localization of Gaussian states,by storing the squeezed Gaussian states in a simulated cavity capable of transport quantum states. In this case,more attention has been paid to the dynamics of quantum entanglement in localized Gaussian state, with the recent findings that the quantum entanglement increases with the observer’s proper acceleration, but decreases with the width of cavity and central frequency.[47]However, quantum steering in relativistic coordinate system by using localized Gaussian state is still an uncharted territory. In this work, we will study the quantum steering with localized two-mode Gaussian quantum states in relativistic coordinate system. Since the quantification of Gaussian quantum steering has explicit definition,it can be straightly applied to arbitrary two-mode Gaussian states. More specifically, we consider a two-mode squeezed vacuum state with squeezing parameterrof two localized wave packets as input state,and transform it to an accelerated frame of reference corresponding to a pair of uniformly accelerated observers(named Alice and Bob). In the framework of two cases,i.e.,Alice shares the equal or unequal acceleration with Bob,we will show how the observer’s proper acceleration affects the Gaussian quantum steering.
This paper is organized as follows: In Section 2, we briefly describe the localization process of quantum states and select the input state. In Section 3, we introduce the definition and measurements of a bipartite Gaussian quantum steering. The dynamics of Gaussian quantum steering in accelerated coordinate systems are presented in Section 4. Finally,we summarize our conclusions in Section 5. The natural unitsG=c=¯h=kB=1 are employed throughout the paper.
2. The localization process of quantum states
The localization process of quantum states is equivalent to a noisy Gaussian channel,which can be characterized by explicit analytic expressions with no approximations. Moreover,it will not be constrained to the geometry of the Rindler chart,which enables observers to have arbitrary proper accelerations and the minimal distance between them. In this section, we will briefly introduce the noisy quantum Gaussian channel(a detailed description could be found in Section II of Ref.[47]).
2.1. The Gaussian channel
For a real scalar quantum field ˆΦwith a massmin(1+1)-dimensional Minkowski spacetime, its evolution is governed by the Klein–Gordon equation (□+m2) ˆΦ=0, where □=ημν∂μ∂ν. The implicit Klein–Gordan scalar product can be written as

In this paper,we will investigate the scenario in which all modesφkof the Minkowski frame decomposition are empty except for the two modesφIandφIIwith their corresponding annihilation operators ˆfIand ˆfIIin an arbitrary quantum state.Out of the set of accelerated modes, we restrict our attention to two modesψIandψII. Althoughψk/={I,II}are not empty,we just consider two uniformly accelerating observers corresponding toψIandψII,therefore we choose discard the other modes. Our goal is to perform such Gaussian channel to transform the state ofφIandφIIinto the state ofψIandψII.
In order to do this,we introduce the quadrature operators associated withφΛ(Λ ∈{I,II})




whereMandN=NTare 4×4 real matrices. We note that the matrixNdenotes the noise in the quantum channel,whileMis symplectic,[50]whose specification uniquely characterizes the channel. It means that we only need to calculate two matricesMandN.
For convenience,we denoteαI=(ψI,φI),βI=-(ψI,φ⋆I),αII=(ψII,φII) andβII=-(ψII,φ⋆II), then we can obtain the matrixM,which is


2.2. Gaussian wave packet in accelerated coordinates
In general,a photon can be modeled by a wave packet of excitations of a bosonic field.[52]In order to achieve the real scalar quantum field with the relativistic effect, we first focus on the photon wave packet in rest frames,and then extend it to in accelerated coordinates. Here we adopt the following form of the wave packets which are approximately localized and consist of only positive frequency in respective rest frames. This wave packet form has been widely discussed in Refs.[45–47,53]. The input mode consists of a Gaussian develop and sinusoidal modulation as



and|x0|=1/AΛ. Furthermore, we need to make sure that the proper accelerationAΛsatisfies the boundary condition 1/AΛ ≫Ldue to the fact that the accelerating mode functionsψΛare far from the event horizon compared to their sizeL. In Fig.1,we plot the shape of the localized wave packets,with fixed valuesL=2,Ω0≈5,AI=AII=0.1 and the field massm=0.1(just to show the properties of the wave packet).

Fig.1. The shape of input and output modes. We fixed AI=AII=0.1,L=2,Ω0 ≈5,and the field mass m=0.1.
In fact, all the units of these parameters (e.g., accelerationA, lengthLand central frequencyΩ0) can not be chosen until the geometry of the cavity is completely determined.One of the reference is the imaginary cavity in Ref. [56], the lengthLand the travel timeWwere set in order of tens cm and 10-7s, respectively, and the accelerations were accordingly calculated as in order of 1033ms-2. The mode transforms from Minkowski to Rindle spacetime through Bogoliubov coefficient (see Appendix A for more detailed calculations). From the Bogoliubov coefficientαΛ=(ψΛ,φΛ), one can clearly see thatαΛis inversely proportional toAΛwith the mode functions from Eqs.(11)and(13). As shown in Fig.2,with the increase ofAΛ,αΛdecreases monotonically, which also means that the noise in the channel increases.

Fig.2. The relationship between αΛ and AΛ,with L=2,Ω0 ≈5 and the field mass m=0.1.
3. The measurement of Gaussian quantum steering


4. The influence of accelerated effect on localized Gaussian states
We begin with a two-mode squeezed vacuum state characterized only by the squeezing parameterras input state and the covariance matrix


Here we consider two different cases.
Symmetric case In this case, the proper accelerations of two accelerating observers have the same magnitude, i.e.,αI=αII. It is clear that the output stateσ(d)is a symmetric state,also a state with balanced correlations.
Asymmetric case The two accelerating observers have unequal-magnitude proper acceleration, i.e.,αI/=αII. Although the output stateσ(d)is no longer symmetric,it is still a balanced-correlated state.
For convenience, we useAΛto replaceαΛ.αΛ= 1 andAΛ=0 mean that the proper acceleration equals to zero,whereAΛis proportional to acceleration(please refer to Fig.2 for more details).
We first focus on the symmetric case. In this case, the Gaussian quantum steering fromA →BandB →Ais equivalence,which means thatGA→B=GB→Awith the symmetrical property. The numerically computed Gaussian steering with increased acceleration parametersAIandAIIin this case are plotted in Fig.3. We can see thatGA→BandGB→Aboth monotonically decreases with the increase of accelerated parametersAI=AIIof observes Alice and Bob. This findings demonstrate that the Unruh effect will affect the Gaussian quantum steering and decrease it, which is consist with previous works.[27,28,44]Our results also indicate that, when performing more reliable quantum steering tasks, the relativistic effects cannot be ignored.

Fig. 3. The Gaussian quantum steering GA→B and GB→A between observers Alice and Bob(corresponding to wave packets ψI and ψII)moving with equal-magnitude accelerations AI=AII=A are shown. The original state is a two-mode squeezed vacuum state characterized by a squeezing parameter r=1 of the inertial wave packets φI and φII.

Fig. 4. The contour plot GA→B as a function of accelerated parameter AI (AI=AII)and squeezing parameter r.
In Fig. 4, we plotGA→Bas a function of accelerated parameterAIand squeezing parameterr. We can observe a monotonic increase ofGA→Bwith the increasing of the squeezing parameterr. It should be noted that, comparing with the accelerated parameter, the Gaussian steeringGA→Bchanges more for different squeezing parameters,which indicates that the initial quantum resource plays a more important role in the quantum steering. In other words,comparing with the squeezing parameter,the Gaussian steering is not easy to change with changing accelerated parameter. This gives us the guidance to choose appropriate physical parameters to perform more reliable quantum steering tasks with the inevitable relativistic effects.
Subsequently, we turn our attention to the asymmetric case. We plot the Gaussian quantum steeringGA→BandGB→Aas the functions of the Alice’s acceleration and Bob’s acceleration for fixed squeezing parameterr=3 in Fig 5. From this figure,we can see that,both theGA→BandGB→Awill decrease with the increase of accelerated parameters. In additional,the Gaussian quantum steering degradation is inevitable since the mode mismatch between input and output modes cannot be removed by any amendments to the protocol.[46,47]Moreover,whenAI=AII, it corresponds to the symmetric case. WhenAI/=AII, it corresponds to the asymmetric case, which indicates that the asymmetric properties of Gaussian quantum steering will arise. To check the asymmetric degree of steerability by using local mode with relativistic effects,we calculate the Gaussian steering asymmetry and plot it as a function of accelerated parameterAIfor different squeezing parameterrin Fig. 6. This allows us to have a better understanding of how the relativistic motions and the squeezing parameter of initial quantum state affect steering asymmetry. This figure clearly shows that the Gaussian steering asymmetry increase for a specific range of accelerated parameter, and then gradually approach to a finite value with increasingAI. This is because that the Unruh effect almost completely destroys the one-side Gaussian quantum steeringGA→Bwhich means that one can no longer measure Alice to manipulate Bob.More importantly, we can see that the different squeezing parameters will change the inflection point,i.e.,the smaller the squeezing parameter, the earlier the inflection point. This is reasonable,since the squeezing parameters of the initial state determine the quantization of the quantum resource.

Fig. 5. The Gaussian quantum steering GA→B (red) and GB→A (gray)as the functions of the Alice’s acceleration and Bob’s acceleration for fixed squeezing parameter r=3.
Due to the Gaussian quantum steering asymmetry effect is arising,it is natural to wonder if this situation is caused by a mismatch of modules. In order to visualize Gaussian quantum steering asymmetry effect, we randomly generated 2000 sets ofσ(d)with different values ofAI,AII∈[0.005,0.25]andr ∈[1,3]. We now simply define the asymmetry asPasy:=log2(AI-AII). As shown in Fig.7,we numerically computed the differential Gaussian quantum steeringGB→A-GA→Band marked it in cold/warm colors according to their values, and the specific color-value correlation can be found in colorbar.For convenience, we have plotted the dashed vertical linePasy=0,and the closer the dots are to the dashed vertical line,the lower the asymmetry. All the cool colored dots, i.e., the states withGB→A >GA→B,form an interesting chimney shape,while the other warm dots are concentrated in the upper left and upper right regions. It is also shown that no matter how muchrincreases,as long as the asymmetry stays within a certain range(about[-0.2,0.2]here).As the final remark,we can conclude that the arising of Gaussian quantum steering asymmetry effect is not caused by a mismatch of modules.

Fig. 6. The Gaussian quantum steering asymmetric GA→B-GB→A as a function of the Alice’s acceleration for different squeezing parameter,r=0.8 (red dashed line), r=0.9 (black dashed line) and r=1 (blue dashed line),respectively. The Bob’s acceleration is fixed as AII=0.

Fig.7. The differential differential Gaussian quantum steering GB→AGA→B versus the corresponding value of squeezing parameter r and asymmetry Pasy,which defined as Pasy:=log2(AI-AII),for randomly generated states. The closer the dots are to the dashed vertical line,the higher the symmetry.
5. Conclusions
In this paper, we have studied Gaussian steering by using local mode instead of traditional single-mode approximation method in relativistic frame. We firstly considered two uniformly accelerating observers,Alice and Bob,which transform a two-mode squeezed vacuum state prepared in an inertial frame from the initial frame to the frame of the observers,and this behavior can be represented as a Gaussian quantum channel. We obtained a simplified form of the channel and can use it to easily compute the output state.
Within the framework introduced there, we analyzed the Gaussian quantum steering and its asymmetry that can be extracted from the input two-mode squeezed vacuum state. We have shown that one-side Gaussian quantum steering monotonically decreases with increasing observers of acceleration.The findings demonstrate that the Unruh effect will affect the Gaussian quantum steering. In addition, the Gaussian quantum steering degradation is inevitable since the mode mismatch between the input and output modes cannot be removed by any amendments to the protocol. Our results also indicate that, when performing more reliable quantum steering tasks,the relativistic effects cannot be ignored. Comparing with the squeezing parameter, the Gaussian steering is not easy to change with changing accelerated parameter. This gives us the guidance to choose appropriate physical parameters to perform more reliable quantum steering tasks with the inevitable relativistic effects. Finally, we have shown that the Gaussian steering asymmetry increase for a specific range of accelerated parameter, and then gradually approach to a finite value with increasing observer’s acceleration. This is because the Unruh effect almost completely destroys the one-side Gaussian quantum steering which means that one can no longer measure Alice to manipulate Bob.
As the final remark, although the influence of Unruh effect on quantum steering cannot be detected by current technology, it on quantum steering or other quantum resources cannot be ignored, especially when performing relativistic quantum information tasks.
In addition,according to the equivalence principle,the effects of acceleration are equivalence with the effects of gravity, our results could be in principle applied to dynamics of Gaussian steering between the Earth and satellites. Since realistic quantum systems will always exhibit gravitational and relativistic features, our results should be significant both for giving pieces of advices to realize quantum information protocols such as quantum key distribution from the Earth to satellites and for a general understanding of quantum steering in relativistic quantum systems.
Appendix: Bogoliubov coefficients calculation
In the Minkowski coordinates, the Klein–Gordan equation could be solved in the form of the normalized plane waves
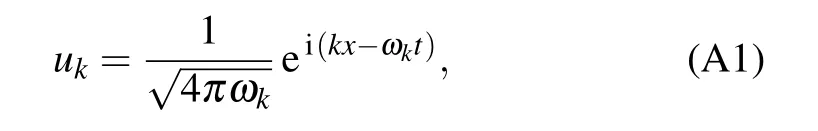
Acknowledgements
Project supported by National Key R&D Program of China (Grant No. 2017YFA0402600); the National Natural Science Foundation of China (Grant Nos. 11690023,11373014, and 11633001); Beijing Talents Fund of Organization Department of Beijing Municipal Committee of the CPC;the Strategic Priority Research Program of the Chinese Academy of Sciences(Grant No. XDB23000000);and the Interdiscipline Research Funds of Beijing Normal University.
- Chinese Physics B的其它文章
- A nonlocal Boussinesq equation: Multiple-soliton solutions and symmetry analysis
- Correlation and trust mechanism-based rumor propagation model in complex social networks
- Gauss quadrature based finite temperature Lanczos method
- Experimental realization of quantum controlled teleportation of arbitrary two-qubit state via a five-qubit entangled state
- Self-error-rejecting multipartite entanglement purification for electron systems assisted by quantum-dot spins in optical microcavities
- Pseudospin symmetric solutions of the Dirac equation with the modified Rosen–Morse potential using Nikiforov–Uvarov method and supersymmetric quantum mechanics approach

