例谈构造函数在导数解题中的应用

■江苏省宿豫中学 罗伟

导数是高考命题的热点和难点之一,可以利用导数来证明不等式、求参数的取值范围、探究函数的零点等问题,命制的题目具有结果独特、综合性强等特点,而构造函数是解决导数问题的基本方法,如何合理地构造函数是解题的关键,下面举例谈谈构造函数的一些常用方法。

题型一、构造可导的积的形式函数

例1已知函数y=f(x)的图像关于y轴对称,且当x∈(-∞,0)时,f(x)+xf＇(x)＜0 成立,a=20.2·f(20.2),b=logπ3·f(logπ3),c=log39·f(log39),则a,b,c的大小关系为()。

A.a＞b＞cB.a＞c＞b

C.c＞b＞aD.b＞a＞c

解析:因为函数y=f(x)关于y轴对称,所以函数y=xf(x)为奇函数。因为[xf(x)]＇=f(x)+xf＇(x),所以当x∈(-∞,0)时,[xf(x)]＇=f(x)+xf＇(x)＜0,函数y=xf(x)单调递减;当x∈(0,+∞)时,函数y=xf(x)单调递增。因为1＜20.2＜2,0＜logπ3＜1,log39=2,所以0＜logπ3＜20.2＜log39,所以b＞a＞c。故选D。

点评:如果题设条件满足结构f＇(x)g(x)+f(x)g＇(x),可以构造函数h(x)=f(x)g(x)。例如:(1)对于f＇(x)+f(x)＞0(＜0),可构造函数h(x)=ex·f(x);(2)对于xf＇(x)+f(x)＞0(＜0),可构造函数h(x)=x·f(x);(3)对于xf＇(x)+nf(x)＞0(＜0),可构造函数h(x)=xn·f(x)等。

题型二、构造可导的商的形式函数

例2已知定义在R 上的可导函数f(x)的导函数为f＇(x),若对于任意实数x,有f(x)＞f＇(x),且y=f(x)-1为奇函数,则不等式f(x)＜ex的解集为()。

A.(-∞,0)B.(0,+∞)

C.(-∞,e4)D.(e4,+∞)

解析:因为y=f(x)-1为奇函数,且定义域为R,所以f(0)-1=0,得f(0)=1。设h(x)=,则h＇(x)=,因为f(x)＞f＇(x),所以h＇(x)＜0,所以h(x)是R 上的减函数,所以不等式f(x)＜ex等价于,所以x＞0。故选B。

题型三、对局部进行构造函数

例3已知函数f(x)=,若x0＜1,设直线y=g(x)为函数f(x)的图像在x=x0处的切线,求证:f(x)≤g(x)。

证明:函数f(x)的图像在x=x0处的切线方程为y=g(x)=f＇(x0)(x-x0)+f(x0)。

令h(x)=f(x)-g(x)=f(x)-f＇(x0)(x-x0)+f(x0),x∈R,则h＇(x)=f＇(x)-f＇(x0)=。

设φ(x)=-(1-x0)ex,x∈R,则φ＇(x)=-(1-x0)ex。

因为x0＜1,所以φ＇(x)＜0,所以φ(x)在R 上单调递减。

因为φ(x0)=0,所以当x＜x0时,φ(x)＞0,h＇(x)＞0;当x＞x0时,φ(x)＜0,h＇(x)＜0。

所以h(x)在区间(-∞,x0)上为增函数,在区间(x0,+∞)上为减函数,故x∈R时,h(x)≤h(x0)=0,故f(x)≤g(x)。

点评:对于一类不等式的证明或求参数问题,若直接构造函数无法解决,则我们可以将问题转化为构造函数h(x)=f(x)·g(x)或,其中f(x)与g(x)某一个函数可明显判断出与零的大小关系,则另外一个函数即为构造对象,可以简化解题过程,顺利解决问题。

题型四、先放缩再构造函数

例4设函数f(x)=ln(x+1)++ax+b(a,b∈R,a,b为常数),曲线y=f(x)与直线y=在点(0,0)处相切。

(1)求a,b的值;

(2)求证:当0＜x＜2时,f(x)＜。

解析:(1)a=0,b=-1。(过程略)

(2)当x＞0 时,由均值不等式得＜x+2,故+1。

所以f(x)=ln(x+1)+-1＜ln(x+1)+。

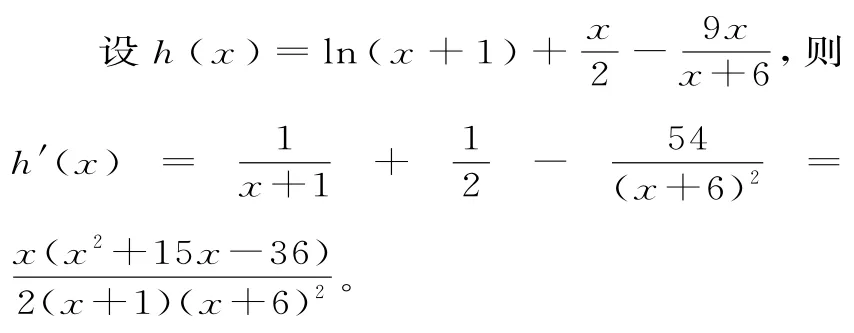
当0＜x＜2时,h＇(x)＜0,所以h(x)在(0,2)内是减函数。

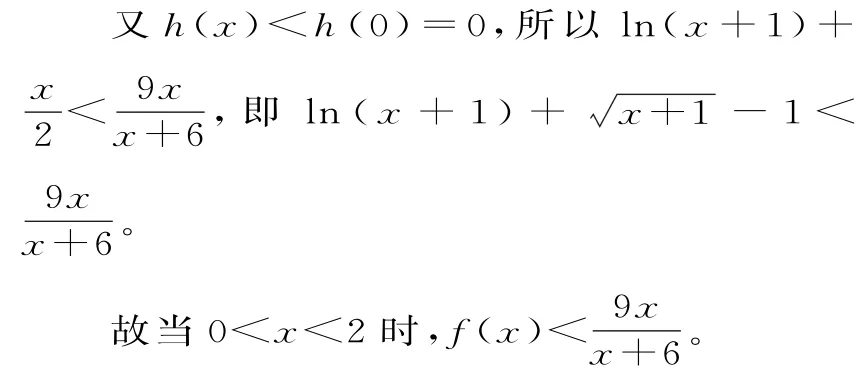
点评:若待求的函数式较为复杂时,可利用函数的单调性、基本不等式、已成立的不等式等将函数式的一部分进行放缩,然后再构造函数,这样可以获得事半功倍的效果。例如:要证f(x)＜g(x)⇔f(x)＜h(x)(新构造的函数)＜g(x);或f(x)＞g(x)⇔f(x)＞h(x)(新构造的函数)＞g(x)。

题型五、变形后再构造函数

例5已知函数f(x)=kx,g(x)=,若不等式f(x)≥g(x)在区间(0,+∞)上恒成立,求实数k的取值范围。

解析:f(x)≥g(x)在区间(0,+∞)上恒成立,即kx2-lnx≥0在区间(0,+∞)上恒成立,令h(x)=kx2-lnx(x＞0),则h＇(x)=。

(1)若k≤0,显然h(x)≥0不恒成立。

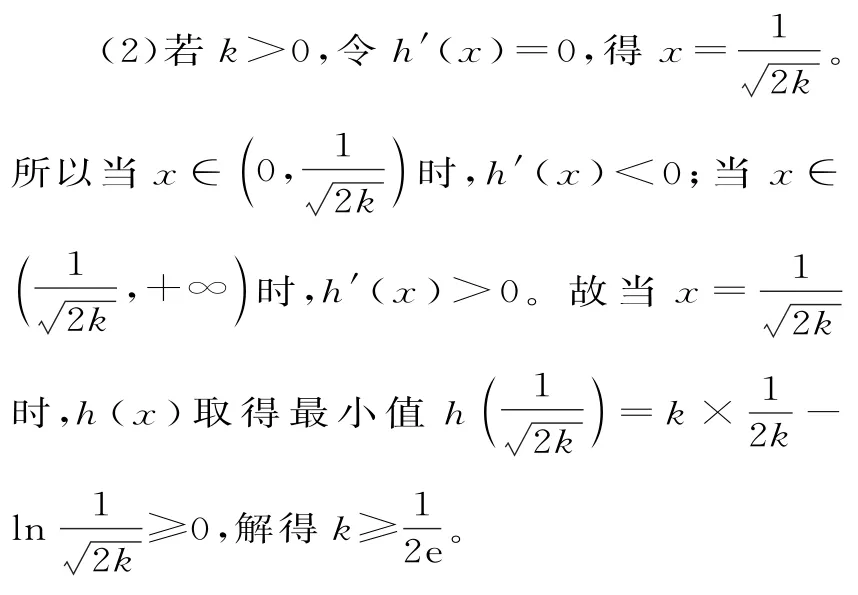
点评:对于一类指数式的不等式,可以先对不等式两边取对数,进行等价转化,使函数式得以化简,再构造函数;或者对主元的结构形式进行换元,将分式化为整式进行换元,这样可以简化构造的函数。例如:本题如果直接构造函数h(x)=kx-,极值点不能具体求出,需要整体代换,过程相对复杂,没有上述方法简洁易行。