QMC方法在数量金融中的新挑战分析

赵倩

摘要：在新时期环境下，我国金融领域的发展十分迅速，而在金融领域的发展中产生了多样化的金融产品，而在金融工作开展中往往面临诸多的金融问题，为了实现对此类问题的解决，金融模型的应用十分重要，但因为金融模型存在复杂性，对很多的金融问题都不能有效解决，而QMC作为一种广泛使用的方法也在数量金融中存在着诸多挑战。文章就主要针对QMC方法在数量金融中的新挑战进行分析，希望对相关工作的研究提供参考。

关键词：QMC方法;金融领域;数量金融;金融问题

在如今金融市场中，具有复杂性的特点，为了促进其能够有效发展，需要使用到大量个性化的金融工具，而金融模型则是对金融情况刻画的重要手段。由于金融模型在建立中呈现出显著复杂性特点，且易受到诸多因素的影响，使大量金融方面的问题并不可以得到显式的求解，而QMC方法就是一种对复杂性金融问题解决的数值方法，但此方法在使用中还存在诸多的难题需要克服，而这就是本文主要研究的内容。

一、QMC方法概述

通过传统数值的积分法并不能够对高维积分问题解决，且要被积的函数还需要在光滑性方面符合要求，如梯形法使用中要求其被积函数的二阶导数要在连续性方面呈现一定条件，而辛普森的法则要求其被积函数的四阶导数要具有良好连续性。对于很多金融的问题来说，其目标函数在光滑性方面一般都不满足条件，且维数也往往很高，所以在对传统数值的积分法使用中，不能保证使用的效果，但MC方法则能够实现对此类困难的克服。此MC方法公式为：

在上式中，只要相应的积分存在，可通过强大数的定律获取：

这说明I^n（f）为I（f）强结合的估计，且说明MC的方法具有十分广泛适用范围，进一步若存在I（f2），则I^n（f）估计量均方根的误差是：

在上式内，σ2=I（f2）-I（f）2，表明了此MC 方法于概率意义误差中具有O（n-1/2）收敛阶，并不对维数d产生依赖。若d>4的话，此MC方法具有收敛的速度比梯形法则收敛速度要快。若d>8，此MC方法的收敛速度比辛普森的法则收敛速度要快。尽管MC方法可以对维数的灾难等相关问题实现有效克服，但同样其还存在一定的缺陷需要解决，主要体现在它只存在概率意义中误差界，和传统数值积分存在确定误差界不一样;它对全部类型被积的函数，不管此函数是不是光滑，此MC方法具有一样的收敛阶，当面对一些呈现出更加光滑特性的函数，使用此MC方法不能得到更高收敛阶，若使用传统数值的积分就能够满足要求;计算机对理想化随机点列很难生成，往往只能对伪随机的点列生成。

二、高维和间断对QMC方法产生的影响

（一）高维对QMC方法产生的影响

大量金融问题的维数都会超过上千的情况，比较常见的有期权定价的问题等，基于QMC法O（n-1（log n）d）收敛阶分析，此QMC法是不利于对高维问题解决的，这主要是即使对较为适中性维数来说，此QMC法其收敛阶中（log n）d对数项亦可能十分大。如d=8时，想要达到n-1（log n）d<n-1/2的情况，要求n不低于1029×1.79，而实际中此数量级样本量很难得到实现。但通过众多的实证研究得知，即使金融问题达到数百维，此QMC的方法还是比MC的方法要优越得多，面对此种情况，很多学者也进行了合理解释。

一些学者阐述了在对一些加权的函数类中，以QMC法对其维数灾难的相关问题实现有效解决;还存在一种解释则是基于有效维数概念的。一些学者发现在诸多高维的金融问题中存在较低有效的维数，在加入函数 f后可以对其写成两部分的内容，也就是 fL和 fH，且fL与fH呈现出正交的关系，且fH具有的方差其实只占到f方差极小的比例，fL维数是有效的维数。因为一维投影是低偏差的序列，和前几维的投影比其随机序列具有更好均匀性，但其后几维的投影存在均匀性的不理想，所以当存在较小的有效维数时，此QMC的方法能够对fL很好处理，也许它并不能够对 fH很好处理，但此函数并不会对整体的误差存在较大贡献，这也就说明了 QMC的方法为什么能够对低有效的维数金融问题成功处理。

因为QMC的方法效率遭受维数影响，大量研究尝试借助减小有效的维数对QMC效率提升。尤其对金融的问题，通过合适路径模拟法能够对问题有效维数减小。在一些研究中，表明了一些路径的模拟法比标准路径的模拟法存在更好表现效果，如布朗桥方法和主成分的分析方法等，但它们都存在相同缺陷，其并非对目标的函数特征实施充分考虑，则它们的效率还是对问题实际特性产生依赖。

（二）间断对QMC方法产生的影响分析

上文所提路径的模拟方法，只是出于对有效维数减小的目的，同时目标函数具有的光滑性同样对QMC的方法效率产生制约。在一些研究中，面对不连续的函数提出一种OT法（正交变换法），这也表明路径模拟法实现对间断性的特征显著的影响，且还通过对一类路径的模拟法设计，让间断的结构产生对QMC法的“友好性”。

面对诸多的金融问题，如期权定价以及Greeks计算等，涉及一个或多个数量不光滑结构，对他们主要进行两种常见类型的归纳，一种是间断结构，表示为I{ψ≥0}，还有一种是折褶结构，表示为max（ψ（x），0），且ψ（x）代表Rd中连续性的函数，此研究表明了目标函数具有不光滑性对QMC法效率产生了影响。一些研究中提出QMC法的性能发生退化现象，主要是因为被积的函数自身呈现间断点或者在光滑性方面存在不足而造成的;还在一些研究中观察出，折褶的结构通过ANOVA的分解会呈现出光滑的低阶项情况，且其光滑性会对路径模拟法的使用较为依赖。对金融的应用方面，一些研究使用路径模拟法对间断结构改变，从而获取QMC的友好型间断点;一些研究中對相关数值分析结果表明，对变换后间断结构来说，此QMC法效率得到了显著的提升，但在研究中还普遍存在方法局限性的问题，往往只对单个间断的结构目标函数实施考虑，并未结合多个间断的结构以及多个的折褶结构，实现全面考虑与综合分析，而这也意味着对具多个数量非光滑的结构奇异期权，此OT方法就得不到有效使用。面对此类缺陷，就需要针对多个数量非光滑的结构设计出一种路径模拟的方法，即QR法。此QR法能够按照非光滑的结构重要性实施变换，让比较重要非光滑的结构对更少变量依赖，提供一种度量、非光滑习惯结构的重要性指标，基于此，可以对此类非光滑的结构重要性实施排序，后变换处理，通过数值结果分析此方式对非光滑的结构变换，能够对QMC的方法效率实现显著提升。

三、QMC方法在数量金融中的降维和间断处理

（一）QMC方法在数量金融中的降维处理

对布朗运动初始生成的矩阵Ao给定，把收益函数进行独立性标准的正态变量写成，表示为z=（z1，...，zd）T～ N（0，Id）的G（z）函数，并用H（A0z）代表。面对任意的正交阵U情况，通过E[G（z）]=B[G（Uz）]能够得知，被积函数对G（z）或者G（Uz）选择具有等价性。对连续光滑性G（z）目标函数考虑，如何找到一个正交的矩阵U让QMC法来对G（Uz）函数的效率实现尽可能提升，是需要重点研究的内容。

如果G（z）被积函数是一线性的函数，则LT方法不断在任意点展开均能够对函数线性的结构抓住，所选择正交阵ULT能够把截断的维数降到1维。但是如果G（z）被积函数是一较为复杂性、非线性的函数，则LT方法于若干个数量给定点展开信息的话，可能并不会对被积函数重要结构很好解释。而对G（z）复杂性被积函数，一些学者提出了一个匹配的策略，也就是对G（z）函数选择某点Taylor的展开式当作G（z）原函数匹配的函数。具体来说，此函数表示为G1（z）=G（zo）+▽G（zo）T（z-z0），zo∈Rd，此函数可当作G（z）函数的匹配性函数。一些学生提出了QR方法，能够直接用在较简单函数G（z），且求得出一个正交的方阵U，让使G1{Uz}截断的维数得到显著降低，把正交的方阵U用在原函数的G（z）中，其效果主要对匹配的函数G（z）和原函数的G（z）中接近程度较为依赖。

（二）QMC方法在数量金融中的间断处理

在对非光滑的结构重要性实施排序和变换后，尽管按照此方式实现非光滑的结构变换，能够有效促进QMC的方法效率提升，但其间断点依然存在。这就说明完成变换的间断性结构还可能对QMC的方法效率产生一定的影响，因此另一种对QMC的方法效率提升的策略是对目标的函数间断点移除。现阶段，诸多光滑化的方法在MC的方法或其他领域中普遍使用。在通过pathwise法对敏感性的参数估算时，其收益函数间断点往往会使此方法发生失效，为了对pathwise法使用，可以通过条件的期望来对此类间断点移除，从而获取一个光滑性无偏的估计;一些研究提出通过对敏感性的参数计算来实现核估计，其能够对含间断点收益函数进行处理，但此核光滑的技术所获取有偏的估计，且实际操作中很难对其估计的误差把握;面对障碍期权的定价问题情况，一些研究在障碍的条件下来对标的的资产演变过程实施条件的抽样，获取一个光滑无偏的估计;一些人员针对亚式的期权提出一种条件的MC法，此种方法以收益函数为基础关于股票的价格几何性平均值条件具有的期望存在闭合的解。关于光滑技术以及路径模拟的方法结合的QMC法是很少的，一些研究根据障碍期权进行一种结合了LT法条件抽样的模式引入，且还把此方法向Heston的模型推广。

通过对诸多方法综合分析，提出一种VPO的光滑化法，并和此光滑化法以及一些路径的模拟法结合，来对带有间断的结构金融问题进行解决。此方法和条件MC的方法存在不同，在本文中所提出VPO的光滑化法不需事先对条件期望计算，但其VPO的光滑化法要求此被积函数间断的结构符合相应条件。对存在的一些金融方面问题，通过设计出合适路径模拟的方法对此类条件满足，但并非全部路径模拟的方法都符合VPO的光滑化法所需条件。为了使此光滑化的方法对常见金融问题适用，就要对QR法实施修正，称作MQR法，此MQR法可以如QR法一样按照间断结构重要性实施处理，且它能够和VPO的光滑化法结合，此两种方法结合可以对间断点消除，且还能够对有效维数双重效果减小。

四、QMC方法在数量金融中的应用分析

（一）普通QMC方法在多期收入的保证价格应用

在多期收入C（0）保证价格中，“多期”主要在数学方面体现出路径的依赖，也就是要求模拟成η（t）整个的路径，此时要对w（t）和N（t）增量的独立性考虑，将T[0，T]时间区间等分作J份，其步长为dt=T/J，表示为0<dt<…<Jdt=T，dW（j）=w（t）-（t-dt）-N（0，dt），生成出dw（j）估计为：dw（j）=，且Z-N（0，1），同理可得dw（j）=、dN（j）=N（t）-N（t-dt）～P（λdt），其中dN（k）=P。在dN（k）的生成中，Pλdt-P（λt）在生成出dW（j）与dN（k）之后，会再生成出InK（1）-N（μ，σ2），后将三个数量随机向相关公式带入，得到C（0）公式内显著性水平α置信的区间。

（二）条件QMC方法在多期收入的保证价格应用

对X目标函数的表达式表示为Xi=（η·（t）-γ）+，进而进一步对E（Xt|Wt），欧式的看涨期权马尔可夫的性质在任意的时刻价格是：

结合标的Sto（t）其服从几何的布朗运动，最终能够得到显著性的水平α置信的区间。

（三）应用结果分析

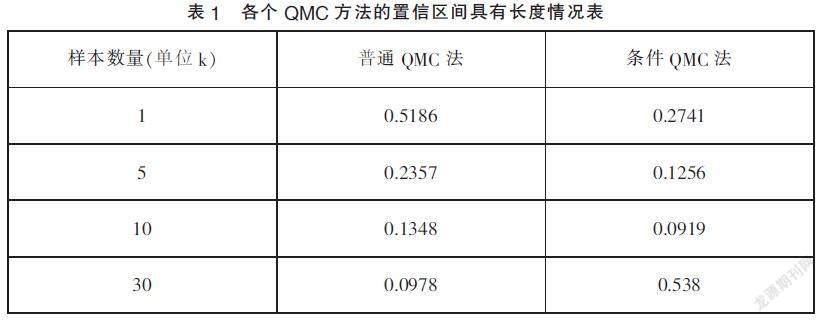
所给定的参数值置信区间的长度几乎不存在区别，但在动态化参数值下，期置信的区间长度情况如表1。

从表1分析可得，普通QMC法具有模拟的精确度是最差的，对偶的变量法及控制的变量法具有相似的精确度，且控制的变量法要略好一点，条件QMC法具有最高的精确度。而之所以出现这样的情况，是因为条件QMC法对条件期望解析解进行使用，数值的解精度即使再高也不可能比解析解更高。但即使有解析解的存在，此条件期望的解析解存在此前提条件也是很难实现的。因此能够看出，得到条件期望解析公式其实并非易事。控制的变量法其难点主要是控制变量的均值解析求解，其复杂的程度是没有QMC法高的，对偶的变量法是最简单的，而精确度只比控制的变量法略差，和普通的QMC法相比有所改善。

对多期收入的保证价格各参数给定，各QMC法都能够对其数值解有效阶段，将显著性的水平是 a=0.05置信区间的长度当作评价的指标，得出普通QMC法置信区间的长度是最大的，对偶的变量法以及控制的变量法稍次之，而条件QMC法是最小的，且普通的QMC法具有最差的精确度，条件QMC法具有最好的精确度。

五、结语

综上所述，在数量金融中QMC方法得到了广泛使用，但在QMC方法的使用中还存在诸多的难题与挑战，常见高维和间断情况，为了确保QMC方法能够有效使用，就需要根据针对其存在的难题与挑战积极进行解决方法的探索，确保其方法效果充分发挥。

参考文献：

[1]孔云波，冯新喜，许丁友，等.基于QMC采样的GMPHD分布式融合方法[J].系统工程与电子技术，2017，08（39）：40-46.

[2]王学祯，王辰，徐敬卿.运用“合同质量管理”模式突破質量管理瓶颈[J].质量春秋，2018（9）：27-32.

[3]韩建宇.在Variance-Gamma模型下结合QMC方法对期权定价[D].北京：清华大学，2017.

[4]张刚，黄南飞，张天骐.PQMC-NRCDSK方案的设计与性能分析[J].西安电子科技大学学报（自然科学版），2020，47（01）：1-9.

[5]刘志东，许健强.基于蒙特卡洛模拟的金融资产价格跳跃非参数检验方法比较研究[J].数量经济技术经济研究，2016，33（03）：128-145.

[6]罗鑫，张金林.基于蒙特卡罗方法的含转股价向下修正条款的可转债定价研究[J].金融理论与实践，2020（10）：45-53.

（作者单位：俄罗斯圣彼得堡理工大学经济学院）